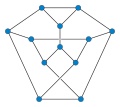
wykres Tietze'a
| Graf Tietze | |
|---|---|
 Graf Tietze
| |
| Wierzchołki | 12 |
| Krawędzie | 18 |
| Promień | 3 |
| Średnica | 3 |
| Obwód | 3 |
| Automorfizmy | 12 ( D 6 ) |
| Liczba chromatyczna | 3 |
| Indeks chromatyczny | 4 |
| Nieruchomości |
Sześcienny Snark |
| Tabela wykresów i parametrów | |
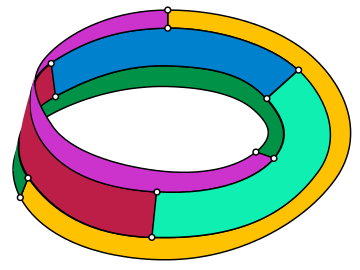
W matematycznej dziedzinie teorii grafów wykres Tietze jest nieskierowanym grafem sześciennym z 12 wierzchołkami i 18 krawędziami. Jej nazwa pochodzi od Heinricha Franza Friedricha Tietze , który wykazał w 1910 r., że wstęgę Möbiusa można podzielić na sześć obszarów, które się stykają – trzy wzdłuż granicy paska i trzy wzdłuż jego linii środkowej – a zatem grafy, które są osadzone na pasku Möbiusa może wymagać sześciu kolorów . Segmenty graniczne regionów podziału Tietze (w tym segmenty wzdłuż granicy samego paska Möbiusa) tworzą osadzenie wykresu Tietze.
Związek z wykresem Petersena
Graf Tietze'a można utworzyć z grafu Petersena , zastępując jeden z jego wierzchołków trójkątem . Podobnie jak wykres Tietze, wykres Petersena tworzy granicę sześciu stykających się ze sobą regionów, ale na płaszczyźnie rzutowej, a nie na pasku Möbiusa. Jeśli wycina się otwór z tego podziału płaszczyzny rzutowej, otaczającego pojedynczy wierzchołek, otoczony wierzchołek zostaje zastąpiony trójkątem granic obszaru wokół otworu, co daje opisaną wcześniej konstrukcję wykresu Tietze.
hamiltonowość
Zarówno wykres Tietze, jak i wykres Petersena są maksymalnie niehamiltonowskie : nie mają cyklu Hamiltona , ale dowolne dwa niesąsiadujące wierzchołki można połączyć ścieżką Hamiltona. Wykres Tietze'a i wykres Petersena to jedyne grafy sześcienne niehamiltonowskie połączone z 2 wierzchołkami , które mają 12 lub mniej wierzchołków.
W przeciwieństwie do wykresu Petersena, wykres Tietze nie jest hipohamiltonowski : usunięcie jednego z jego trzech wierzchołków trójkąta tworzy mniejszy graf, który pozostaje niehamiltonowski.
Kolorystyka krawędzi i doskonałe dopasowanie
Kolorowanie krawędzi Wykres Tietze wymaga czterech kolorów; to znaczy jego indeks chromatyczny wynosi 4. Równoważnie krawędzie wykresu Tietze można podzielić na cztery dopasowania , ale nie mniej.
Wykres Tietze pasuje do części definicji snarka : jest to graf sześcienny bez mostków , którego nie można pokolorować na 3 krawędziach. Jednak większość autorów ogranicza snark do grafów bez 3 cykli, więc graf Tietze nie jest ogólnie uważany za snark. Niemniej jednak jest izomorficzny z grafem J 3 , należącym do nieskończonej rodziny snarków kwiatowych wprowadzonej przez R. Isaacsa w 1975 roku.
W przeciwieństwie do wykresu Petersena, wykres Tietze może być objęty czterema doskonałymi dopasowaniami . Ta właściwość odgrywa kluczową rolę w dowodzie, że testowanie, czy graf można pokryć czterema doskonałymi dopasowaniami, jest NP-zupełne .
Dodatkowe właściwości
Wykres Tietze'a ma liczbę chromatyczną 3, indeks chromatyczny 4, obwód 3 i średnicę 3. Liczba niezależności wynosi 5. Jego grupa automorfizmów ma rząd 12 i jest izomorficzna z grupą dwuścienną D 6 , grupą symetrii sześciokąta , zawierającą oba obroty i odbicia. Ta grupa ma dwie orbity o rozmiarze 3 i jedną o rozmiarze 6 na wierzchołkach, a zatem ten graf nie jest przechodni przez wierzchołki .
Galeria
Liczba chromatyczna wykresu Tietze wynosi 3.
Indeks chromatyczny wykresu Tietze wynosi 4.
Graf Tietze ma numer przecięcia 2 i jest 1-płaszczyznowy .
Zobacz też
- Wykres Dürera i wykres Franklina , dwa inne grafy sześcienne o 12 wierzchołkach