85 sposobów na zawiązanie krawata

85 sposobów na zawiązanie krawata

Autor	Thomasa Finka i Yong Mao
Wydawca	Cztery nieruchomości
Data publikacji	4 listopada 1999
ISBN	1-84115-249-8
OCLC	59397523

The 85 Ways to Tie a Tie to książka Thomasa Finka i Yong Mao o historii wiązanego krawata , nowoczesnego krawata i sposobu wiązania każdego z nich. Opiera się na dwóch artykułach matematycznych opublikowanych przez autorów w Nature i Physica A, gdy byli oni pracownikami naukowymi Cavendish Laboratory na Uniwersytecie Cambridge . Autorzy dowodzą, że przy założeniu typowego rozmiaru krawata i osoby noszącej krawat istnieje dokładnie 85 sposobów wiązania krawata konwencjonalną metodą owijania szerokiego końca krawata wokół wąskiego końca. Opisują każdy z nich i podkreślają te, które uznają za znaczące pod względem historycznym lub estetyczne.

Został opublikowany przez Fourth Estate 4 listopada 1999 r., A następnie opublikowany w dziewięciu innych językach.

Matematyka

Odkrycie wszystkich możliwych sposobów zawiązania krawata zależy od matematycznego sformułowania aktu zawiązania krawata. W swoich artykułach (które mają charakter techniczny) i książce (która jest przeznaczona dla laików, z wyjątkiem dodatku), autorzy pokazują, że węzły krawata są równoważne uporczywym przypadkowym spacerom po trójkątnej siatce, z pewnymi ograniczeniami co do tego, jak spacery się rozpoczynają i koniec. Zatem wyliczenie węzłów krawata n ruchów jest równoważne wyliczeniu spacerów o n krokach. Narzucenie warunków symetrii i równowagi redukuje 85 węzłów do 13 estetycznych.

Reprezentacja węzła

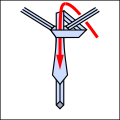
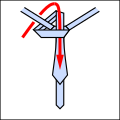
Podstawową ideą jest to, że węzły krawata można opisać jako sekwencję pięciu różnych możliwych ruchów, chociaż nie wszystkie ruchy mogą następować po sobie. Są one podsumowane w następujący sposób. Wszystkie schematy są takie, jak wyglądałby krawat, gdybyś go założył i spojrzał w lustro.

• L : lewy; C : środek; R : dobrze; te muszą zmieniać każdy ruch.
• i : do diagramu; o : poza diagramem; te muszą występować naprzemiennie.
• T : przez właśnie wykonaną pętlę.

Za pomocą tego skrótu można zwięźle wyrazić tradycyjne i nowe węzły, jak poniżej. Zwróć uwagę, że każdy węzeł, który zaczyna się ruchem o , musi zaczynać się od krawata wywróconego na lewą stronę wokół szyi.

• Przykłady wiązania krawatów.
• 

  Li początek.

• 

  Początek .

• 

  Lo

• 

  Ro

• 

  Li

• 

  Ri

• 

  Koniec Lo Ri Co T.

• 

  Koniec Ro Li Co T.

Węzły

Kryteria wyboru

Spośród 85 węzłów możliwych do zawiązania typowym krawatem Fink i Mao wybrali trzynaście jako „węzły estetyczne” nadające się do użytku. Wyboru dokonali na podstawie trzech kryteriów: kształtu, symetrii i równowagi.

Kształt

W klasyfikacji Finka i Mao każdy z 85 węzłów krawata należy do określonej „klasy”, która jest zdefiniowana przez całkowitą liczbę ruchów i liczbę ruchów centrujących. Na przykład czwórka to węzeł z czterema ruchami i jednym centralnym węzłem, podczas gdy pół-Windsor to węzeł z sześcioma ruchami i dwoma środkowymi ruchami. Węzły z mniejszą liczbą ruchów centrujących, mniej niż jedną trzecią całości, wydają się węższe i bardziej wydłużone, podczas gdy węzły z większą liczbą ruchów centrujących wydają się szersze i bardziej przysadziste. Ze względu na trójkątny charakter węzłów krawata, liczba ruchów centrujących musi być koniecznie mniejsza niż połowa całkowitej liczby ruchów.

Istnieje w sumie 16 klas, od trzech ruchów z jednym centrum do dziewięciu ruchów z czterema centrami, ale tylko klasy, w których stosunek ruchów centrujących do wszystkich ruchów wynosi 1: 6 lub więcej, zawierają węzeł estetyczny, eliminujący trzy klasy ( dziesięć węzłów) dla pozostałych 13 klas, z 75 węzłami. (W naturze papier, dolna granica została umieszczona na bardziej restrykcyjnym 1: 4, eliminując klasy węzłów zawierające Kelvin, Victoria i Grantchester; prawdopodobnie zostało to poprawione specjalnie w celu uwzględnienia Wiktorii / Księcia Alberta, który ma dość obszerną dokumentację historyczną). Następnie wybrano najbardziej reprezentatywny węzeł w każdej pozostałej klasie na podstawie symetrii i równowagi.

Symetria

Symetria w przypadku węzłów krawata może odnosić się do dwóch możliwych cech: symetrii wizualnej (stopień, w jakim węzeł wydaje się mieć identyczny kształt po lewej i prawej stronie) oraz symetrii matematycznej (liczba ruchów w lewo i w prawo jest zbliżona do siebie) możliwie równe). Fink i Mao odnoszą się do tego drugiego, chociaż niektóre sęki, które są nieco asymetryczne (takie jak Nicky i Windsor), wydają się symetryczne dla oka. Tylko węzły z równą liczbą całkowitych ruchów w lewo i w prawo mogą być matematycznie symetryczne, podczas gdy pozostałe węzły estetyczne będą miały koniecznie jeden większy ruch w lewo lub w prawo.

Balansować

Fink i Mao opisują równowagę jako „stopień, w jakim ruchy są dobrze wymieszane”, powołując się na mocniejszy węzeł, który trudniej się rozluźnia, jako swoją główną zaletę. Jest obliczany za pomocą określonego wzoru, ale laik może to najlepiej zrozumieć jako stopień, w jakim ruchy L, R i C są równomiernie rozłożone w sekwencji wiązania oraz stopień, w jakim wzór LR lub RL jest kontynuowany nieprzerwanie po niekońcowe ruchy centrujące (co wymaga zmiany kierunku nawijania z przeciwnego do ruchu wskazówek zegara na zgodny z ruchem wskazówek zegara lub odwrotnie). Każdy z estetycznych węzłów wykazuje te cechy.

Wiele węzłów ma praktycznie identyczne warianty, które różnią się transpozycją par L i R. Na przykład wariantem Half-Windsoru, Li Ro Ci Lo Ri Co T (węzeł 7), jest węzeł Li Ro Ci Ro Li Co T (węzeł 8), czasami nazywany współ-pół-Windsorem. Odniesienia do Half-Windsor w literaturze czasami odnoszą się do jednego, czasami do drugiego. Dla celów książki, gdy węzeł ma co najmniej jeden wariant (tj. gdy dwa lub więcej węzłów o największym stopniu symetrii dla swojej klasy ma tę samą podstawową strukturę oprócz jednej lub więcej transponowanych par LR), najbardziej wyważona wersja ma standardowe oznaczenie, podczas gdy inne są oznaczone jako warianty, niezależnie od takich cech, jak samoodblokowanie (cofanie się po wyciągnięciu wąskiego końca). W związku z tym bardziej zrównoważony z dwóch węzłów „pół-Windsor” otrzymuje niższą numerację i nazwę „Half-Windsor”, mimo że nieco mniej zrównoważony wariant „współ-pół-Windsor” jest równie znany jako „pół-Windsor”. Windsor” w literaturze męskiej i ma tę zaletę, że sam się uwalnia, a najczęstszym sposobem wiązania węzła Windsor jest nazywany przez Finka i Mao „co-Windsor 3”. Nie ma to jednak na celu zaznaczenia preferencji estetycznej dla jednego wariantu nad innymi; jak zauważają autorzy w swoich artykułach w czasopismach: „Nie próbujemy odróżnić tych węzłów od ich odpowiedników; to pozostawiamy do uznania czytelnika”.

Trzy estetyczne węzły (St Andrew, Cavendish i Grantchester) mają takie same wartości symetrii i równowagi, jak co najmniej jeden inny węzeł w swojej klasie; w tym przypadku wydaje się, że zostały wybrane na podstawie tego, jak równomiernie rozprowadzają niezrównoważone części w całym węźle. Można to łatwo zauważyć, gdy patrzy się na te węzły jako kombinację dwóch mniejszych węzłów, ponieważ wartości równowagi każdego składnika sumują się do wartości równowagi końcowego węzła. W niezrównoważonych węzłach, w których wartość równowagi jest nieparzysta, jest ona dzielona w taki sposób, że bardziej niezrównoważona część dwóch znajduje się na początku węzła. Ma to prawdopodobnie na celu pomóc najbardziej zewnętrznej części węzła zachować swój kształt i pozostać napiętym.

13 węzłów estetycznych

Trzynaście węzłów estetycznych opisanych w książce, uporządkowanych według wielkości, jest następujących. Sekwencje końcowe (ostatnie trzy ruchy, które kończą się zawiązaniem węzła) są pogrubione. Węzły są czasami oznaczane wyłącznie przez ich liczbę (np. FM2 dla czwórki, gdzie FM oznacza Fink-Mao). Węzeł jest samorozwiązujący się, jeśli po wyciągnięciu cienkiego końca przez węzeł nie pozostaje żaden węzeł; ponieważ wszystkie węzły zaczynają się po lewej stronie, węzeł jest samorozwiązujący się, jeśli końcową sekwencją jest Ro Li Co ; nie jest samouwalniający się, jeśli sekwencją końcową jest Lo Ri Co . Symetria i samorozpuszczalność są w rozkładzie komplementarnym dla węzłów o największym stopniu równowagi w swojej klasie.

Numer	Sekwencja	Nazwa	Samouwalniający się	Symetryczny
1.	Lo Ri Co T	Mały węzeł	NIE	Tak
2.	Li Ro Li Co T	Cztery w rękę	Tak	NIE
3.	Lo Ri Lo Ri Co T	kelwin	NIE	Tak
4.	Lo Ci Ro Li Co T	Nicky (samozwalniający się Pratt)	Tak	NIE
6.	Li Ro Li Ro Li Co T	Wiktoria	Tak	NIE
7.	Li Ro Ci Lo Ri Co T	Pół-Windsor	NIE	Tak
12.	Lo Ri Lo Ci Ro Li Co T	Św Andrzeju	Tak	NIE
18.	Lo Ci Ro Ci Lo Ri Co T	Plattsburgh	NIE	Tak
23.	Li Ro Li Co Ri Lo Ri Co T	Cavendisha	NIE	Tak
31.	Li Co Ri Lo Ci Ro Li Co T	Windsoru	Tak	NIE
44.	Lo Ri Lo Ri Co Li Ro Li Co T	Grantchester	Tak	NIE
54.	Lo Ri Co Li Ro Ci Lo Ri Co T	Hanower	NIE	Tak
78.	Lo Ci Ro Ci Lo Ci Ro Li Co T	Balthusa	Tak	NIE

Trzy popularne warianty węzłów są następujące. Są one uwzględnione ze względu na ich powszechność (wariant Pratt, Half-Windsor) lub samouwalnianie się, gdy ich bardziej „estetyczne” odpowiedniki nie są (wariant Half-Windsor, wariant Hanover). Warianty Half-Windsor i Hanover mają tę zaletę, że są zarówno symetryczne, jak i samozwalniające się, ale są mniej zrównoważone niż ich odpowiedniki powyżej:

Numer	Sekwencja	Nazwa	Samouwalniający się	Symetryczny
5.	Lo Ci Lo Ri Co T	Pratta	NIE	NIE
8.	Li Ro Ci Ro Li Co T	Wariant pół-Windsorski	Tak	Tak
55.	Lo Ri Co Ri Lo Ci Ro Li Co T	wariant Hanower	Tak	Tak

Opinie

Książka została zrecenzowana w Nature , The Daily Telegraph , The Guardian , GQ , Physics World i innych.

Linki zewnętrzne

• Węzły krawatów w Curlie
• Samouczek Jeffa Banksa Jak zawiązać krawat