Algebra planarna
W matematyce algebry planarne 1 po raz pierwszy pojawiły się w pracy Vaughana Jonesa na temat standardowego niezmiennika podczynnika II . Zapewniają również odpowiednie ramy algebraiczne dla wielu niezmienników węzłów (w szczególności wielomianu Jonesa ) i zostały użyte do opisu właściwości homologii Khovanova w odniesieniu do składu splątania . Każda algebra planarna podczynnikowa zapewnia rodzinę unitarnych reprezentacji grup Thompsona . Dowolną grupę skończoną (i uogólnienie kwantowe) można zakodować jako algebrę planarną.
Definicja
Ideą algebry planarnej jest schematyczna aksjomatyzacja standardowego niezmiennika .
Planarny splot
(Zacieniowana) planarna plątanina to dane o skończonej liczbie wejściowych , jednym dysku wyjściowym , nieprzecinających się ciągach dających parzystą liczbę, powiedzmy interwały na dysk i jeden - oznaczony interwał na dysk.
Tutaj znak jest pokazany . Na każdym dysku wejściowym jest on umieszczany pomiędzy dwoma sąsiednimi ciągami wychodzącymi, a na dysku wyjściowym jest umieszczany pomiędzy dwoma sąsiadującymi ciągami przychodzącymi. Splot planarny jest zdefiniowany aż do izotopii .
Kompozycja
Aby skomponować dwa płaskie sploty, włóż dysk wyjściowy jednego do wejścia drugiego, mając tyle samo przedziałów, takie samo cieniowanie oznaczonych przedziałów i tak, aby zaznaczone przedziały się Na koniec usuwamy pokrywające się okręgi. Należy zauważyć, że dwa płaskie sploty mogą mieć zero, jeden lub kilka możliwych składów.
Operada planarna
Operada planarna to zbiór wszystkich splotów planarnych (aż do izomorfizmu) o takich kompozycjach.
Algebra planarna
Algebra planarna jest reprezentacją operady planarnej; dokładniej, jest to rodzina przestrzeni wektorowych zwane , na które działa planarna operada, tj. Dla dowolnej plątaniny (z jednym dyskiem wyjściowym i dyskami wejściowymi z ) istnieje mapa wieloliniowa
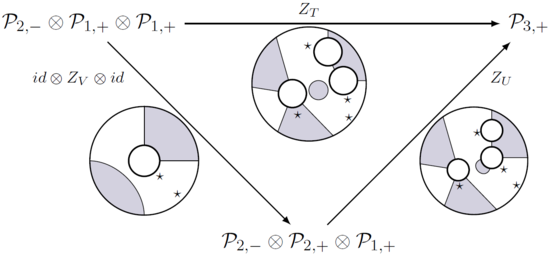
z zgodnie z cieniowaniem przedziałów i tych map (również zwane funkcjami podziału) uwzględniają skład splotu w taki sposób, że wszystkie diagramy jak poniżej są komutowane.
Przykłady
Sploty planarne
Rodzina przestrzeni wektorowych generowanych przez sploty planarne mając na dysku i biały (lub czarny) przyznaje planarną strukturę algebry.
Temperley-Lieb
Płaska algebra Temperleya-Lieba jest generowana przez sploty planarne bez dysku wejściowego; jego przestrzeń -box generowana przez
zamknięty ciąg jest zastępowany mnożeniem
zauważyć, że wymiar to liczba katalońska. } Ta planarna algebra koduje pojęcie algebry Temperleya-Lieba .
Algebra Hopfa
Półprosta i kosemimple algebra Hopfa nad algebraicznie zamkniętym ciałem jest kodowana w planarnej algebrze zdefiniowanej przez generatory i relacje i „odpowiada” (aż do izomorfizmu) połączonej, nieredukowalnej, sferycznej, niezdegenerowanej algebrze planarnej o niezerowym module i głębokości drugiej.
Zauważ, że połączone oznacza (jak do oceny poniżej), nieredukowalne oznacza , kulisty jest zdefiniowany poniżej, a niezdegenerowany oznacza, że ślady (zdefiniowane poniżej) nie są- zdegenerowany.
Algebra planarna podczynnikowa
Definicja
Podczynnik płaska algebra jest płaska -algebra czyli:
- (1) Skończenie-wymiarowe:
- (2) Ocenialne:
- (3) Sferyczny:
- (4) Dodatni: definiuje iloczyn wewnętrzny.
Należy zauważyć, że przy (2) i (3) dowolny zamknięty ciąg (zacieniony lub nie) liczy się dla tej .
Akcja splotu zajmuje się łączeniem poprzez:
z odbiciem { a_ w }
Przykłady i wyniki
Twierdzenie bez ducha Algebra planarna ma ducha (tj. elementu | ) wtedy i tylko wtedy, gdy
Dla jak , niech będzie ideałem zerowym (wygenerowanym przez elementy z ). iloraz jest podczynnikową algebrą planarną, zwaną Jonesa . Dowolna podczynnikowa algebra planarna ze stałą uznaje jako podalgebra planarna
Algebra planarna algebrą planarną wtedy i tylko standardowym ekstremalnego podczynnika indeksu , z i . Skończona głębokość lub nieredukowalny ekstremalny na N ' )
Istnieje planarna algebra podczynnikowa kodująca dowolną skończoną grupę (i bardziej ogólnie, dowolny skończenie wymiarowy -algebra , algebrą Kaca), zdefiniowaną przez generatory i . A (skończenie wymiarowa) algebra Kaca „odpowiada” (aż do izomorfizmu) nieredukowalnej planarnej algebrze podczynnikowej o głębokości drugiej.
Podczynnikowa algebra planarna związana z włączeniem skończonych grup nie zawsze pamięta włączenie (bez rdzenia).
Podczynnik Bischa-Jonesa algebra planarna (czasami nazywana Fuss-katalońskim) zdefiniowany jak dla { ale dopuszczając dwa kolory sznurka z ich własną z jak powyżej. Jest to planarna podalgebra dowolnego podczynnika algebry planarnej z półproduktem, tak że i .
Pierwsza planarna algebra podczynnika skończonej głębokości o podczynnika Haagerupa . Ma indeks }
Podczynnikowe algebry planarne są całkowicie klasyfikowane według indeksu co najwyżej dalej. Klasyfikacja ta została zapoczątkowana przez Uffe Haagerupa . Wykorzystuje (między innymi) listę możliwych głównych grafów wraz z twierdzeniem o osadzaniu i algorytmem meduzy.
Podczynnik algebra planarna pamięta podczynnik (tj. jego standardowy niezmiennik jest kompletny), jeśli jest możliwy. Dopuszczalny jest nadskończony podczynnik o skończonej głębokości.
O przypadku niemożliwym do sklasyfikowania: istnieje wiele nieredukowalnych nadskończonych podczynników indeksu 6, z których wszystkie mają ten sam niezmiennik standardowy.
Transformata Fouriera i biprojekcje
Niech i odpowiadającym mu Załóżmy, że jest nieredukowalne (tj. . Niech pośrednim podczynnikiem. Niech projekcja Jonesa . Zauważ, że } Niech i }
Zauważ, że i .
Niech bijektywna mapa liniowa 2 będzie transformatą Fouriera , zwaną także (zewnętrznej gwiazdy) lub i _ _ _ i }
Należy zauważyć, że słowo koprodukt jest zdrobnieniem od iloczynu splotu . Jest to operacja binarna.
Współprodukt spełnia równość
operatorów współprodukt również można to zobaczyć schematycznie:
Niech przeciwstawną a także . Mapa czterem gwiazdy, więc jest to mapa tożsamości .
W przypadku algebry Kaca przeciwną wartością jest dokładnie antypoda, która dla skończonej grupy odpowiada odwrotności.
Dwuprojekcja to projekcja, w której P } wielokrotność rzutu. Zauważ, że M są biprojekcjami; To może być rozumiane w następujący sposób:
Rzut dwuprojekcją, jeśli jest to projekcja Jonesa displaystyle , jeśli .
Korespondencja Galois : w przypadku algebry Kaca biprojekcje wynoszą 1-1 z lewymi podalgebrami współidealnymi, które dla skończonej grupy odpowiadają podgrupom.
Dla dowolnej nieredukowalnej algebry planarnej podczynnikowej zbiór biprojekcji jest skończoną siecią w postaci jak dla przedziału skończonych grup .
Korzystając z biprojekcji, możemy utworzyć algebry planarne z podczynnikiem pośrednim.
Zasada nieoznaczoności rozciąga się na każdą nieredukowalną podczynnikową algebrę płaską: }
Niech z \ projekcja zakresu nieznormalizowanego śladu (tj. na .
zasada : _ Następnie
Zakładając i zachodzi wtedy i tylko wtedy . Mówiąc bardziej ogólnie, równość zachodzi wtedy i tylko wtedy, gdy bi -przesunięciem .



































![{\displaystyle \delta \in \{2\cos(\pi /n)|n=3,4,5,...\}\cup [2,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0105ecf9dfad64e9ef7d45b51a545b2840b9f76f)






![{\displaystyle [M:N]=\delta ^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d55dae0dce15dae9ad044ba8895fdaff5d20ad73)









![{\displaystyle [K:N]=\delta _{1}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59492aa33355cf94b9b676f6256c24200de16132)
![{\displaystyle [M:K]=\delta _{2}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccf8855a8faf2ba1cde91d3af7db8ea17992a84a)











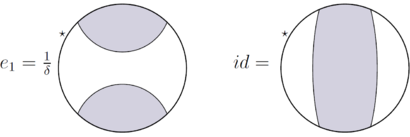
![{\displaystyle tr(e_{1})=\delta ^{-2}=[M:N]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fd63195a24be73213cac05d2a89830dd84f65db)





















![{\displaystyle [e_{1},id]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a75ffda9959472ef1ddde2d3917fc81476c2feda)
![{\displaystyle [H,G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca68a38294795a54c3f9e6dcbf49f347fc7253a7)








