Wygięta geometria molekularna

Wygięta geometria molekularna
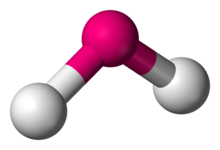Bent-3D-balls.png
Przykłady H2O _ _ , SO2 _
Grupa punktowa C 2v
Numer koordynacyjny 2
Kąt (y) wiązania 90°<θ<120°
μ (biegunowość) >0
Difluorek tlenu , przykład cząsteczki o zakrzywionej geometrii koordynacyjnej.

W chemii cząsteczki o niewspółliniowym układzie dwóch sąsiednich wiązań mają wygiętą geometrię cząsteczkową , znaną również jako kanciasta lub w kształcie litery V. Niektóre atomy, takie jak tlen, prawie zawsze ustawiają swoje dwa (lub więcej) wiązań kowalencyjnych w kierunkach niewspółliniowych ze względu na ich konfigurację elektronową . Woda (H 2 O) jest przykładem wygiętej cząsteczki, a także jej analogów . Kąt wiązania między dwoma atomami wodoru wynosi około 104,45°. Geometria nieliniowa jest powszechnie obserwowana w przypadku innych trójatomowych cząsteczek i jonów zawierających tylko pierwiastki grupy głównej, czego wybitnymi przykładami są dwutlenek azotu (NO 2 ), dichlorek siarki (SCl 2 ) i metylen (CH 2 ).

Ta geometria jest prawie zawsze zgodna z teorią VSEPR , która zwykle wyjaśnia niewspółliniowość atomów obecnością wolnych par . Istnieje kilka wariantów zginania, z których najczęstszym jest AX 2 E 2 , gdzie dwa wiązania kowalencyjne i dwie samotne pary atomu centralnego (A) tworzą kompletną powłokę 8-elektronową . Mają kąty środkowe od 104° do 109,5°, co jest zgodne z uproszczoną teorią, która przewiduje czworościenną symetrię czterech zhybrydyzowanych orbitali sp 3 . Najczęstsze rzeczywiste kąty to 105°, 107° i 109°: różnią się one ze względu na różne właściwości atomów obwodowych (X).

Inne przypadki również doświadczają hybrydyzacji orbitalnej , ale w różnym stopniu. Cząsteczki AX 2 E 1 , takie jak SnCl 2 , mają tylko jedną wolną parę i kąt środkowy około 120° (środek i dwa wierzchołki trójkąta równobocznego ). Mają trzy orbitale sp 2 . Istnieją również zhybrydyzowane przez sd związki metali przejściowych AX 2 bez wolnych par: mają kąt środkowy około 90° i są również klasyfikowane jako zakrzywione. [ Potrzebne źródło ] (Zobacz dalszą dyskusję w teorii VSEPR#Complexes with strong d-contribution ).

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Bent_molecular_geometry&oldid=1106863658 ”