CarMetal

CarMetal
Oryginalni autorzy Erica Hakenholza
Deweloperzy Eric Hakenholz, Patrice Debrabant, Pierre-Marc Mazat, Alain Busser
Pierwsze wydanie 28 października 2006 ( 28.10.2006 )
Wersja stabilna
4.3 / 11 września 2020 r . ; 2 lata temu ( 2020-09-11 )
Magazyn nicEdit this at Wikidata
Napisane w Jawa
Platforma Jawa
Typ Oprogramowanie do interaktywnej geometrii
Licencja Powszechna Licencja Publiczna GNU
Strona internetowa https://carmetal.en.uptodown.com/windows

CaRMetal to interaktywny program do geometrii , który odziedziczył silnik CaR . Oprogramowanie zostało stworzone przez Erica Hakenholza w Javie . CaRMetal jest darmowy, objęty GNU GPL . Zachowuje pewną funkcjonalność CaR, ale używa innego interfejsu graficznego, który rzekomo eliminuje niektóre pośrednie okna dialogowe i zapewnia bezpośredni dostęp do wielu efektów. Konstrukcje są wykonywane przy użyciu głównej palety, która oprócz standardowych narzędzi kompasu i linijki zawiera kilka przydatnych skrótów konstrukcyjnych. Należą do nich dwusieczna prostopadła, okrąg przechodzący przez trzy punkty, łuk kołowy przechodzący przez trzy punkty i przekrój stożkowy przechodzący przez pięć punktów. Interesujące są również loci, funkcje, krzywe parametryczne i wykresy niejawne. Grubość elementu, kolor, etykietę oraz inne atrybuty (w tym tzw. magnetyczne ) można ustawić za pomocą osobnego panelu.

CaRMetal obsługuje również konfigurowalną ograniczoną paletę konstrukcyjną i ma możliwości przypisania, które wykorzystują pozornie unikalną funkcję o nazwie Monkey . CaRMetal posiada język skryptowy ( JavaScript ), który pozwala użytkownikowi budować dość złożone figury, takie jak fraktale . CaRMetal ma kilka lokalizacji, w tym francuski, angielski, hiszpański, niemiecki, włoski, holenderski, portugalski i arabski.

Zainteresowania dydaktyczne

Oczekiwanie

Konstruując linię równoległą , podąża ona za myszką, co ułatwia snucie domysłów , nawet gdy figura jest jeszcze w budowie.

Kiedy wybiera się narzędzie, takie jak równoległość do linii przechodzącej przez punkt lub okrąg, zamierzony obiekt pojawia się w kolorze żółtym i podąża za ruchami myszy. Pozwala to użytkownikowi na domysły jeszcze przed zakończeniem budowy. Ta ciągła interakcja między uczniem a obiektem eksperymentów jest zgodna z nowoczesnymi teoriami dydaktyki iz tego punktu widzenia CaRMetal ma być używany przez uczniów .

Amodalność

Okna pokazujące historię, paletę narzędzi, właściwości wybranego obiektu znajdują się wokół figury, nigdy nad nią. Okna te nie są oknami modalnymi w tym sensie, że nigdy nie zasłaniają konstrukcji. Na przykład, gdy użytkownik chce zmienić kolor wielokąta, natychmiast widzi nowy kolor.

Transformacje

zdefiniowano transformację (na przykład makro ), która przekształca punkty w punkty, transformację tę można również zastosować do krzywych. Po raz kolejny pozwala to uczącemu się na pierwszy rzut oka zobaczyć właściwości transformacji, nawet zanim transformacja została faktycznie zastosowana.

Zadania

przycisk Małpa

Zeszyty ćwiczeń (patrz poniżej) można wyeksportować jako pliki HTML z ograniczoną paletą narzędzi (na przykład pozostawienie tylko narzędzi do przecinania i okręgu pozwala uczniowi na tworzenie konstrukcji tylko z kompasem). Aby utworzyć zadanie, nauczyciel wybiera początkowe obiekty, przedmioty, które uczeń ma stworzyć, i pisze tekst wyjaśniający, co ma zrobić. Od 2010 roku, kiedy uczeń ukończył konstrukcję i chce ją przetestować, testuje przypadkowe warianty (za pomocą narzędzia o nazwie Małpa ) i przypisuje uczniowi notę ​​jakości (właściwie procent dobrych konstrukcji wśród wariantów).

Makra

Makra mogą być zorganizowane w hierarchię folderów, co ułatwia przekształcenie CaRMetal w narzędzie do eksploracji geometrii nieeuklidesowych.

Cechy szczególne

Zeszyty ćwiczeń

Od 2010 roku CaRMetal stosuje system folderów, który pozwala umieścić kilka rysunków w jednym folderze, zwanym „skoroszytem”. Łatwo jest nawigować między arkuszami skoroszytu, powielać arkusz (lub rysunek), łączyć kilka skoroszytów w jeden. CaRMetal pozwala dołączyć do rysunku pliki graficzne i pliki JavaScript. Rozszerzenie pliku figury to zir jak w CaR (nawiasem mówiąc, oba programy są bardzo kompatybilne), a struktura pliku to metaopis figury w języku XML . Ale skoroszyt jest zapisywany jako spakowany folder zawierający wszystkie zir , a także dołączone obrazy ( GIF , JPEG lub PNG ) i plik preferencji .

Wyświetlacz numeryczny

Przykład macierzy , którą można zmieniać w czasie rzeczywistym za pomocą końców wektorów i wyświetlać w LaTeX-u .

Możliwe jest przekonwertowanie dowolnej miary liczbowej figury na tekst, w celach wyświetlania. Na przykład, jeśli segment o nazwie „s1” ma długość 4,5 jednostki, zapis

"Długość segmentu to %s1%"

tworzy ciąg znaków, który jest wyświetlany jako Długość segmentu wynosi 4,5 . Ten ciąg znaków można umieścić na rysunku, ale także ustawić jako alias obiektu (na przykład s1 ) lub nazwę wyrażenia. Oczywiście przesuwanie myszką jednym z końców segmentu powoduje edycję tekstu w czasie rzeczywistym. Nazywa się to tekstem dynamicznym.

CaRMetal używa HotEqn i JLatexMath , które są parserami LaTeX i możliwe jest pisanie formuł LaTeX wewnątrz obiektów tekstowych. Na przykład, jeśli poly1 jest kwadratem, a ktoś chce znaleźć okrąg, którego pole jest takie samo jak pole kwadratu, można zbudować wyrażenie tekstowe w następujący sposób:

„Promień okręgu to $\sqrt{\frac{%poly1%}{\pi}}\simeq %sqrt(poly1/pi)%$”

To może dać tekst taki jak ten:

Siła tej funkcji polega na tym, że można mieszać dynamiczne teksty z formułami LaTeX-a, uzyskując dynamiczny LaTeX (gdy zmienia się rozmiar kwadratu, zmienia się też sposób wyświetlania)!

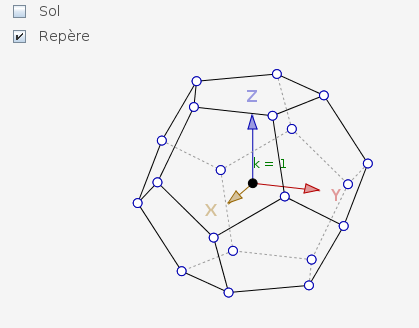
3D

dwunastościan można obracać myszką

CaRMetal pozwala użytkownikowi ustawić pewne właściwości obiektów, takie jak ich kolor czy fakt, że są widoczne lub nie, jako warunkowe . Również każdy obiekt może mieć numer warstwy. Ważnym zastosowaniem tych funkcji był 2,5D CaRMetal, emulujący geometrię 3D. Od wersji 4.0 CaRMetal posiada prawdziwy tryb 3D, który zawiera czworościan foremny , sześcian , romb i dwunastościan foremny . Możliwe jest również powiązanie punktu z wnętrzem (3D) okręgu lub wielokąta. Cecha ta, odziedziczona po CaR , jest oparta na współrzędnych barycentrycznych . Od wersji 4.1 CaRMetal zezwala na niektóre grafiki żółwi (zaprogramowane w JavaScript) w 2D lub 3D.

Magnetyzm

Punkt można uczynić magnetycznym za pomocą odległości i listy obiektów, do których jest przyciągany, gdy punkt znajduje się wystarczająco blisko jednego lub kilku z tych obiektów (wystarczająco blisko oznacza, że ​​odległość między nimi jest mniejsza niż minimalna odległość, która jest właściwością punkt i jest mierzony w jednostkach pikseli ). Na przykład, gdy punkt jest przyciągany do skończonego zestawu punktów, które same są stałe, może badać skończoną geometrię .

Sieć

Od 2013 roku istnieje możliwość uruchomienia jednej postaci CaRMetal jako serwera (zwykle nauczyciela) oraz kilku jako klientów. Dlatego jest to możliwe

  • wysłać swoją figurkę na serwer
  • dla serwera, aby wysłać poprawną figurę do ucznia, który ją zgubił lub nie może jej stworzyć w wymaganym czasie
  • zbierać dane, geometryczne lub nie, w obrębie jednej figury (serwera)
  • manipulować tą samą figurą w tym samym czasie, dla kilku osób, które dzielą się swoją pracą
  • do wysyłania i odbierania programów JavaScript (patrz poniżej)
  • rozmawiać w ramach wspólnej postaci...

JavaScript wewnątrz CaRMetal

Narzędzie skryptowe łączy w sobie algorytmikę i geometrię . Takie narzędzia skryptowe istnieją również w DrGeo , Kig i Cinderella (oprogramowanie) . Aby uruchomić skrypt, należy kliknąć ikonę przedstawiającą sygnalizację świetlną . Skrypt można dołączyć do jednego lub kilku punktów, tak aby każdy ruch jednego z tych punktów uruchamiał skrypt. Pozwala to na pewną kinematykę odwrotną, podobnie jak w przypadku GeoLicia.

Zmienne

Aby stworzyć obiekt geometryczny w JavaScript wystarczy kliknąć na ikonę przedstawiającą obiekt. W edytorze pojawia się instrukcja JavaScript z predefiniowanymi parametrami. Użytkownik musi wtedy tylko je edytować i nie musi używać mnemotechniki . Ale kiedy tworzony jest obiekt geometryczny, zmienna, która wywołała procedurę, jest tak naprawdę ciągiem znaków zawierającym nazwę obiektu.

Na przykład,

 za  =  Punkt  (  2  ,  3  );

tworzy punkt, zwykle nazywany P1 , a zmienna a zawiera napis „P1”. Pozwala to na odniesienie się do punktu po nazwie. Współrzędne punktu są inicjowane, ale punkt nadal można przesuwać za pomocą myszy. Możliwe jest również utworzenie punktu w programowaniu proceduralnym za pomocą 

 Punkt  (  "A"  ,  2  ,  3  );

W tym przypadku nazwa punktu to „A” (chyba, że ​​istnieje już obiekt o nazwie „A”) i żadna zmienna nie jest ustawiona na nazwę „A”.

Wejście wyjście

Aby wyprowadzić zmienną, istnieją cztery sposoby:

  1. Utwórz wyrażenie wewnątrz figury (lub wyświetl średnią graficzną, taką jak histogram);
  2. Drukuj , który otwiera nowe okno i drukuje w nim zawartość zmiennej;
  3. Println , który również trafia do linii;
  4. Alert , który otwiera okno alertu, które zamyka się, gdy tylko użytkownik kliknie OK .

Aby wprowadzić zmienną, jest

  1. Wejście (zakładasz!), które otwiera okno wprowadzania (z tekstem) i czeka na kliknięcie OK
  2. InteractiveInput , która pozwala użytkownikowi wybrać obiekt na rysunku

Ten paradygmat traktuje zmienne programu niekoniecznie jako zmienne liczbowe lub łańcuchowe, ale może również działać na obiektach graficznych. Jest to wspólna cecha Kiga (ale w tym przypadku językiem jest Python (język) ) i DrGeo (w tym przypadku Scheme (język) ).

Smyczki

Możliwe jest również ustawienie współrzędnych punktu jako ciągów znaków napisanych w języku CaRMetal. Na przykład, aby mieć punkt B , który następuje po A, z wyjątkiem tego, że współrzędne B są liczbami całkowitymi (aby modelować liczbę całkowitą gaussowską ), można napisać 


 a  =  Punkt  (  "2,72"  ,  "3,14"  );  b  =  Punkt  (  "round(x_a)"  ,  "round(y_a)"  );

Pętle

Na przykład trójkąt Sierpińskiego można zbudować jako iterowany system funkcji za pomocą tego skryptu rekurencyjnego, który jest raczej krótki ze względu na już dostępne instrukcje graficzne, takie jak MidPoint : 



0


0
	          
	
		   
		
		   
		
		   
		
	
	
	
 a  =  Punkt  (  -  4  ,  -  2  );  b  =  Punkt  (  4  ,  -  2  );  c  =  punkt  (  ,  4  );  m  =  Punkt  (  Matematyka  .  losowo  (),  Matematyka  .  losowo  ());  UstawUkryj  (  m  ,  prawda  );  for  (  n  =  ;  n  <  2000  ;  n  ++  ) {  kostka  =  Matematyka  .  ceil  (  Math  .  random  ()  *  3  );  //Trzyścienne kości!  przełącznik  (  kostka  ) {  przypadek  1  :  {  p  =  punkt środkowy  (  a  ,  m  );  przerwa  ;  }  przypadek  2  :  {  p  =  punkt środkowy  (  b  ,  m  );  przerwa  ;  }  przypadek  3  :  {  p  =  punkt środkowy  (  c  ,  m  );  przerwa  ;  }  }  SetPointType  (  p  ,  "punkt"  );  m  =  p  ;  }

Po zbudowaniu chmury punktów (i nawet podczas działania skryptu!) można przesuwać A , B i C za pomocą myszy (lub automatycznie za pomocą Małpy ): Trójkąt jest dynamiczny !

Obiekty JavaScript

CaRMetal może również używać obiektów JavaScript, takich jak

  1. tablice przydatne do tworzenia statystyk figur geometrycznych;
  2. obiekt daty, przydatny do mierzenia czasu;
  3. String i RegExp , które ułatwiają implementację L-systemów ;
  4. Ogólne obiekty JavaScript mogą być używane do tworzenia nowych obiektów geometrycznych, takich jak liczby zespolone , macierze itp. To programowanie obiektowe działa bardzo podobnie do skryptów Kig w Pythonie , ale wydaje się, że na dzień dzisiejszy nikt nie opublikował niczego, co by to wykorzystywało.

Zobacz też

  • Vers des spécifications formelles: Fondements Mathématiques et Informatiques pour la Géométrie Dynamique, Bernard Genevès (PhD) PDF
  • Busser Alain. TP sous JavaScript avec CarMetal. Bulletin de l'APMEP, 487 (2010), s. 191-199.
  • Busser Alain. Un an d'algorithmique avec CarMetal en Seconde. MathémaTICE, 21 (2010) (artykuł online: [1] )
  • Marcin Yves. Algorithmique et integration des outils. Reperes IREM, 79 (2010), s. 5-22.
  • Marcin Yves. Géométrie repérée dynamique: une autre voie vers l'algébrisation? MathémaTICE, 20 (2010) (dostępny online: [2] )
  • Marcin Yves. Quand la géométrie dynamique rencontre la programmation. In Actes du colloque « Les mathématiciens et l'enseignement de leur distribution en France » ( CIRM , Marsylia/Luminy, 15-19 marca 2010 r.) (wideo online: [3] )
  • Marcin Yves. CaRMetal, une géométrie dynamique wzbogacanie. Wyrażenia, 35 (2010), s. 165-272PDF _

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=CaRMetal&oldid=1132267636 ”