Diagram wpływu

Nie mylić z binarnym diagramem decyzyjnym .

Diagram wpływu ( ID ) (zwany także diagramem istotności , diagramem decyzyjnym lub siecią decyzyjną ) jest zwartą graficzną i matematyczną reprezentacją sytuacji decyzyjnej. Jest to uogólnienie sieci bayesowskiej , w której można modelować i rozwiązywać nie tylko problemy wnioskowania probabilistycznego , ale także problemy decyzyjne (zgodnie z kryterium maksymalnej oczekiwanej użyteczności ).

Identyfikator został po raz pierwszy opracowany w połowie lat 70. przez analityków decyzyjnych z intuicyjną semantyką, która jest łatwa do zrozumienia. Jest obecnie szeroko stosowany i staje się alternatywą dla drzewa decyzyjnego , które zazwyczaj cierpi z powodu wykładniczego wzrostu liczby gałęzi z każdą modelowaną zmienną. ID ma bezpośrednie zastosowanie w analizie decyzji zespołowych, ponieważ umożliwia jawne modelowanie i rozwiązanie niepełnego udostępniania informacji między członkami zespołu. Rozszerzenia ID znajdują również zastosowanie w teorii gier jako alternatywna reprezentacja drzewa gry .

Semantyka

ID to skierowany acykliczny graf z trzema typami (plus jeden podtyp) węzłów i trzema typami łuków (lub strzałek) między węzłami.

węzły:

  • Węzeł decyzyjny (odpowiadający każdej decyzji do podjęcia) rysowany jest jako prostokąt.
  • Węzeł niepewności (odpowiadający każdej modelowanej niepewności) jest rysowany jako owal.
  • Węzeł deterministyczny (odpowiadający szczególnemu rodzajowi niepewności, którego wynik jest deterministycznie znany, gdy znany jest również wynik niektórych innych niepewności) jest rysowany jako podwójny owal.

łuki:

  • Łuki funkcyjne (zakończone węzłem wartości) wskazują, że jednym ze składowych addytywnie separowalnej funkcji użyteczności jest funkcja wszystkich węzłów na ich końcach.
  • Łuki warunkowe (kończące się w węźle niepewności) wskazują, że niepewność na ich głowach jest probabilistycznie uwarunkowana na wszystkich węzłach na ich ogonach.
  • Łuki warunkowe (kończące się węzłem deterministycznym) wskazują, że niepewność na ich głowach jest deterministycznie uwarunkowana na wszystkich węzłach na ich ogonach.
  • Łuki informacyjne (kończące się węzłem decyzyjnym) wskazują, że decyzja na ich czele jest podejmowana przy znanym wcześniej wyniku wszystkich węzłów na ich ogonach.

Biorąc pod uwagę odpowiednio skonstruowany identyfikator:

  • Węzły decyzyjne i przychodzące łuki informacyjne wspólnie określają alternatywy (co można zrobić, gdy wynik pewnych decyzji i/lub niepewności są znane z góry)
  • Węzły niepewności / deterministyczne i przychodzące łuki warunkowe wspólnie modelują informacje ( co jest znane i ich relacje probabilistyczne / deterministyczne)
  • Węzły wartości i przychodzące łuki funkcjonalne wspólnie określają ilościowo preferencje (jak rzeczy są preferowane względem siebie).

Alternatywa, informacja i preferencja są nazywane podstawą decyzji w analizie decyzyjnej, reprezentują trzy wymagane składniki każdej ważnej sytuacji decyzyjnej.

Formalnie semantyka diagramu wpływów opiera się na sekwencyjnej konstrukcji węzłów i łuków, co implikuje określenie wszystkich zależności warunkowych na diagramie. Specyfikacja jest zdefiniowana przez separacji sieci bayesowskiej. Zgodnie z tą semantyką, każdy węzeł jest probabilistycznie niezależny od swoich węzłów niebędących następcami, biorąc pod uwagę wynik jego węzłów bezpośrednio poprzedzających. Podobnie brakujący łuk między węzłem niebędącym wartością węzłem niebędącym wartością że istnieje zestaw węzłów niebędących wartościami np. rodziców , który sprawia, że { jest niezależny od węzły w .

Przykład

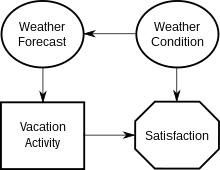
Prosty diagram wpływu na podejmowanie decyzji o aktywności wakacyjnej

Rozważmy prosty diagram wpływu przedstawiający sytuację, w której osoba podejmująca decyzje planuje wakacje.

  • Istnieje 1 węzeł decyzyjny ( aktywność wakacyjna ), 2 węzły niepewności ( warunki pogodowe, prognoza pogody ) i 1 węzeł wartości ( zadowolenie ).
  • Istnieją 2 łuki funkcjonalne (kończące się satysfakcją ), 1 łuk warunkowy (kończący się prognozą pogody ) i 1 łuk informacyjny (kończący się czynnością wakacyjną ).
  • Łuki funkcjonalne zakończone satysfakcją wskazują, że satysfakcja jest funkcją użyteczności warunków pogodowych i aktywności na wakacjach . Innymi słowy, ich satysfakcję można określić ilościowo, jeśli wiedzą, jaka jest pogoda i jaki jest ich wybór aktywności. (Zauważ, że nie cenią prognozy pogody )
  • Warunkowy łuk kończący się na prognozie pogody wskazuje na ich przekonanie, że prognoza pogody i warunki pogodowe mogą być zależne.
  • Łuk informacyjny kończący się słowem Aktywność na wakacjach wskazuje, że podczas dokonywania wyboru będą znali tylko prognozę pogody , a nie warunki pogodowe . Innymi słowy, rzeczywista pogoda będzie znana po dokonaniu wyboru, a na tym etapie mogą liczyć tylko na prognozę.
  • Wynika to również semantycznie, na przykład, że aktywność wakacyjna jest niezależna od (nieistotna) warunków pogodowych , gdy znana jest prognoza pogody .

Możliwość zastosowania do wartości informacji

Powyższy przykład podkreśla moc diagramu wpływu w przedstawianiu niezwykle ważnego pojęcia w analizie decyzji, jakim jest wartość informacji . Rozważ następujące trzy scenariusze;

  • Scenariusz 1: Osoba podejmująca decyzje może podjąć decyzję dotyczącą aktywności na wakacjach , wiedząc, jakie będą warunki pogodowe . Odpowiada to dodaniu dodatkowego łuku informacyjnego od Warunków pogodowych do Aktywności wakacyjnej na powyższym diagramie wpływu.
  • Scenariusz 2: Oryginalny diagram wpływu, jak pokazano powyżej.
  • Scenariusz 3: Decydent podejmuje decyzję, nawet nie znając prognozy pogody . Odpowiada to usunięciu łuku informacyjnego z prognozy pogody do aktywności wakacyjnej na powyższym diagramie wpływu.

Scenariusz 1 jest najlepszym możliwym scenariuszem dla tej sytuacji decyzyjnej, ponieważ nie ma już niepewności co do tego, na czym im zależy ( Warunki pogodowe ) przy podejmowaniu decyzji. Scenariusz 3 jest jednak najgorszym możliwym scenariuszem dla tej sytuacji decyzyjnej, ponieważ muszą podjąć decyzję bez żadnej wskazówki ( Prognoza pogody ), na czym im zależy ( Warunki pogodowe ).

Decydent jest zwykle w lepszej sytuacji (zdecydowanie nie w gorszej sytuacji średnio), aby przejść ze scenariusza 3 do scenariusza 2 poprzez pozyskanie nowych informacji. Najwyżej, jaką powinni zapłacić za takie posunięcie, nazywa się wartość informacji o Prognozie Pogody , która zasadniczo jest wartością niedoskonałych informacji o Warunkach Pogody .

Podobnie dla decydenta najlepiej jest przejść ze scenariusza 3 do scenariusza 1. Najwyższą cenę, jaką powinien zapłacić za takie posunięcie, nazywa się wartością doskonałej informacji o Warunkach Pogodowych .

Możliwość zastosowania tego prostego identyfikatora i wartość koncepcji informacyjnej są ogromne, szczególnie w podejmowaniu decyzji medycznych, kiedy większość decyzji musi być podejmowana przy niedoskonałych informacjach o ich pacjentach, chorobach itp.

Pojęcia pokrewne

Diagramy wpływu są hierarchiczne i można je zdefiniować pod względem ich struktury lub bardziej szczegółowo pod względem funkcjonalnej i liczbowej relacji między elementami diagramu. Identyfikator, który jest spójnie zdefiniowany na wszystkich poziomach — struktury, funkcji i liczby — jest dobrze zdefiniowaną reprezentacją matematyczną i jest określany jako dobrze sformułowany diagram wpływu (WFID). WFID można oceniać za pomocą operacji odwracania i usuwania w celu uzyskania odpowiedzi na dużą klasę pytań probabilistycznych, wnioskowania i decyzji. Nowsze techniki zostały opracowane przez naukowców zajmujących się sztuczną inteligencją Wnioskowanie o sieci bayesowskiej ( propagacja przekonań ).

Diagram wpływu zawierający tylko węzły niepewności (tj. sieć bayesowska) jest również nazywany diagramem istotności . Łuk łączący węzeł A z B oznacza nie tylko, że „ A odnosi się do B ”, ale także, że „ B odnosi się do A ” (tj. istotność jest relacją symetryczną ).

Zobacz też

Bibliografia

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Influence_diagram&oldid=1099923222 ”