Dobrze pokryty wykres

Dobrze pokryty wykres, wykres przecięcia dziewięciu przekątnych sześciokąta . Trzy czerwone wierzchołki tworzą jeden z 14 równych maksymalnych niezależnych zestawów, a sześć niebieskich wierzchołków tworzy uzupełniające minimalne pokrycie wierzchołków.

W teorii grafów graf dobrze pokryty to graf nieskierowany , w którym każde minimalne pokrycie wierzchołków ma taki sam rozmiar jak każde inne minimalne pokrycie wierzchołków. Równoważnie są to grafy, w których wszystkie maksymalne zbiory niezależne mają równe rozmiary. Dobrze pokryte wykresy zostały zdefiniowane i po raz pierwszy zbadane przez Michaela D. Plummera w 1970 roku.

Dobrze pokryte grafy obejmują wszystkie pełne grafy , zrównoważone pełne grafy dwudzielne oraz grafy wieży , których wierzchołki reprezentują kwadraty szachownicy, a krawędzie reprezentują ruchy wieży szachowej. Znane charakterystyki dobrze pokrytych grafów sześciennych , dobrze pokrytych grafów bez pazurów i dobrze pokrytych grafów o dużym obwodzie pozwalają na rozpoznanie tych grafów w czasie wielomianowym , ale sprawdzenie, czy inne rodzaje grafów są dobrze pokryte, jest coNP - kompletny problem

Definicje

Pokrycie wierzchołków w grafie to zbiór wierzchołków, które stykają się z każdą krawędzią grafu. Pokrycie wierzchołków jest minimalne lub zbędne, jeśli usunięcie z niego jakiegokolwiek wierzchołka zniszczyłoby właściwość pokrycia. Jest to minimum, jeśli nie ma innego pokrycia wierzchołków z mniejszą liczbą wierzchołków. Dobrze pokryty graf to taki, w którym każde minimalne pokrycie jest również minimalne. W oryginalnym artykule definiującym dobrze pokryte grafy Plummer pisze, że jest to „oczywiście równoważne” właściwości, że każde dwa minimalne pokrycia mają taką samą liczbę wierzchołków jak inne.

Zbiór niezależny w grafie to zbiór wierzchołków, z których żadne dwa nie sąsiadują ze sobą. Jeśli C jest pokryciem wierzchołków grafu G , dopełnienie C musi być zbiorem niezależnym i odwrotnie . C jest minimalnym pokryciem wierzchołków wtedy i tylko wtedy, gdy jego uzupełnienie I jest maksymalnym niezależnym zbiorem, a C jest minimalnym pokryciem wierzchołków wtedy i tylko wtedy, gdy jego dopełnienie jest maksymalnym niezależnym zbiorem. Dlatego graf dobrze pokryty jest równoważnie grafem, w którym każdy maksymalny zbiór niezależny ma ten sam rozmiar, lub grafem, w którym każdy maksymalny zbiór niezależny jest maksymalny.

W oryginalnym artykule definiującym grafy dobrze pokryte definicje te były ograniczone do grafów połączonych , chociaż mają one znaczenie również dla grafów rozłączonych. Niektórzy późniejsi autorzy zastąpili wymóg łączności słabszym wymaganiem, że dobrze pokryty graf nie może mieć żadnych izolowanych wierzchołków. Zarówno dla spójnych dobrze pokrytych grafów, jak i dobrze pokrytych grafów bez izolowanych wierzchołków, nie może być żadnych istotnych wierzchołków , wierzchołków, które należą do każdego minimalnego pokrycia wierzchołków. Dodatkowo każdy dobrze pokryty graf jest grafem krytycznym dla pokrycia wierzchołków w tym sensie, że dla każdego wierzchołka v , usunięcie v z grafu daje graf z mniejszym minimalnym pokryciem wierzchołków.

Kompleks niezależności grafu G jest kompleksem symplicjalnym mającym simplex dla każdego niezależnego zbioru w G . Mówi się, że kompleks uproszczony jest czysty, jeśli wszystkie jego maksymalne uproszczenia mają tę samą liczność, więc dobrze pokryty graf jest równoważnie grafem z czystym kompleksem niezależności.

Przykłady

	A	B	C	D	mi	F	G	H
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	A	B	C	D	mi	F	G	H

Nieatakujące ustawienie ośmiu wież na szachownicy. Jeśli mniej niż osiem wież zostanie umieszczonych na szachownicy w sposób nieatakujący, zawsze można je rozszerzyć do ośmiu wież, które pozostają nieatakujące.

Wykres cyklu o długości cztery lub pięć jest dobrze opisany: w każdym przypadku każdy maksymalny niezależny zbiór ma rozmiar dwa. Cykl o długości siedem i ścieżka o długości trzy są również dobrze omówione. Każdy kompletny graf jest dobrze pokryty: każdy maksymalny niezależny zbiór składa się z jednego wierzchołka. Podobnie, każdy graf skupień (rozłączna suma pełnych grafów) jest dobrze pokryty. Kompletny graf dwudzielny jest dobrze pokryty, jeśli dwie strony jego dwupodziału mają równą liczbę wierzchołków, ponieważ są to tylko dwa maksymalne niezależne zbiory. Graf dopełnienia a Graf bez trójkątów bez izolowanych wierzchołków jest dobrze pokryty: nie ma niezależnych zbiorów większych niż dwa, a każdy pojedynczy wierzchołek można rozszerzyć do niezależnego zbioru dwóch wierzchołków.

Wykres wieży jest dobrze omówiony: jeśli umieści się dowolny zestaw wież na szachownicy tak, aby żadne dwie wieże nie atakowały się nawzajem, zawsze można kontynuować umieszczanie kolejnych nieatakujących wież, aż znajdzie się po jednej w każdym rzędzie i kolumnie szachownicy szachownica. Graf, którego wierzchołkami są przekątne prostego wielokąta i którego krawędzie łączą pary przecinających się przekątnych, jest dobrze pokryty, ponieważ jego maksymalne zbiory niezależne są triangulacjami wielokąta, a wszystkie triangulacje mają taką samą liczbę krawędzi.

Jeśli G jest dowolnym wykresem n -wierzchołków, to iloczyn pierwiastkowy G z grafem jednokrawędziowym (to znaczy grafem H utworzonym przez dodanie n nowych wierzchołków do G , każdy o stopniu pierwszym i każdy przylegający do odrębnego wierzchołka w G ) dobrze kryje. Maksymalny niezależny zbiór w H musi bowiem składać się z dowolnego niezależnego zbioru w G wraz z sąsiadami pierwszego stopnia zbioru komplementarnego, a zatem musi mieć rozmiar n . Mówiąc bardziej ogólnie, biorąc pod uwagę dowolny wykres G wraz z pokryciem kliki (podział p wierzchołków G na kliki), graf G ^p utworzony przez dodanie kolejnego wierzchołka do każdej kliki jest dobrze pokryty; produkt ukorzeniony jest szczególnym przypadkiem tej konstrukcji, gdy p składa się z n jednowierzchołkowych klik. Zatem każdy graf jest indukowanym podgrafem dobrze pokrytego grafu.

Dwudzielność, bardzo dobrze pokryte wykresy i obwód

Favaron (1982) definiuje graf bardzo dobrze pokryty jako graf dobrze pokryty (prawdopodobnie rozłączony, ale bez izolowanych wierzchołków), w którym każdy maksymalny niezależny zbiór (a zatem także każde minimalne pokrycie wierzchołków) zawiera dokładnie połowę wierzchołków. Ta definicja obejmuje ukorzenione iloczyny grafu G i grafu jednokrawędziowego. Obejmuje to również, na przykład, dobrze pokryte dwudzielne grafy badane przez Ravindrę (1977) i Berge (1981) : w grafie dwudzielnym bez izolowanych wierzchołków obie strony dowolnego dwupodziału tworzą maksymalne niezależne zbiory (i minimalne pokrycie wierzchołków), więc jeśli graf jest dobrze pokryty, obie strony muszą mieć tyle samo wierzchołków. W grafie dobrze pokrytym z n wierzchołkami, bez wierzchołków izolowanych, rozmiar maksymalnego zbioru niezależnego wynosi co najwyżej n /2 , więc grafy bardzo dobrze pokryte to grafy dobrze pokryte, w których maksymalny rozmiar zbioru niezależnego jest tak duży, jak to tylko możliwe .

Graf dwudzielny G jest dobrze pokryty wtedy i tylko wtedy, gdy ma doskonale dopasowane M z tą właściwością, że dla każdej krawędzi uv w M indukowany podgraf sąsiadów u i v tworzy kompletny graf dwudzielny . Charakterystykę pod względem dopasowań można rozszerzyć od grafów dwudzielnych do bardzo dobrze pokrytych grafów: graf G jest bardzo dobrze pokryty wtedy i tylko wtedy, gdy ma idealnie dopasowane M o następujących dwóch właściwościach:

1. Żadna krawędź M nie należy do trójkąta w G , i
2. Jeśli krawędź M jest środkową krawędzią ścieżki o trzech krawędziach w G , to dwa końce ścieżki muszą przylegać do siebie.

Co więcej, jeśli G jest bardzo dobrze pokryte, to każde idealne dopasowanie w G spełnia te właściwości.

Drzewa są szczególnym przypadkiem grafów dwudzielnych, a sprawdzanie, czy drzewo jest dobrze pokryte, można potraktować jako znacznie prostszy przypadek specjalny charakteryzowania dobrze pokrytych grafów dwudzielnych: jeśli G jest drzewem z więcej niż dwoma wierzchołkami, to jest dobrze pokryte wtedy i tylko wtedy, gdy każdy nie-liściowy węzeł drzewa sąsiaduje dokładnie z jednym liściem. Ta sama charakterystyka dotyczy grafów, które są lokalnie drzewiaste, w tym sensie, że sąsiedztwa każdego wierzchołka o małej średnicy są acykliczne: jeśli graf ma obwód osiem lub więcej (tak, że dla każdego wierzchołka v podgraf wierzchołków w odległości trzy z w jest acykliczny), to jest dobrze pokryty wtedy i tylko wtedy, gdy każdy wierzchołek stopnia większego od jeden ma dokładnie jednego sąsiada stopnia pierwszego. Ściśle powiązana, ale bardziej złożona charakterystyka dotyczy dobrze pokrytych wykresów o obwodzie pięć lub więcej.

Regularność i planarność

Siedem sześciennych 3-połączonych, dobrze pokrytych grafów

Sześcienny dobrze pokryty graf połączony z 1, utworzony przez zastąpienie każdego węzła sześciowęzłowej ścieżki jednym z trzech fragmentów

Dysfenoid zadarty , jeden z czterech dobrze pokrytych 4-połączonych trójwymiarowych uproszczonych wielościanów.

Sześcienne ( 3-regularne ) dobrze pokryte grafy zostały sklasyfikowane: składają się z siedmiu 3-połączonych przykładów wraz z trzema nieskończonymi rodzinami grafów sześciennych o mniejszej łączności .

Siedem 3-połączonych sześciennych dobrze pokrytych grafów to pełny graf K ₄ , wykresy graniastosłupa trójkątnego i graniastosłupa pięciokątnego , wykres Dürera , wykres użyteczności K _3,3 , wykres ośmiu wierzchołków otrzymany z wykresu użyteczności przez transformatę Y-Δ i 14-wierzchołkowy uogólniony graf Petersena G (7,2) . Spośród tych grafów pierwsze cztery to grafy planarne . Są to jedyne cztery sześcienne grafy wielościenne (wykresy prostych wypukłych wielościanów ), które są dobrze pokryte. Cztery z wykresów (dwa pryzmaty, wykres Dürera i G (7,2) ) to uogólnione wykresy Petersena.

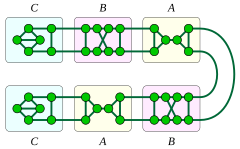
Wszystkie sześcienne dobrze pokryte grafy połączone 1 i 2 są tworzone przez zastąpienie węzłów ścieżki lub cyklu trzema fragmentami grafów, które Plummer (1993) oznacza A , B i C . Fragmenty A lub B mogą zastąpić węzły cyklu lub wewnętrzne węzły ścieżki, podczas gdy fragment C służy do zastąpienia dwóch końcowych węzłów ścieżki. Fragment A zawiera most , więc wynik wykonania tego procesu zamiany na ścieżce i przy użyciu fragmentu A w celu zastąpienia niektórych węzłów ścieżki (i pozostałych dwóch fragmentów dla pozostałych węzłów) jest dobrze pokrytym grafem sześciennym połączonym z 1 wierzchołkiem. Wszystkie dobrze pokryte grafy sześcienne z 1 wierzchołkiem mają tę postać i wszystkie takie grafy są planarne.

Istnieją dwa typy dobrze pokrytych grafów sześciennych połączonych z 2 wierzchołkami. Jedna z tych dwóch rodzin jest tworzona przez zastąpienie węzłów cyklu fragmentami A i B , przy czym co najmniej dwa fragmenty są typu A ; graf tego typu jest planarny wtedy i tylko wtedy, gdy nie zawiera żadnych fragmentów typu B . Druga rodzina jest tworzona przez zastąpienie węzłów ścieżki fragmentami typu B i C ; wszystkie takie grafy są planarne.

Uzupełniając charakterystykę dobrze pokrytych wielościanów prostych w trzech wymiarach, badacze wzięli również pod uwagę dobrze pokryte wielościany proste lub równoważnie dobrze pokryte maksymalne grafy planarne. Każdy maksymalny graf planarny z pięcioma lub więcej wierzchołkami ma spójność wierzchołków 3, 4 lub 5. Nie ma dobrze pokrytych 5-połączonych maksymalnych grafów planarnych, a są tylko cztery 4-połączone, dobrze pokryte maksymalne grafy planarne: wykresy regularny ośmiościan , pięciokątna dwupiramida , zadarty disfenoid i nieregularny wielościan (niewypukły deltaedr ) z 12 wierzchołkami, 30 krawędziami i 20 trójkątnymi ścianami. Jednak istnieje nieskończenie wiele 3-połączonych, dobrze pokrytych maksymalnych grafów planarnych. Na przykład, jeśli 3 wierzchołkach t ma t rozłącznych ścian trójkąta, to ściany te utworzą pokrycie kliki. Dlatego konstrukcja pokrycia kliki, która w przypadku tych grafów polega na podzieleniu każdego z tych t na trzy nowe trójkąty spotykające się w środkowym wierzchołku, tworzy dobrze pokryty maksymalny graf planarny.

Złożoność

Testowanie, czy graf zawiera dwa maksymalne niezależne zbiory o różnych rozmiarach, jest NP-zupełne ; to znaczy, komplementarnie, testowanie, czy wykres jest dobrze pokryty, jest coNP-zupełne. Chociaż łatwo jest znaleźć maksymalne niezależne zbiory w grafach, o których wiadomo, że są dobrze pokryte, jest również NP-trudne dla algorytmu wygenerowanie jako wynik, na wszystkich grafach, albo maksymalnego niezależnego zbioru, albo gwarancji, że dane wejściowe są niezbyt dobrze kryjący.

Natomiast można sprawdzić, czy dany graf G jest bardzo dobrze pokryty w czasie wielomianowym . Aby to zrobić, znajdź podgraf H z G składający się z krawędzi, które spełniają dwie właściwości dopasowanej krawędzi w bardzo dobrze pokrytym grafie, a następnie użyj algorytmu dopasowującego, aby sprawdzić, czy H ma doskonałe dopasowanie. Niektóre problemy, które są NP-zupełne dla dowolnych grafów, takie jak problem znalezienia cyklu Hamiltona , można również rozwiązać w czasie wielomianowym dla bardzo dobrze pokrytych grafów.

Mówi się, że graf jest równoważny , jeśli każde maksymalne dopasowanie jest maksymalne; to znaczy, że jest równoważny, jeśli jego wykres liniowy jest dobrze pokryty. Silniej nazywa się to dopasowaniem losowym , jeśli każde maksymalne dopasowanie jest dopasowaniem doskonałym . Jedynymi połączonymi losowo dopasowanymi grafami są pełne grafy i zrównoważone pełne grafy dwudzielne. Możliwe jest sprawdzenie, czy wykres liniowy lub bardziej ogólnie wykres bez pazurów jest dobrze pokryty w czasie wielomianowym.

Charakterystyki dobrze pokrytych grafów o obwodzie pięć lub więcej oraz dobrze pokrytych grafów, które są 3-regularne, również prowadzą do wydajnych algorytmów czasu wielomianowego do rozpoznawania tych wykresów.

Notatki

•    Berge, Claude (1981), „Niektóre wspólne właściwości grafów regulowanych, grafów krytycznych dla krawędzi i grafów B ”, Teoria grafów i algorytmy (Proc. Sympos., Res. Inst. Electr. Comm., Tohoku Univ., Sendai, 1980) , Notatki z wykładów z informatyki, tom. 108, Berlin: Springer, s. 108–123, doi : 10.1007/3-540-10704-5_10 , ISBN 978-3-540-10704-0 , MR 0622929 .
• Campbell, SR (1987), Niektóre wyniki dotyczące dobrze pokrytych grafów planarnych , Ph.D. praca magisterska, Uniwersytet Vanderbilt, Wydział Matematyki . Cytowane przez Plummera (1993) .
•   Campbell, Republika Południowej Afryki; Ellingham, Minnesota ; Royle, Gordon F. (1993), „Charakterystyka dobrze pokrytych grafów sześciennych”, Journal of Combinatorial Mathematics and Combinatorial Computing , 13 : 193–212, MR 1220613 .
•   Campbell, Stephen R.; Plummer, Michael D. (1988), „Na dobrze pokrytych 3-polytopach”, Ars Combinatoria , 25 (A): 215–242, MR 0942505 .
•   Caro, Yair; Sebő, András ; Tarsi, Michael (1996), „Rozpoznawanie zachłannych struktur”, Journal of Algorithms , 20 (1): 137–156, doi : 10.1006/jagm.1996.0006 , MR 1368720 .
•   Chvátal, Václav ; Slater, Peter J. (1993), „Notatka o dobrze pokrytych wykresach”, Quo vadis, teoria grafów? , Annals of Discrete Mathematics, tom. 55, Amsterdam: Holandia Północna, s. 179–181, MR 1217991 .
• Gotować, Dawid, II; Nagel, Uwe (2010), „Wykresy Cohena-Macaulaya i wektory twarzy kompleksów flag”, SIAM Journal on Discrete Mathematics , 26 : 89–101, arXiv : 1003,4447 , Bibcode : 2010arXiv1003.4447C , doi : 10,1137/100818170 .
•   Dochtermann, Anton; Engström, Alexander (2009), „Algebraiczne właściwości ideałów krawędzi za pomocą topologii kombinatorycznej”, Electronic Journal of Combinatorics , 16 (2): Research Paper 2, doi : 10.37236/68 , MR 2515765 .
•   Favaron, O. (1982), „Bardzo dobrze pokryte wykresy”, Matematyka dyskretna , 42 (2–3): 177–187, doi : 10.1016/0012-365X (82) 90215-1 , MR 0677051 .
•   Finbow, AS; Hartnell, BL (1983), „Gra związana z zakrywaniem gwiazdami”, Ars Combinatoria , 16 (A): 189–198, MR 0737090 .
•   Finbow, A.; Hartnell, B.; Nowakowski, R. (1988), „Wykresy dobrze zdominowane: zbiór dobrze pokrytych”, Ars Combinatoria , 25 (A): 5–10, MR 0942485 .
•   Finbow, A.; Hartnell, B.; Nowakowski, RJ (1993), „Charakterystyka dobrze pokrytych grafów o obwodzie 5 lub większym”, Journal of Combinatorial Theory , Seria B, 57 (1): 44–68, doi : 10.1006 / jctb.1993.1005 , MR 1198396 .
•   Finbow, A.; Hartnell, B.; Nowakowski R.; Plummer, Michael D. (2003), „O dobrze pokrytych triangulacjach. I”, Discrete Applied Mathematics , 132 (1–3): 97–108, doi : 10.1016 / S0166-218X (03) 00393-7 , MR 2024267 .
•   Finbow, Artur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2009), „O dobrze pokrytych triangulacjach. II”, Discrete Applied Mathematics , 157 (13): 2799–2817, doi : 10.1016/j.dam.2009.03.014 , MR 2537505 .
•   Finbow, Artur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), „O dobrze pokrytych triangulacjach. III”, Discrete Applied Mathematics , 158 (8): 894–912, doi : 10.1016/j.dam.2009.08.002 , MR 2602814 .
•   Finbow, Artur S.; Hartnell, Bert L.; Nowakowski, Ryszard J.; Plummer, Michael D. (2016), „Dobrze pokryte triangulacje: część IV”, Discrete Applied Mathematics , 215 : 71–94, doi : 10.1016/j.dam.2016.06.030 , MR 3548980 .
•   Fink, JF; Jacobson, MS; Kinch, LF; Roberts, J. (1985), „Na wykresach o liczbie dominacji w połowie ich rzędu”, Okres. Matematyka węgierski. , 16 (4): 287–293, doi : 10.1007/BF01848079 , MR 0833264 .
•    Greenberg, Peter (1993), „Piecewise SL ₂ Z geometria”, Transactions of the American Mathematical Society , 335 (2): 705–720, doi : 10.2307/2154401 , JSTOR 2154401 , MR 1140914 .
•   Holroyd, Fred; Talbot, John (2005), „Wykresy z właściwością Erdősa-Ko-Rado”, Matematyka dyskretna , 293 (1–3): 165–176, arXiv : math / 0307073 , doi : 10.1016/j.disc.2004.08.028 , MR 2136060 .
•   Lesk, M.; dr med. Plummera; Pulleyblank, WR (1984), „Equi-matchable graphs”, w Bollobás, Béla (red.), Graph Theory and Combinatorics: Proceedings of the Cambridge Combinatorial Conference, in Honor of Paul Erdös , Londyn: Academic Press, s. 239– 254, MR 0777180 .
•   Plummer, Michael D. (1970), „Niektóre pojęcia obejmujące wykresy”, Journal of Combinatorial Theory , 8 : 91–98, doi : 10.1016/S0021-9800 (70) 80011-4 , MR 0289347 .
•   Plummer, Michael D. (1993), „Dobrze pokryte wykresy: ankieta” , Quaestiones Mathematicae , 16 (3): 253–287, doi : 10.1080/16073606.1993.9631737 , MR 1254158 , zarchiwizowane z oryginału w dniu 27 maja, 2012 .
•   Raghavan, Vijay; Spinrad, Jeremy (2003), „Solidne algorytmy dla domen z ograniczeniami”, Journal of Algorithms , 48 (1): 160–172, doi : 10.1016/S0196-6774 (03) 00048-8 , MR 2006100 .
•   Ravindra, G. (1977), „Dobrze pokryte wykresy”, Journal of Combinatorics, Information and System Sciences , 2 (1): 20–21, MR 0469831 .
• Sankaranarayana, Ramesh S. (1994), Dobrze pokryte wykresy: niektóre nowe podklasy i wyniki złożoności (rozprawa doktorska), University of Alberta
•    Sankaranarayana, Ramesh S.; Stewart, Lorna K. (1992), „Wyniki złożoności dla dobrze pokrytych wykresów”, Networks , 22 (3): 247–262, CiteSeerX 10.1.1.47.9278 , doi : 10.1002/net.3230220304 , MR 1161178 .
• Staples, J. (1975), O niektórych podklasach dobrze pokrytych grafów , Ph.D. praca magisterska, Uniwersytet Vanderbilt, Wydział Matematyki . Cytowane przez Plummera (1993) .
•   Sumner, David P. (1979), „Losowo dopasowane wykresy”, Journal of Graph Theory , 3 (2): 183–186, doi : 10.1002/jgt.3190030209 , MR 0530304 .
•   Tankus, Dawid; Tarsi, Michael (1996), „Dobrze pokryte wykresy bez pazurów”, Journal of Combinatorial Theory , Seria B, 66 (2): 293–302, doi : 10.1006/jctb.1996.0022 , MR 1376052 .
•   Tankus, Dawid; Tarsi, Michael (1997), „Struktura dobrze pokrytych grafów i złożoność ich problemów z rozpoznawaniem”, Journal of Combinatorial Theory , Seria B, 69 (2): 230–233, doi : 10.1006 / jctb.1996.1742 , MR 1438624 .