Dowody tożsamości trygonometrycznych

Istnieje kilka równoważnych sposobów definiowania funkcji trygonometrycznych , a dowód tożsamości trygonometrycznych między nimi zależy od wybranej definicji. Najstarsza iw pewnym sensie najbardziej elementarna definicja opiera się na geometrii trójkątów prostokątnych . Dowody podane w tym artykule wykorzystują tę definicję, a zatem mają zastosowanie do nieujemnych kątów nie większych niż kąt prosty . Kąty większe i ujemne , zobacz Funkcje trygonometryczne .

$tym samym inne$ oparte na szeregu Taylora sinusów i cosinusów lub na równaniu różniczkowym, którego są rozwiązaniami

Elementarne tożsamości trygonometryczne

Definicje

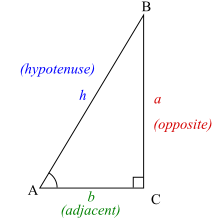
Funkcje trygonometryczne określają relacje między długościami boków i kątami wewnętrznymi trójkąta prostokątnego. Na przykład sinus kąta θ definiuje się jako długość przeciwległego boku podzieloną przez długość przeciwprostokątnej.

Sześć funkcji trygonometrycznych jest zdefiniowanych dla każdej liczby rzeczywistej , z wyjątkiem niektórych z nich dla kątów różniących się od 0 o wielokrotność kąta prostego (90°). Odnosząc się do diagramu po prawej stronie, sześć funkcji trygonometrycznych θ to dla kątów mniejszych niż kąt prosty:

${\ Frac {\ operatorname {naprzeciwko}}$

$_$

${\ Displaystyle \ tan \ theta = {\ Frac {\ operatorname {naprzeciwko}}} {\ operatorname {sąsiedni}}} = {\ Frac {a$

${\ Displaystyle \ łóżeczko \ teta = {\ Frac {\ operatorname {sąsiadujący}}} {\ operatorname {naprzeciwko}}} = {\ Frac {b} {a} }}$

${\ Displaystyle \ sec \ theta = {\ Frac {\ operatorname {przeciwprostokątna}}} {\ operatorname {sąsiedni}}} = {\ Frac {h} {b}}}$

${\ Displaystyle \ csc \ teta = {\ Frac {\ operatorname {przeciwprostokątna}}} {\ operatorname {naprzeciwko}}} = {\ Frac {h} {a}} }$

Tożsamości proporcji

W przypadku kątów mniejszych od kąta prostego następujące tożsamości są bezpośrednimi konsekwencjami powyższych definicji poprzez tożsamość podziału

${\ Displaystyle {\ Frac {a} {b}} = {\ Frac {\ lewo ({\ Frac {a}}} \ prawo)} {\ lewo ({\ Frac {b} {h}} \ Prawidłowy)}}.}$

Zachowują one ważność dla kątów większych niż 90° oraz dla kątów ujemnych.

$\ Displaystyle \ tan \ teta = {\ Frac {\ operatorname {naprzeciwko}}} {\ operatorname {przylegający}}} = {\ Frac {\ lewo ({{ \frac {\mathrm {przeciwprostokątna} }{\mathrm {przeciwprostokątna} }}\right)}{\left({\frac {\mathrm {sąsiedni}}}{\mathrm {przeciwprostokątna} }}\right)}}={ \ frac {\ sin \ theta }{\ cos \ theta }}}$

${\ Displaystyle \ cot \ theta = {\ Frac {\ operatorname {sąsiadujący}}} {\ operatorname {naprzeciwko}}} = {\ Frac {\ lewo ({\ Frac {\ operatorname {sąsiedni}}} {\ operatorname {sąsiadujący} }}\right)}{\left({\frac {\mathrm {naprzeciw} }{\mathrm {przylegający} }}\right)}}={\frac {1}{\tan \theta }}={\ frac$

$sin \theta}}}$

${\ Displaystyle \ sec \ theta = {\ Frac {1} {\ cos \ theta}} = {\ Frac {\ operatorname {przeciwprostokątna}}} {\ operatorname {przylegający}}}}$

${\ Displaystyle \ csc \ teta = {\ Frac {1} {\ sin \ teta}} = {\ Frac {\ operatorname {przeciwprostokątna}$

${\ Displaystyle \ tan \ theta = {\ Frac {\ operatorname {naprzeciwko}}} {\ operatorname {przylegający}}} = {\ Frac {\ lewo ({\ Frac {\ operatorname {naprzeciwko} \ razy \ operatorname {przeciwprostokątna} }{\mathrm {naprzeciwko} \times \mathrm {przylegający} }}\right)}{\left({\frac {\mathrm {przylegający} \times \mathrm {przeciwprostokątna} }{\mathrm {naprzeciwko} \times \ mathrm {przylegający} }}\right)}}={\frac {\left({\frac {\mathrm {przeciwprostokątna} }{\mathrm {przylegający} }}\right)}{\left({\frac {\ mathrm {przeciwprostokątna} }{\mathrm {przeciwprostokątna}}}\right)}}={\frac {\sec \theta }{\csc \theta }}}$

Lub

${\ Displaystyle \ tan \ teta = {\ Frac {\ sin \ teta} {\ cos \ teta}} = {\ Frac {\ lewo ({\ Frac {1} {\ csc \ teta}} \ prawej) }{\left({\frac {1}{\sec \theta}}\right)}}={\frac {\left({\frac {\csc \theta \sec \theta}} {\csc \theta} }\right)}{\left({\frac {\csc \theta \sec \theta}} = {\frac {\sec \theta}} {\csc \theta} }}$

${\ Displaystyle \ łóżeczko \ teta = {\ Frac {\ csc \ teta} {\ sec \ teta}}}$

Tożsamości kąta dopełniającego

Dwa kąty, których suma wynosi π/2 radianów (90 stopni) są komplementarne . Na diagramie kąty w wierzchołkach A i B są komplementarne, więc możemy zamienić aib i zmienić θ na π/2 − θ, otrzymując:

${\ Displaystyle \ sin \ lewo (\ pi / 2- \ teta \ prawej) = \ cos \ teta}$

${\ Displaystyle \ cos \ lewo (\ pi / 2- \ teta \ po prawej) = \ sin \ teta}$

${\ Displaystyle \ tan \ lewo (\ pi / 2- \ theta \ prawej) = \ łóżeczko \ theta} łóżeczko$

$\ Displaystyle \ łóżeczko \ lewo (\ pi / 2- \ theta \ right) = \ tan \ theta }$

${\ Displaystyle \ sec \ lewo (\ pi / 2- \ theta \ right) = \ csc \ theta}$

${\ Displaystyle \ csc \ lewo (\ pi / 2- \ teta \ po prawej) = \ sek \ teta}$

Tożsamości pitagorejskie

Główny artykuł: pitagorejska tożsamość trygonometryczna

Tożsamość 1:

${\ Displaystyle \ sin ^ {2} \ teta + \ sałata ^ {2} \ teta = 1}$

Z tego i tożsamości proporcji wynikają następujące dwa wyniki. Aby uzyskać pierwszą, podziel obie strony ${\ Displaystyle \ sin ^ {2} \ teta + \ cos ^ {2} \ teta = 1}$ przez ${\ styl wyświetlania \cos ^{2}\theta }$ ; po drugie, podziel przez ${\ Displaystyle \ sin ^ {2} \ theta}$ .

${\ Displaystyle \ dębnik ^ {2} \ teta + 1 \ = \ sek ^ {2} \ teta}$

${\ Displaystyle \ sec ^{2}\theta -\tan ^{2}\theta =1}$

podobnie

${\ Displaystyle 1 \ + \ łóżeczko ^ {2} \ teta = \ csc ^ {2} \ teta}$

${\ Displaystyle \ csc ^{2}\theta -\łóżeczko ^{2}\theta =1}$

Tożsamość 2:

Poniżej przedstawiono wszystkie trzy odwrotne funkcje.

${\ Displaystyle \ csc ^ {2} \ teta + \ s ^ {2} \ teta - \ łóżeczko ^ {2} \ teta =2\ +\tan ^{2}\theta }$

Dowód 2:

Patrz schemat trójkąta powyżej. Zauważ, że według twierdzenia Pitagorasa za ${\ Displaystyle a ^ {2} + b ^ {2} = h ^$ }

${\ Displaystyle \ csc ^ {2} \ theta + \ sec ^ {2} \ theta = {\ Frac {h ^ {2}} {a ^ {2}}} + {\ Frac {h ^ {2}} {b^{2}}}={\frac {a^{2}+b^{2}}{a^{2}}}+{\frac {a^{2}+b^{2}} {b^{2}}}=2\ +{\frac {b^{2}}{a^{2}}}+{\frac {a^{2}}{b^{2}}}}$

Zastąpienie odpowiednimi funkcjami -

${\ Displaystyle 2 \ + {\ Frac {b ^ {2}} {a ^ {2}}} + {\ frac {a^{2}}{b^{2}}}=2\ +\tan ^{2}\theta +\cot ^{2}\theta }$

Przegrupowanie daje:

${\ Displaystyle \ csc ^ {2} \ teta + \ s ^ {2} \ teta - \ łóżeczko ^ {2} \ teta =2\ +\tan ^{2}\theta }$

Tożsamości sumy kątów

Zobacz także: Lista tożsamości trygonometrycznych § Tożsamości sumy kątów i różnic

Sinus

Ilustracja formuły sumy.

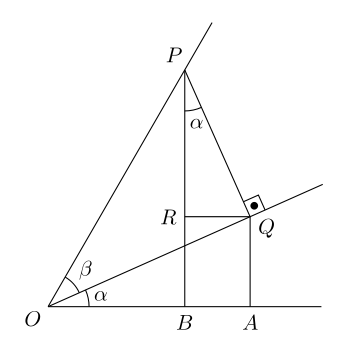
Narysuj linię poziomą ( oś x ); zaznacz początek O. $powyżej$ linię od O pod kątem $linii$ poziomej i drugą linię pod kątem tego; kąt między drugą linią a x wynosi ${\ Displaystyle \ alpha + \ beta}$ .

Umieść P na linii określonej przez ${\ displaystyle \ alpha + \ beta}$ w jednostkowej odległości od początku.

$Niech$ PQ będzie linią prostopadłą do linii OQ wyznaczonej przez kąt poprowadzonej od punktu Q na tej prostej do punktu P. $jest$ kątem prostym.

Niech QA będzie prostopadłą z punktu A na $osi$ x do Q, a PB będzie prostopadłą z punktu B na osi x do P. i OBP są kątami prostymi.

Narysuj R na PB tak, aby QR był równoległy do ​​osi x .

Teraz kąt ${\ Displaystyle RPQ = \ alfa}$ (ponieważ ${\ Displaystyle OQA = {\ Frac {\ pi} {2}}$ - ${\ Displaystyle RQO = \ alfa, RQP = {\ Frac {\ pi} {2}} - \ alfa}$ i wreszcie ${\ Displaystyle RPQ = \ alfa}$ )

${\ Displaystyle RPQ = {\ tfrac {\ pi} {2}} -RQP = {\ tfrac {\ pi} {2}} - ({\ tfrac {\ pi} {2}} -RQO) = RQO = \ alfa}$

${\ Displaystyle OP = 1}$

${\ Displaystyle PQ=\sin \beta }$

${\ Displaystyle OQ = \ sałata \ beta}$

${\ Displaystyle {\ Frac {AQ} {OQ}} = \ sin \ alfa}$ , więc ${\ Displaystyle AQ = \ sin \ alfa \ sałata \ beta}$

${\ Displaystyle {\ Frac {PR} {PQ}} = \ cos \ alfa}$ , więc ${\ Displaystyle PR = \ sałata \ alfa \ grzech \ beta}$

${\ Displaystyle \ sin (\ alfa + \ beta) = PB = RB + PR = AQ + PR = \ sin \ alfa \ cos \ beta + \ cos \ alfa \ sin \ beta}$

Zastępując $używając$$_$ , otrzymujemy również _

${\ Displaystyle \ sin (\ alfa - \ beta) = \ sin \ alfa \ sałata (- \ beta )+\cos \alpha \sin(-\beta )}$

${\ Displaystyle \ sin (\ alfa - \ beta) = \ sin \ alfa \ cos \ beta - \ cos \ alfa \ sin \ beta}$

Cosinus

Korzystając z powyższego rysunku,

${\ Displaystyle OP = 1}$

${\ Displaystyle PQ = \ sin \ beta}$

${\ Displaystyle OQ = \ cos \ beta}$

$_$ _ $_$

${\ Displaystyle {\ Frac {RQ} {PQ}} = \ sin \ alfa}$ , więc ${\ Displaystyle RQ = \ sin \ alfa \ sin \ beta }$

${\ Displaystyle \ cos (\ alfa + \ beta) = OB = OA-BA = OA-RQ = \ cos \ alfa \ cos \ beta \ - \ sin \ alfa \ sin \ beta }$

Zastępując $używając$$_$ , otrzymujemy również _

${\ Displaystyle \ cos (\ alfa - \ beta) = \ sałata \ alfa \ sałata (- \ beta )-\sin \alpha \sin(-\beta ),}$

${\ Displaystyle \ sałata (\ alfa - \ beta) = \ sałata \ alfa \ sałata \ beta + \ grzech \ alfa \ grzech \ beta}$

Ponadto, korzystając ze wzorów na kąty dopełniające,

${\ Displaystyle {\ rozpocząć {wyrównane} \ sałata (\ alfa + \ beta) & = \ sin \ lewo (\ pi /2-(\alpha +\beta )\right)\\&=\sin \left((\pi /2-\alpha )-\beta \right)\\&=\sin \left(\pi /2 -\alpha \right)\cos \beta -\cos \left(\pi /2-\alpha \right)\sin \beta \\&=\cos \alpha \cos \beta -\sin \alpha \sin \ beta \\\koniec {wyrównany}}}$

Styczna i cotangens

Ze wzorów sinus i cosinus otrzymujemy

${\ Displaystyle \ tan (\ alfa + \ beta) = {\ Frac {\ sin (\ alfa + \ beta)}} {\ cos (\ alfa + \ beta)}} = {\ Frac {\ sin \ alfa \ cos \beta +\cos \alpha \sin \beta }{\cos \alpha \cos \beta -\sin \alpha \sin \beta }}}$

Dzieląc zarówno licznik, jak i mianownik przez ${\ Displaystyle \ cos \ alfa \ cos \ beta}$ , otrzymujemy

${\ Displaystyle \ dębnik (\ alfa + \ beta) = {\ Frac {\ tan \ alfa + \ tan \ beta} {1-\tan \alpha \tan \beta }}}$

Odejmując od , używając $tan (- \ beta) = - \ tan$$dębnik$$\$ }

${\ Displaystyle \ tan (\ alfa - \ beta) = {\ Frac {\ tan \ alfa + \ tan (- \ beta)} {1- \ tan \ alfa \ tan (- \ beta)}} = {\ frac {\tan \alpha -\tan \beta}{1+\tan \alpha \tan \beta}}}$

Podobnie otrzymujemy ze wzorów sinus i cosinus

${\ Displaystyle \ łóżeczko (\ alfa + \ beta) = {\ Frac {\ cos (\ alfa + \ beta)}} {\ sin (\ alfa + \ beta)}} = {\ Frac {\ cos \ alfa \ cos \beta -\sin \alpha \sin \beta }{\sin \alpha \cos \beta +\cos \alpha \sin \beta }}}$

Następnie dzieląc zarówno licznik, jak i mianownik przez ${\ Displaystyle \ sin \ alpha \ sin \ beta}$ , otrzymujemy

${\ Displaystyle \ łóżeczko (\ alfa + \ beta) = {\ Frac {\ łóżeczko \ alfa \ łóżeczko \ beta -1 }{\cot \alpha +\cot \beta }}}$

Lub używając ${\ Displaystyle \ łóżeczko \ theta = {\ Frac {1} {\ tan \ theta}}}$ ,

${\ Displaystyle \ łóżeczko (\ alfa + \ beta) = {\ Frac {1- \ tan \ alfa \ tan \ beta} {\ tan \ alfa + \ tan \ beta}} = {\ Frac {{\frac {1}{\tan \alpha \tan \beta}}-1}{{\frac {1}{\tan \alpha}}+{\frac {1}{\tan \beta}}} }={\frac {\cot \alpha \cot \beta -1}{\cot \alpha +\cot \beta }}}$

Używanie ${\ Displaystyle \ łóżeczko (- \ beta) = - \ łóżeczko \ beta}$ ,

${\ Displaystyle \ łóżeczko (\ alfa - \ beta) = {\ Frac {\ łóżeczko \ alfa \ łóżeczko (- \ beta) -1} {\ łóżeczko \ alfa + \ łóżeczko (- \ beta)}} = {\ frac {\cot \alpha \cot \beta +1}{\cot \beta -\cot \alpha }}}$

Tożsamości podwójnego kąta

Z kąta sumy tożsamości otrzymujemy

${\ Displaystyle \ sin (2 \ teta) = 2 \ grzech \ teta \ cos \ teta}$

I

${\ Displaystyle \ sałata (2 \ teta) = \ sałata ^ {2} \ teta - \ grzech ^ {2} \ teta}$

Tożsamości pitagorejskie dają dwie alternatywne formy dla tej ostatniej z nich:

${\ Displaystyle \ sałata (2 \ teta) = 2 \ sałata ^ {2} \ teta -1}$

${\ Displaystyle \ cos (2 \ teta) = 1-2 \ grzech ^ {2} \ teta}$

Tożsamości sumy kątów również dają

${\ Displaystyle \ dębnik (2 \ teta) = {\ Frac {2 \ tan \ teta} {1- \tan ^{2}\theta }}={\frac {2}{\cot \theta -\tan \theta }}}$

${\ Displaystyle \ łóżeczko (2 \ teta) = {\ Frac {\ łóżeczko ^ {2} \ teta -1} {2 \ łóżeczko \ teta}} = {\ Frac {\ łóżeczko \theta -\tan \theta }{2}}}$

Można to również udowodnić za pomocą wzoru Eulera

${\ Displaystyle e ^ {i \ varphi} = \ sałata \ varphi + i \ sin \ varphi}$

Podniesienie do kwadratu obu stron daje wyniki

${\ Displaystyle e ^ {i2 \ varphi} = (\ bo \ varphi + i \ sin \ varphi) ^ {2}}$

Ale zastąpienie kąta jego podwojoną wersją, która daje ten sam wynik po lewej stronie równania, daje wyniki

${\ Displaystyle e ^ {i2 \ varphi} = \ sałata 2 \ varphi + i \ sin 2 \ varphi}$

Wynika, że

${\ Displaystyle (\ cos \ varphi + i \ sin \ varphi) ^ {2} = \ sałata 2 \ varphi + i \ grzech 2\varphi}$ .

Rozwinięcie kwadratu i uproszczenie po lewej stronie równania daje

${\ Displaystyle i (2 \ sin \ varphi \ sałata \ varphi) + \ sałata ^ {2}\varphi -\sin ^{2}\varphi \ =\cos 2\varphi +i\sin 2\varphi}$ .

Ponieważ części urojone i rzeczywiste muszą być takie same, pozostaje nam oryginalna tożsamość

${\ Displaystyle \ sałata ^ {2} \ varphi - \ grzech ^ {2} \ varphi \ = \ sałata 2 \ varphi}$ ,

i również

${\ Displaystyle 2 \ sin \ varphi \ cos \ varphi = \ grzech 2 \ varphi}$ .

Tożsamości półkątowe

Dwie tożsamości dające alternatywne formy cos 2θ prowadzą do następujących równań:

${\ Displaystyle \ sałata {\ Frac {\ teta} {2}} = \ pm \, {\ sqrt {\ Frac {1 + \ cos \ teta} {2 }}},}$

${\ Displaystyle \ sin {\ Frac {\ teta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ teta} {2}}}.}$

Znak pierwiastka kwadratowego musi być odpowiednio dobrany — zwróć uwagę, że jeśli do θ dodamy 2 π , to wielkości wewnątrz pierwiastków pozostaną niezmienione, ale lewa strona równań zmieni znak. Dlatego właściwy znak do użycia zależy od wartości θ.

Dla funkcji tan równanie jest następujące:

${\ Displaystyle \ tan {\ Frac {\ theta} {2}} = \ pm \, {\ sqrt {\ Frac {1- \ cos \ theta} {1+ \ cos \ theta}}}.}$

Następnie pomnożenie licznika i mianownika wewnątrz pierwiastka kwadratowego przez (1 + cos θ) i użycie tożsamości pitagorejskich prowadzi do:

${\ Displaystyle \ tan {\ Frac {\ teta} {2}} = {\ Frac {\ sin \ teta} {1+ \ cos \ teta}}.}$

Ponadto, jeśli zarówno licznik, jak i mianownik zostaną pomnożone przez (1 - cos θ), wynik jest następujący:

${\ Displaystyle \ tan {\ Frac {\ theta} {2}} = {\ Frac {1- \ cos \ theta} {\ sin \ theta}}.}$

Daje to również:

${\ Displaystyle \ tan {\ Frac {\ teta} {2}} = \ csc \ teta - \ łóżeczko \ teta.}$

Podobne manipulacje dla funkcji łóżeczka dają:

${\ Displaystyle \ łóżeczko {\ Frac {\ theta} {2}} = \ pm \, {\ sqrt {\ Frac {1 + \ cos \ theta}} {1- \ cos \ theta}}} = {\ frac { 1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta .}$

Różne - potrójna tożsamość styczna

ψ ${\ Displaystyle \ psi + \ theta + \ phi = \ pi =}$ (na przykład i ${\ Displaystyle \ psi}$ , ${\ Displaystyle \ theta}$ i ${\ displaystyle \phi }$ to kąty trójkąta),

${\ Displaystyle \ tan (\ psi) + \ tan (\ teta) + \ tan (\ fi) = \ tan (\ psi) \ tan (\ teta) \ tan (\ fi).}$

Dowód:

${\ Displaystyle {\ rozpocząć {wyrównane} \ psi & = \ pi - \ theta - \ phi \\\ tan (\ psi) & = \ tan (\ pi - \ theta - \ phi) \\& = - \ tan (\theta +\phi )\\&={\frac {-\tan \theta -\tan \phi }{1-\tan \theta \tan \phi }}\\&={\frac {\tan \ theta +\tan \phi }{\tan \theta \tan \phi -1}}\\(\tan \theta \tan \phi -1)\tan \psi &=\tan \theta +\tan \phi \ \\tan \psi \tan \theta \tan \phi -\tan \psi &=\tan \theta +\tan \phi \\\tan \psi \tan \theta \tan \phi &=\tan \psi + \tan \theta +\tan \phi \\\end{wyrównane}}}$

Różne - potrójna tożsamość cotangensa

Jeśli ${\ Displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}} =}$ ćwiartka koła,

${\ Displaystyle \ łóżeczko (\ psi) + \ łóżeczko (\ theta) + \cot(\phi)=\cot(\psi)\cot(\theta)\cot(\phi)}$ .

Dowód:

Zastąp każdy z ich $kątami dopełniającymi$ , aby $cotangenty zamieniły$ w $styczne$ odwrotnie

Dany

${\ Displaystyle \ psi + \ teta + \ phi = {\ tfrac {\ pi} {2}}}$

${\ Displaystyle \ dlatego ({\ tfrac {\ pi}} {2}} - \ psi) + ({\ tfrac {\ pi} {2}} - \ theta) + ({\ tfrac {\ pi}} 2}}-\phi )={\tfrac {3\pi }{2}}-(\psi +\theta +\phi )={\tfrac {3\pi}}{2}}-{\tfrac {\ pi }{2}}=\pi }$

więc wynik wynika z potrójnej tożsamości stycznej.

Suma do tożsamości produktów

• ${\ Displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ lewo ({\ Frac {\ theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}$
• ${\ Displaystyle \ sałata \ teta + \ sałata \ fi = 2 \ sałata \ lewo ({\ Frac {\ teta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}$
• ${\ Displaystyle \ sałata \ teta - \ sałata \ fi = - 2 \ grzech \ lewo ({\ Frac { \theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)}$

Dowód tożsamości sinusoidalnych

Najpierw zacznij od tożsamości kąta sumy:

${\ Displaystyle \ sin (\ alfa + \ beta) = \ sin \ alfa \ sałata \ beta + \ sałata \ alfa \ grzech \ beta }$

${\ Displaystyle \ sin (\ alfa - \ beta) = \ sin \ alfa \ cos \ beta - \ cos \ alfa \ sin \ beta}$

Dodając je do siebie,

${\ Displaystyle \ sin (\ alfa + \ beta) + \ sin (\ alfa - \ beta) = \ sin \ alfa \ cos \ beta + \ cos \ alfa \ sin \ beta + \ sin \ alfa \ cos \ beta - \cos \alpha \sin \beta =2\sin \alpha \cos \beta }$

Podobnie, odejmując dwie tożsamości sumy kątów,

${\ Displaystyle \ sin (\ alfa + \ beta) - \ sin (\ alfa - \ beta) = \ sin \ alfa \ cos \ beta + \ cos \ alfa \ sin \ beta - \ sin \ alfa \ cos \ beta + \cos \alpha \sin \beta =2\cos \alpha \sin \beta }$

Niech ${\ Displaystyle \ alfa + \ beta = \ teta}$ i ${\ Displaystyle \ alfa - \ beta = \ phi}$ ,

${\ Displaystyle \ dlatego \ alfa = {\ Frac {\ teta + \ phi} {2}}}$ i ${\ Displaystyle \ beta = {\ Frac {\ theta - \fi }{2}}}$

Zastąp i ${\ Displaystyle \ theta}$ i ${\ Displaystyle \ phi}$

${\ Displaystyle \ sin \ teta + \ sin \ phi = 2 \ sin \ lewo ({\ Frac {\ teta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}$

${\ Displaystyle \ sin \ theta - \ sin \ phi = 2 \ sałata \ lewo ({\ Frac { \theta +\phi }{2}}\right)\sin \left({\frac {\theta -\phi }{2}}\right)=2\sin \left({\frac {\theta -\ phi }{2}}\right)\cos \left({\frac {\theta +\phi }{2}}\right)}$

Dlatego,

${\ Displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ lewo ({\ Frac {\ theta \pm \phi }{2}}\right)\cos \left({\frac {\theta \mp \phi }{2}}\right)}$

Dowód tożsamości cosinusowych

Podobnie w przypadku cosinusa, zacznij od tożsamości sumy kątów:

${\ Displaystyle \ sałata (\ alfa + \ beta) = \ sałata \ alfa \ sałata \ beta \ - \ grzech \ alfa \ grzech \beta }$

${\ Displaystyle \ cos (\ alfa - \ beta) = \ cos \ alfa \ cos \ beta + \ sin \ alfa \ sin \ beta}$

Znowu przez dodawanie i odejmowanie

${\ Displaystyle \ cos (\ alfa + \ beta) + \ cos (\ alfa - \ beta) = \ cos \ alfa \ cos \ beta \ - \ sin \ alfa \ sin \ beta + \ cos \ alfa \ cos \ beta +\sin \alpha \sin \beta$

${\ Displaystyle \ sałata (\ alfa + \ beta) - \ sałata (\ alfa - \ beta) = \ sałata \ alfa \ sałata \ beta \ - \ grzech \alpha \sin \beta -\cos \alpha \cos \beta -\sin \alpha \sin \beta =-2\sin \alpha \sin \beta }$

$2\cos \alpha \cos \beta }$

Zastąp i ${\ displaystyle \ theta}$ i ${\ displaystyle \ phi}$ jak poprzednio, θ {\ displaystyle \ theta}

${\ Displaystyle \ sałata \ teta + \ sałata \ fi = 2 \ sałata \ lewo ({\ Frac {\ teta +\phi }{2}}\right)\cos \left({\frac {\theta -\phi }{2}}\right)}$

${\ Displaystyle \ cos \ teta - \ cos \ phi = - 2 \ sin \ lewo ({\ Frac {\ teta + \ phi} {2}} \ prawej) \ sin \ lewo({\frac {\theta -\fi}} {2}}\prawo)}$

nierówności

Zobacz też: Lista nierówności trójkąta

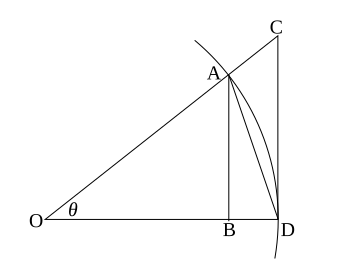
Ilustracja nierówności sinusoidalnych i stycznych.

Rysunek po prawej stronie przedstawia wycinek koła o promieniu 1. Wycinek to θ /(2 π ) całego koła, więc jego pole wynosi θ /2 . Zakładamy tutaj, że θ < π /2 .

$= OD = 1}$

${\ Displaystyle CD = \ tan \ theta}$

${\ Displaystyle AB = \ sin \ theta}$

Pole trójkąta OAD to AB /2 , czyli sin( θ )/2 . Pole trójkąta OCD to CD /2 , czyli tan( θ )/2 .

Ponieważ trójkąt OAD leży całkowicie wewnątrz sektora, który z kolei leży całkowicie wewnątrz trójkąta OCD , mamy

${\ Displaystyle \ sin \ teta <\ teta <\ tan \ teta.}$

Ten argument geometryczny opiera się na definicjach długości łuku i pola , które działają jako założenia, więc jest raczej warunkiem narzuconym w konstrukcji funkcji trygonometrycznych niż właściwością do udowodnienia. W przypadku funkcji sinus możemy obsłużyć inne wartości. Jeśli θ > π /2 , to θ > 1 . Ale grzech θ ≤ 1 (ze względu na tożsamość pitagorejską), więc grzech θ < θ . Więc mamy

${\ Displaystyle {\ Frac {\ sin \ theta} {\ theta} <1 \ \ \ \ operatorname {if} \ \ \ 0 <\ theta.}$

Dla ujemnych wartości θ mamy, z symetrii funkcji sinus

${\ Displaystyle {\ Frac {\ sin \ teta} {\ teta}} = {\ Frac {\ sin (- \ teta)}} {- \ teta }}<1.}$

Stąd

${\ Displaystyle {\ Frac {\ sin \ teta} {\ teta} <1 \ quad {\ tekst {jeśli}} \ quad \ teta \ neq 0,}$

I

${\ Displaystyle {\ Frac {\ tan \ teta} {\ teta}}> 1 \ quad {\ tekst {jeśli}} \ quad 0 <\ teta <{\ Frac {\ pi} {2}}.}$

Tożsamości z udziałem rachunku różniczkowego

Czynności wstępne

${\ Displaystyle \ lim _ {\ teta \ do 0} {\ sin \ teta} = 0}$

${\ Displaystyle \ lim _ {\ teta \ do 0} {\cos \theta}=1}$

Tożsamość stosunku sinusa i kąta

${\ Displaystyle \ lim _ {\ teta \ do 0} {\ Frac {\ sin \ teta} {\ teta}} = 1}$

Innymi słowy, funkcja sinus jest różniczkowalna w punkcie 0, a jej pochodna wynosi 1.

Dowód: Z poprzednich nierówności mamy dla małych kątów

${\ Displaystyle \ sin \ teta <\ teta <\ tan \ teta}$ ,

Dlatego,

${\ Displaystyle {\ Frac {\ sin \ teta}} {\ teta} <1 <{\ Frac {\ tan \ teta} {\ teta}}}$ ,

Rozważ prawą nierówność. Od

${\ Displaystyle \ dębnik \ teta = {\ Frac {\ sin \ teta} {\ sałata \ teta}}}$

${\ Displaystyle \ dlatego 1<{\frac {\sin \theta}} {\theta \cos \theta}}}$

Pomnóż przez ${\ Displaystyle \ cos \ theta}$

${\ Displaystyle \ sałata \ teta <{\ Frac {\ sin \ teta} {\ teta}}}$

Łącząc z nierównością po lewej stronie:

${\ Displaystyle \ sałata \ teta <{\ Frac {\ sin \ teta} {\ teta} <1}$

Biorąc ${\ Displaystyle \ cos \ theta}$ do granicy jako ${\ Displaystyle \ theta \ do 0}$

${\ Displaystyle \ lim _ {\ teta \ do 0} {\ cos \ teta} = 1}$

Dlatego,

${\ Displaystyle \ lim _ {\ teta \ do 0} {\ Frac {\ sin \ teta} {\ teta}} = 1}$

Tożsamość ilorazu cosinusa i kąta

${\ Displaystyle \ lim _ {\ teta \ do 0} {\ Frac {1- \ cos \ teta} {\ teta}} = 0}$

Dowód:

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {1- \ cos \ teta} {\ teta}} & = {\ Frac {1- \ cos ^ {2} \ teta}} {\ teta (1+ \cos \theta )}}\\&={\frac {\sin ^{2}\theta }{\theta (1+\cos \theta)}}\\&=\left({\frac {\sin \theta }{\theta }}\right)\times \sin \theta \times \left({\frac {1}{1+\cos \theta }}\right)\\\end{aligned}}}$

Granice tych trzech wielkości to 1, 0 i 1/2, więc wynikowa granica wynosi zero.

Cosinus i kwadrat tożsamości ilorazu kątów

${\ Displaystyle \ lim _ {\ teta \ do 0} {\ Frac {1- \ cos \ teta} {\ teta ^ {2}}} = {\ Frac {1}{2}}}$

Dowód:

Podobnie jak w poprzednim dowodzie,

${\ Displaystyle {\ Frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ Frac {\ sin \ theta} {\ theta}} \ razy {\ Frac {\ sin \ theta}} \theta }}\times {\frac {1}{1+\cos \theta}}.}$

Granice tych trzech wielkości to 1, 1 i 1/2, więc wynikowa granica to 1/2.

Dowód złożenia funkcji trygonometrycznych i odwrotnych funkcji trygonometrycznych

Wszystkie te funkcje wynikają z tożsamości trygonometrycznej Pitagorasa. Możemy na przykład udowodnić funkcję

${\ Displaystyle \ sin [\ arctan (x)] = {\ Frac {x} {\ sqrt {1 + x ^ {2}}}}}$

Dowód:

Zaczynamy od

${\ Displaystyle \ sin ^ {2} \ teta + \ sałata ^ {2} \ teta = 1}$ (ja)

Następnie dzielimy to równanie (I) przez ${\ Displaystyle \ cos ^ {2} \ theta}$

${\ Displaystyle \ sałata ^ {2} \ teta = {\ Frac {1} {\ dębnik ^ {2} \ teta + 1}}}$ (II)

${\ Displaystyle 1- \ grzech ^ {2} \ teta = {\ Frac {1} {\ tan ^ {2} \ teta + 1}}}$

Następnie użyj podstawienia ${\ Displaystyle \ theta = \ arctan (x)}$ :

${\ Displaystyle 1- \ sin ^ {2} [\ arctan (x)] = {\ Frac {1 }{\ tan ^ {2}[\ arctan(x)]+1}}}$

${\ Displaystyle \ sin ^ {2} [\ arctan (x)] = {\ Frac {\ tan ^ {2} [\ arctan (x)]} {\tan ^{2}[\arctan(x)]+1}}}$

Następnie używamy tożsamości ${\ Displaystyle \ tan [\ arctan (x)] \ równoważnik x}$

${\ Displaystyle \ sin [\ arctan (x)] = {\ Frac {x} {\ sqrt {x ^ {2} + 1}}}}$ ( II)

I potwierdzono początkową tożsamość trygonometryczną Pitagorasa...

Podobnie, jeśli podzielimy to równanie (I) przez ${\ Displaystyle \ sin ^ {2} \ theta}$

${\ Displaystyle \ sin ^ {2} \ teta = {\ Frac {\ Frac {1} {1}}} {1 + {\ Frac {1} {\ dębnik ^ {2} \ teta}}}}}$ (II)

${\ Displaystyle \ sin ^ {2} \ teta = {\ Frac {\ dębnik ^ { 2}\theta }{\tan ^{2}\theta +1}}}$

Następnie użyj podstawienia ${\ Displaystyle \ theta = \ arctan (x)}$ :

${\ Displaystyle \ sin ^ {2} [\ arctan (x)] = {\frac {\tan ^{2}[\arctan(x)]}{\tan ^{2}[\arctan(x)]+1}}}$

Następnie używamy tożsamości ${\ Displaystyle \ tan [\ arctan (x)] \ równoważnik x}$

${\ Displaystyle \ sin [\ arctan (x)] = {\ Frac {x} {\ sqrt {x ^ {2} + 1}}}}$ ( II)

I potwierdzono początkową tożsamość trygonometryczną Pitagorasa...

${\ Displaystyle [\ arctan (x)] = [\ arcsin ({\ Frac {x} {\ sqrt {x ^ {2} + 1}}})]}$

${\ Displaystyle y = {\ Frac {x} {\ sqrt {x ^ {2} + 1}}}}$

${ \ Displaystyle y ^ {2} = {\ frac {x ^ {2}} {x ^ {2} + 1}}}$ (IV)

Zgadnijmy, że mamy do udowodnienia:

${\ Displaystyle x = {\ Frac {y} {\ sqrt {1-y ^ {2}}}}}$

${\ displaystyle x ^ {2} ={\frac {y^{2}}{1-y^{2}}}}$ (V)

Zamiana (V) na (IV):

${\ Displaystyle y ^ {2} = {\ Frac {\ Frac {y ^ {2}} {(1-y ^ { 2})}}{{\frac {y^{2}}{(1-y^{2})}}+1}}}$

${\ Displaystyle y ^ {2} = {\ Frac {\ Frac {y ^ {2}} {(1-y ^ {2})}} {\ Frac {1} {(1-y ^ {2} )}}}}$

Więc to prawda: ${\ Displaystyle y ^ {2} = y ^ {2}}$ i zgadywanie było prawdziwe: ${\ Displaystyle x = {\ Frac {y} {\ sqrt {1-y^{2}}}}}$

${\ Displaystyle [\ arctan (x)] = [\arcsin({\frac {x}{\sqrt {x^{2}+1}}})]=[\arcsin(y)]=[\arctan({\frac {y}{\sqrt {1 -y^{2}}}})]}$

Teraz y można zapisać jako x; i mamy [arcsin] wyrażone przez [arctan]…

${\ Displaystyle [\ arcsin (x)] = [\ arctan ({\ Frac {x} {\ sqrt {1-x ^ {2 }}}})]}$

Podobnie, jeśli szukamy : ${\ Displaystyle [\ arccos (x)]}$ ...

${\ Displaystyle \ sałata [\ arccos (x)] = x}$

${\ Displaystyle \cos({\frac {\pi }{2}}-({\frac {\pi }{2}}-[\arccos(x)]))=x}$

${\ Displaystyle \ sin ({\ Frac {\ pi} {2}} - [\ arccos (x)]) = x}$

${\ Displaystyle {\ Frac {\ pi} {2}} - [\ arccos (x)] = [\ arcsin (x)]}$

${\ Displaystyle [\ arccos (x)] = {\ Frac {\ pi} {2}} - [\ arcsin (x)]}$

od : ${\ Displaystyle [\ arcsin (x)]}$ ...

${\ Displaystyle [\ arccos (x)] = {\ Frac {\ pi} {2}} - [\ arctan ({{ \frac {x}{\sqrt {1-x^{2}}}})]}$

${\ Displaystyle [\ arccos (x)] = {\ Frac {\ pi} {2}} - [\ operatorname {arccot} ({\ Frac {\ sqrt {1-x ^ {2}}} {x}} )]}$

I wreszcie mamy [arccos] wyrażone przez [arctan]…

${\ Displaystyle [\ arccos (x)] = [\ arctan ({\ Frac {\ sqrt {1-x ^ {2}}} {X}})]}$

Zobacz też

• Lista tożsamości trygonometrycznych
• Formuła przybliżenia sinusoidalnego Bhaskary I
• Generowanie tablic trygonometrycznych
• Tabela sinusów Aryabhaty
• Tabela sinusów Madhawy
• Tabela szeregów Newtona
• Seria Madhawa
• Wektor jednostkowy (wyjaśnia cosinusy kierunku)
• Formuła Eulera

Notatki

• ET Whittaker i GN Watson . Kurs nowoczesnej analizy , Cambridge University Press , 1952