Dwuścienna grupa rzędu 6

Wykres Cayleya z permutacjami trójkąta

Wykres cyklu z macierzami permutacji 3 elementów (Generatory a i b są takie same jak na powyższym wykresie Cayleya).

Tablica Cayleya jako tabliczka mnożenia macierzy permutacji

Pozycje sześciu elementów w tabeli Cayleya Tylko elementy neutralne są symetryczne względem głównej przekątnej, więc ta grupa nie jest abelowa .

Tabela Cayleya jako ogólna (i specjalna ) grupa liniowa GL(2, 2)

W matematyce D _{3 (czasami} S _{alternatywnie} oznaczane jako D ₆ ) jest grupą dwuścienną stopnia 3 i rzędu 6. Jest równa grupie symetrycznej 3 . Jest to również najmniejsza grupa nieabelowa .

Ta strona ilustruje wiele koncepcji grup na przykładzie tej grupy.

Grupy symetrii

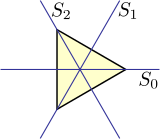
Grupa dwuścienna D ₃ jest grupą symetrii trójkąta równobocznego , to jest zbiorem wszystkich przekształceń, takich jak odbicie, obrót i ich kombinacje, które pozostawiają stały kształt i położenie tego trójkąta. W przypadku D ₃ każda możliwa permutacja wierzchołków trójkąta stanowi takie przekształcenie, że grupa tych symetrii jest izomorficzna z grupą symetryczną S ₃ wszystkich permutacji trzech różnych elementów. Nie dotyczy to grup dwuściennych wyższych rzędów.

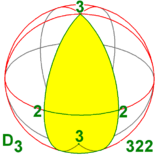
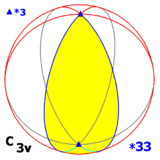
Grupa dwuścienna D ₃ jest izomorficzna z dwiema innymi grupami symetrii w trzech wymiarach:

• jeden z 3-krotną osią obrotu i prostopadłą 2-krotną osią obrotu (stąd trzy z nich): D ₃
• jeden z 3-krotną osią obrotu w płaszczyźnie odbicia (a więc także w dwóch innych płaszczyznach odbicia): C _3v

Permutacje zbioru trzech obiektów

Rozważmy trzy kolorowe bloki (czerwony, zielony i niebieski), początkowo ułożone w kolejności RGB. Grupa symetryczna S ₃ jest więc grupą wszystkich możliwych przegrupowań tych bloków. Jeśli przez a oznaczymy akcję „zamień dwa pierwsze bloki”, a przez b akcję „zamień dwa ostatnie bloki”, możemy zapisać wszystkie możliwe permutacje w kategoriach tych dwóch akcji.

W formie multiplikatywnej tradycyjnie piszemy xy dla połączonej akcji „najpierw zrób y , potem zrób x ”; więc ab jest akcją RGB ↦ RBG ↦ BRG , tj. „weź ostatni klocek i przesuń go na przód”. Jeśli napiszemy e dla „ pozostaw bloki takimi, jakie są” (akcja tożsamości), możemy zapisać sześć permutacji zestawu trzech bloków jako następujące akcje:

• e : RGB ↦ RGB lub ()
• a : RGB ↦ GRB lub (RG)
• b : RGB ↦ RBG lub (GB)
• ab : RGB ↦ BRG lub (RGB)
• ba : RGB ↦ GBR lub (RBG)
• aba : RGB ↦ BGR lub (RB)

Notacja w nawiasach to notacja cyklu .

Zauważ, że akcja aa daje efekt RGB ↦ GRB ↦ RGB , pozostawiając bloki bez zmian; więc możemy napisać aa = e . Podobnie,

• bb = e ,
• ( aba ) ( aba ) = mi , i
• ( ab ) ( ba ) = ( ba ) ( ab ) = mi ;

więc każde z powyższych działań ma odwrotność.

Poprzez inspekcję możemy również określić asocjatywność i zamknięcie (dwa z niezbędnych aksjomatów grupowych ); zauważ np

• ( ab ) za = za ( ba ) = aba , i
• ( ba ) b = b ( ab ) = bab .

Grupa nie jest abelowa, ponieważ na przykład ab ≠ ba . Ponieważ jest zbudowany z działań podstawowych a i b , mówimy, że generuje go zbiór { a , b } .

Grupa ma prezentację

${\ Displaystyle \ langle r, a \ mid r ^ {3} = 1, a ^ {2} = 1, ara = r ^ {- 1} \ rangle }$ , również napisane ${\ Displaystyle \ langle r, a \ mid r ^ {3}, a ^ {2} arar \ rangle}$

lub

${\ Displaystyle \ langle a, b \ mid a ^ {2} = b ^ {2} = (ab) ^ {3} = 1 \ rangle}$ , również napisane ${\ Displaystyle \ langle a, b \ mid a ^ {2}, b ^ {2} ,(ab)^{3}\rangle }$

gdzie aib to zamiany, a r = ab to cykliczna permutacja. Zauważ, że druga prezentacja oznacza, że ​​grupa jest grupą Coxetera . (W rzeczywistości wszystkie grupy dwuścienne i symetrii są grupami Coxetera).

Podsumowanie operacji grupowych

Za pomocą generatorów a i b definiujemy dodatkowe skróty c := aba , d := ab i f := ba , tak że a, b, c, d, e i f są elementami tej grupy. Możemy następnie podsumować operacje grupowe w postaci tabeli Cayleya :

*	mi	A	B	C	D	F
mi	mi	A	B	C	D	F
A	A	mi	D	F	B	C
B	B	F	mi	D	C	A
C	C	D	F	mi	A	B
D	D	C	A	B	F	mi
F	F	B	C	A	mi	D

Zauważ, że nierówne elementy niebędące tożsamościami dojeżdżają do pracy tylko wtedy, gdy są wzajemnie odwrotne. Dlatego grupa jest bezśrodkowa , tzn. centrum grupy składa się tylko z elementu tożsamości.

Klasy koniugacji

Możemy łatwo rozróżnić trzy rodzaje permutacji trzech bloków, klas koniugacji grupy:

• bez zmian (), element grupowy rzędu 1
• zamiana dwóch bloków: (RG), (RB), (GB), trzy elementy grupowe rzędu 2
• cykliczna permutacja wszystkich trzech bloków: (RGB), (RBG), dwa elementy grupowe rzędu 3

Na przykład (RG) i (RB) mają postać ( x y ); permutacja liter R, G i B (mianowicie (GB)) zmienia notację (RG) na (RB). Dlatego jeśli zastosujemy (GB), następnie (RB), a następnie odwrotność (GB), która jest również (GB), wynikowa permutacja to (RG).

Należy zauważyć, że sprzężone elementy grupy mają zawsze tę samą kolejność , ale generalnie dwa elementy grupy, które mają tę samą kolejność, nie muszą być sprzężone.

Podgrupy

Z twierdzenia Lagrange'a wiemy, że każda nietrywialna podgrupa grupy z 6 elementami musi mieć rząd 2 lub 3. W rzeczywistości dwie cykliczne permutacje wszystkich trzech bloków, z tożsamością, tworzą podgrupę rzędu 3, indeks 2 i zamiany dwóch bloków, każdy z tożsamością, tworzą trzy podgrupy rzędu 2, indeks 3. Istnienie podgrup rzędu 2 i 3 jest również konsekwencją twierdzenia Cauchy'ego .

Pierwszą wymienioną jest {() _, (RGB), (RBG)}, grupa naprzemienna A3 .

Lewe coset i prawe coset A ₃ pokrywają się (tak jak dla dowolnej podgrupy indeksu 2) i składają się z A ₃ i zbioru trzech zamian { (RB), (RG), (BG) }.

Lewe cosets { (), (RG) } to:

• { (), (RG)}
• { (RB), (RGB) }
• { (GB), (RBG) }

Odpowiednie zbiory { (RG), () } to:

• { (RG), () }
• { (RBG), (RB) }
• { (RGB), (GB) }

Zatem A ₃ jest normalne , a pozostałe trzy nietrywialne podgrupy nie. Grupa ilorazowa G / A ₃ jest izomorficzna z C ₂ .

${\ Displaystyle G = \ operatorname {A} _ {3} \ rtimes H}$ , produkt półbezpośredni , gdzie H jest podgrupą dwóch elementów: () i jednej z trzech zamian. Ten rozkład jest również konsekwencją (przypadek szczególny) twierdzenia Schura – Zassenhausa .

Pod względem permutacji dwa elementy grupowe G /A ₃ to zbiór permutacji parzystych i zbiór permutacji nieparzystych.

Jeśli oryginalna grupa jest generowana przez obrót płaszczyzny o 120 ° wokół punktu i odbicie względem linii przechodzącej przez ten punkt, to grupa ilorazowa ma dwa elementy, które można opisać jako podzbiory „po prostu obróć ( albo nic nie rób)” i „zrób lustrzane odbicie ”.

Zauważmy, że dla grupy symetrii kwadratu nierówna permutacja wierzchołków nie odpowiada wykonaniu odbicia lustrzanego, ale operacji niedozwolonej dla prostokątów , czyli obróceniu o 90° i zastosowaniu diagonalnej osi odbicia.

Produkty półbezpośrednie

$\ Displaystyle \ operatorname {C} _ {3} \ rtimes _ {\ varphi} \ operatorname {C} _ {2}}$ jest $\ Displaystyle \ operatorname {C} _ {3}\times \mathrm {C} _{2}}$ jeśli zarówno φ (0), jak i φ (1) są tożsamościami. Iloczyn półprosty jest izomorficzny z grupą dwuścienną rzędu 6, jeśli φ (0) jest tożsamością, a φ (1) jest nietrywialnym automorfizmem C ₃ , który odwraca elementy.

W ten sposób otrzymujemy:

( n ₁ , 0) * ( n ₂ , godz ₂ ) = ( n ₁ + n ₂ , godz ₂ )

( n ₁ , 1) * ( n ₂ , godz ₂ ) = ( n ₁ - n ₂ , 1 + godz ₂ )

dla wszystkich n ₁ , n ₂ w C ₃ i h ₂ w C ₂ . Bardziej zwięźle,

${\ Displaystyle (n_ {1}, h_ {1}) * (n_{2},h_{2})=(n_{1}+(-1)^{h_{1}}n_{2},h_{1}+h_{2})}$

dla wszystkich n ₁ , n ₂ w C ₃ i h ₁ , h ₂ w C ₂ .

W tabeli Cayleya:

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

Zauważ, że dla drugiej cyfry zasadniczo mamy tabelę 2×2, z równymi wartościami 3×3 dla każdej z tych 4 komórek. Dla pierwszej cyfry lewa połowa tabeli jest taka sama jak prawa, ale górna połowa różni się od dolnej.

Dla iloczynu bezpośredniego tabela jest taka sama, z wyjątkiem tego, że pierwsze cyfry dolnej połowy tabeli są takie same jak w górnej połowie.

Akcja grupowa

Rozważ D ₃ w sposób geometryczny, jako grupę symetrii izometrii płaszczyzny i rozważ odpowiednie działanie grupowe na zbiorze 30 równomiernie rozmieszczonych punktów na okręgu, ponumerowanych od 0 do 29, z 0 na jednej z osi odbicia .

Ta sekcja ilustruje koncepcje działań grupowych dla tej sprawy.

Działanie G na X nazywa się

• przechodnia , jeśli dla dowolnych dwóch x , y w X istnieje g w G takie, że g · x = y ; nie o to chodzi
• wierny (lub efektywny ), jeśli dla dowolnych dwóch różnych g , h w G istnieje x w X takie, że g · x ≠ h · x ; tak jest, ponieważ poza tożsamością grupy symetrii nie zawierają elementów, które „nic nie robią”
• wolny , jeśli dla dowolnych dwóch różnych g , h w G i wszystkich x w X mamy g · x ≠ h · x ; tak nie jest, ponieważ istnieją refleksje

Orbity i stabilizatory

Orbity 30 równomiernie rozmieszczonych punktów na okręgu pod działaniem grupowym D ₃

Orbita punktu x w X jest zbiorem elementów X , do których x może być przesunięty przez elementy G . Orbita x jest oznaczona przez Gx :

${\ Displaystyle Gx = \ lewo \ {g \ cdot x \ środkowy g \ w G \ prawo \}}$

Orbity to {0, 10, 20}, {1, 9, 11, 19, 21, 29}, {2, 8, 12, 18, 22, 28}, {3, 7, 13, 17, 23, 27}, {4, 6, 14, 16, 24, 26} i {5, 15, 25}. Punkty na orbicie są „równoważne”. Jeśli grupa symetrii ma zastosowanie do wzoru, to w obrębie każdej orbity kolor jest taki sam.

Zbiór wszystkich orbit X pod działaniem G jest zapisany jako X / G .

Jeśli Y jest podzbiorem X { g · y : y ∈ Y i , ∈ G }. Podzbiór zapisujemy GY dla zbioru g Y nazywamy niezmiennikiem G, jeśli GY = Y (co jest równoważne GY ⊆ Y ) . W takim przypadku G działa również na Y . Podzbiór Y nazywamy ustalonym pod G , jeśli g · y = y dla wszystkich g w G i wszystkich y w Y. Suma np. dwóch orbit jest niezmienna pod G , ale nie jest ustalona.

Dla każdego x w X definiujemy podgrupę stabilizatora x ( zwaną także grupą izotropową lub małą grupą ) jako zbiór wszystkich elementów w G , które ustalają x :

${\ Displaystyle G_ {x} = \ {g \ w G \ mid g \ cdot x = x \}}$

Jeśli x jest punktem odbicia (0, 5, 10, 15, 20 lub 25) , jego stabilizatorem jest grupa drugiego rzędu zawierająca tożsamość i odbicie w x . W innych przypadkach stabilizatorem jest grupa trywialna.

Dla ustalonego x w X , rozważmy mapę od G do X określoną przez g ↦ g · x . Obrazem mapy x _jest orbita x , a współobrazem jest zbiór wszystkich lewych cosetów G . Standardowe twierdzenie ilorazowe teorii mnogości daje wtedy naturalną bijekcję między G / G _x i Gx . Konkretnie, bijekcja jest dana przez hG _x ↦ h · x . Wynik ten jest znany jako twierdzenie o stabilizatorze orbity . W dwóch przypadkach małej orbity stabilizator jest nietrywialny.

Jeśli dwa elementy x i y należą do tej samej orbity, to ich podgrupy stabilizatorów, G _x i G _y , są izomorficzne . Dokładniej: jeśli y = g · x , to G _y = gG _x g ⁻¹ . W przykładzie dotyczy to np. 5 i 25, obu punktów odbicia. Odbicie o 25 odpowiada obrocie o 10, odbiciu o 5 i obrocie o -10.

Wynikiem ściśle związanym z twierdzeniem o stabilizatorze orbity jest lemat Burnside'a :

${\ Displaystyle \ lewo | X/G \ prawo | = {\ Frac {1} {\ lewo | G \ prawo |}} \ suma _ {g \ in G} \ lewo | X ^ {g} \ prawo |}$

gdzie X ^g jest zbiorem punktów ustalonych przez g . Oznacza to, że liczba orbit jest równa średniej liczbie punktów ustalonych na element grupy.

Dla tożsamości wszystkie 30 punktów jest stałych, dla dwóch obrotów żadnego, a dla trzech odbić po dwa: {0, 15}, {5, 20} i {10, 25}. Zatem średnia wynosi sześć, liczba orbit.

Teoria reprezentacji

Aż do izomorfizmu grupa ta ma trzy nieredukowalne złożone reprezentacje jednostkowe, które będziemy nazywać $ρ$ reprezentacja trywialna), i $\ displaystyle \ rho _ {1}}$ i ${\ displaystyle \ rho _ {2}}$ , gdzie indeks dolny wskazuje wymiar. Z definicji jako grupa permutacji na zbiorze z $,$ grupa ma reprezentację na poprzez wpisów wektora, podstawowej reprezentacji. Ta reprezentacja nie jest $displaystyle \ rho _ {2}}$ , ponieważ rozkłada się jako bezpośrednia suma i $\$ . ${\ Displaystyle I}$ pojawia się jako podprzestrzeń wektorów postaci ${\ Displaystyle (\ lambda, \ lambda, \ lambda), \ lambda \ w \ mathbb {C}}$ ρ ${\ Displaystyle \ rho _ {2}}$ jest reprezentacją na jego dopełnieniu ortogonalnym, które są wektorami postaci $\ Displaystyle (\ lambda _ {1 },\lambda _{2},-\lambda _{1}-\lambda _{2})}$ . Nietrywialna jednowymiarowa reprezentacja powstaje w grupach $}$ : Akcja polega na mnożeniu przez znak permutacji ρ $\ Displaystyle \ rho _$ element grupy. Każda skończona grupa ma taką reprezentację, ponieważ przez swoje regularne działanie jest podgrupą grupy cyklicznej. $_$ reprezentacji _ zobacz, to muszą być wszystkie nieredukowalne reprezentacje.

Dwuwymiarowa nieredukowalna reprezentacja liniowa daje jednowymiarową reprezentację rzutową (tj. działanie na linii rzutowej , osadzenie w grupie Möbiusa PGL(2, C ) ), ponieważ transformaty eliptyczne . Można to przedstawić za pomocą macierzy z wpisami 0 i ±1 (tutaj zapisanych jako ułamkowe przekształcenia liniowe ), znanych jako grupa anharmoniczna :

• zamówienie 1: ${\ displaystyle z}$
• kolejność 2: ${\ Displaystyle 1-z, 1 / z, z / (z-1)}$
• kolejność 3: ${\ Displaystyle (z-1) / z, 1 / (1-z)}$

i w ten sposób schodzi do reprezentacji na dowolnym polu, która jest zawsze wierna/iniekcyjna (ponieważ żadne dwa terminy nie różnią się tylko znakiem). Na polu z dwoma elementami prosta rzutowa ma tylko 3 punkty, a więc jest to wyjątkowy izomorfizm ${\ Displaystyle S_ {3} \ około \ operatorname {PGL} (2,2).}$ W charakterystyce 3 to osadzenie stabilizuje punkt $,}$${\ Displaystyle -1 = [-1:$$permutowane$ ponieważ (w i są krzyżowego ) Nad polem z trzema elementami linia rzutowa ma 4 elementy, a ponieważ PGL (2, 3) jest izomorficzna z grupą symetryczną na 4 elementach, S ₄ , wynikowe osadzenie ${\ Displaystyle \ operatorname {S } _ {3} \ hookrightarrow \ operatorname {S} _ {4}}$ równa się stabilizatorowi punktu ${\ Displaystyle -1}$ .

Zobacz też

• Grupa dwuścienna rzędu 8

•   Fraleigh, John B. (1993), A First Course in Abstract Algebra (wyd. 5), Addison-Wesley, s. 93–94, ISBN 978-0-201-53467-2

Linki zewnętrzne

• http://mathworld.wolfram.com/DihedralGroupD3.html