Dziewięć lematów

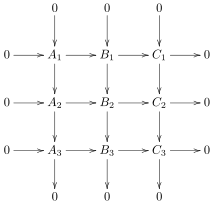
W matematyce lemat dziewięciu (lub lemat 3 × 3) jest stwierdzeniem o diagramach przemiennych i dokładnych ciągach ważnych w kategorii grup i dowolnej kategorii abelowej . Stwierdza: jeśli diagram po prawej stronie jest diagramem przemiennym i wszystkie kolumny oraz dwa dolne wiersze są dokładne, to górny rząd jest również dokładny. Podobnie, jeśli wszystkie kolumny oraz dwa górne wiersze są dokładne, dolny rząd również jest dokładny. Podobnie, ponieważ diagram jest symetryczny względem swojej przekątnej, wiersze i kolumny również mogą być zamieniane w powyższym.

Dziewięć lematów można udowodnić przez bezpośrednie ściganie diagramów lub zastosowanie lematu węża (do dwóch dolnych rzędów w pierwszym przypadku i do dwóch górnych rzędów w drugim przypadku).

Linderholm (s. 201) przedstawia satyryczny pogląd na dziewięć lematów:

„Narysuj tablicę z kółkiem i krzyżykiem … Nie wypełniaj jej kółkami i krzyżykami… Zamiast tego użyj zakrzywionych strzałek… Machaj rękami, wykonując skomplikowane wzory na tej planszy. Zrób kilka kółek, ale nie w kwadratach; umieść je na obu końcach poziomych i pionowych linii. Twórz twarze. Udowodniłeś teraz: (a) lemat o dziewięciu (b) lemat o szesnastce (c) lemat o dwudziestu

pięciu

…

”

Istnieją dwa warianty lematu o dziewięciu: lemat o dziewięciu ostrych i lemat o symetrycznych dziewięciu (patrz lematy 3.3, 3.4 w rozdziale XII).

•   Linderholm, Carl (1971). Matematyka stała się trudna . Wolfe'a. ISBN 0-7234-0415-1 .