Efekty nieliniowe

W syntezie enancjoselektywnej efekt nieliniowy odnosi się do procesu, w którym czystość enancjomeryczna katalizatora lub chiralnego środka pomocniczego nie odpowiada czystości enancjomerycznej wytworzonego produktu. Na przykład: racemiczny przekształci prochiralny substrat w produkt racemiczny (efekt liniowy), ale nie zawsze tak jest i zamiast tego można wytworzyć produkt wzbogacony chiralnie (efekt nieliniowy).

Można to wyrazić matematycznie , jak pokazano w równaniu 1. Stereoselekcja, która jest wyższa lub niższa niż nadmiar enancjomeryczny katalizatora, jest uważana za zachowanie nieidealne. W przypadku zachowania nieidealnego to odchylenie od liniowości jest opisywane jako efekt nieliniowy , NLE .

${\ displaystyle ee _ {\ tekst {produkt}} = ee _ {\ max} ee _ {\ tekst {katalizator}}}$

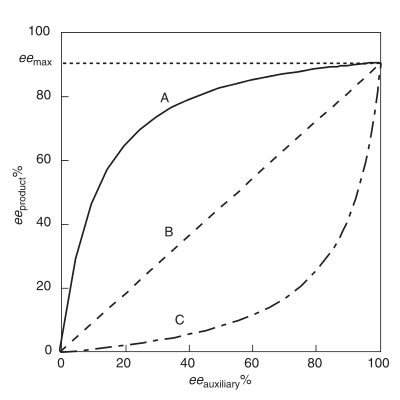
Dla idealnej reakcji asymetrycznej _produkt ee można opisać jako iloczyn ee _{max pomnożony przez katalizator} ee . Nie dotyczy to reakcji wykazujących NLE.

Efekty nieliniowe często pojawiają się w reakcjach ze skalemiczną kompozycją katalizatora. Jak po raz pierwszy zaobserwowali Wynberg i Feringa w 1976 r., różne enancjomery katalizatorów chiralnych tworzą kompleksy heterochiralne, a dokładniej agregaty wysokiego rzędu lub formy dimeryczne katalizatora. Te heterochiralne kompleksy wpływają na efektywną stereoindukcję katalizatora skalemicznego. Dodatkowe źródła efektów nieliniowych obejmują autokatalizę, proces, w którym reakcja katalizuje się. Ogólne definicje i modele matematyczne są kluczem do zrozumienia efektów nieliniowych i ich zastosowania w określonych reakcjach chemicznych. W ciągu ostatnich dwóch dekad badanie efektów nieliniowych wykazało, że wyjaśnia mechanizm reakcji i pomaga w zastosowaniach syntetycznych.

Rodzaje efektów nieliniowych

Zależność między _{produktem ee a katalizatorem} ee w scenariuszach (+) -NLE, liniowym i (-) -NLE.

Dodatni efekt nieliniowy, (+)-NLE

Dodatni efekt nieliniowy , (+)-NLE , występuje w reakcji asymetrycznej, która wykazuje wyższy produkt ee (iloczyn ee ₎ niż przewidywany przez idealną sytuację liniową (Rysunek 1). Jest często określany jako amplifikacja asymetryczna , termin ukuty przez Oguniego i współpracowników. Przykład pozytywnego efektu nieliniowego obserwuje się w przypadku epoksydacji Sharplessa z substratem geraniolem . We wszystkich przypadkach reaktywności chemicznej wykazującej (+) -NLE istnieje wrodzony kompromis między ogólną szybkością reakcji a enancjoselektywnością. Ogólna szybkość jest wolniejsza, a enancjoselektywność jest wyższa w stosunku do reakcji zachowującej się liniowo.

Ujemny efekt nieliniowy, (-)-NLE

Określany jako asymetryczne wyczerpywanie się , ujemny efekt nieliniowy występuje, gdy _{iloczyn ee} jest niższy niż przewidywany przez idealną sytuację liniową. W przeciwieństwie do (+)-NLE, (-)-NLE skutkuje większą ogólną szybkością reakcji i spadkiem enancjoselektywności. Syntetycznie, efekt (-)-NLE mógłby być korzystny przy rozsądnym teście do rozdzielania enancjomerów produktu i konieczna jest wysoka wydajność. Interesujący przykład efektu (-) -NLE odnotowano w asymetrycznych utlenianiach siarczków .

Modelowanie efektów nieliniowych

W 1986 roku Henri B. Kagan i współpracownicy zaobserwowali serię znanych reakcji, które następowały po nieidealnym zachowaniu. Współczynnik korygujący, f , został dostosowany do Równania 1, aby dopasować zachowanie kinetyczne reakcji z NLE (Równanie 2).

${\ displaystyle ee _ {\ tekst {produkt}} = f \, ee _ {\ max} ee _ {\ tekst {katalizator}}}$

Równanie 2: Ogólne równanie matematyczne opisujące zachowanie nieliniowe

Niestety, równanie 2 jest zbyt ogólne, aby można je było zastosować do konkretnych reakcji chemicznych. Z tego powodu Kagan i współpracownicy opracowali również uproszczone modele matematyczne opisujące zachowanie katalizatorów, które prowadzą do efektów nieliniowych. Modele te obejmują rodzajowe rodzaje ML _{n , oparte na} metalu (M) związanym z liczbą n ligandów enancjomerycznych (L). Typ ML n różni się w zależności od reakcji asymetrycznych, w oparciu o dobroć dopasowania z danymi reakcji. Dzięki dokładnemu modelowaniu NLE może wyjaśnić mechanistyczne szczegóły enancjoselektywnej reakcji katalitycznej.

Model ML2 _{_}

Ogólny opis

Najprostszy model opisujący efekt nieliniowy, model ML ₂ obejmuje układ metali (M) z dwoma chiralnymi ligandami, _LR i _LS . Oprócz katalizowanej reakcji będącej przedmiotem zainteresowania model uwzględnia równowagę w stanie ustalonym między niezwiązanymi i związanymi kompleksami katalizatorów. Istnieją trzy możliwe kompleksy katalityczne w stanie równowagi (ML _S L _R , ML _S L _S , ML _R L _R ). Dwa enancjomerycznie czyste kompleksy ( ML _{SLS ,} ML _R L _R ) są określane jako kompleksy homochiralne . Możliwy kompleks heterochiralny ML _{RLS jest często} określany _jako mezokompleks.

${\ Displaystyle {\ rozpocząć {wyrównane} i {\ rozpocząć {macierz} \ operatorname {M} + \ operatorname {L} _ {R} + \ operatorname {L} _ {S} \ quad \ rightleftharpoons \ quad & \ operatorname {ML} _{R}\mathrm {L} _{R}&+&\mathrm {ML} _{S}\mathrm {L} _{S}&+&\mathrm {ML} _{R}\ mathrm {L} _{S}&\\&x&&y&&z&\left\}\quad {\overset {}{\text{stężenia}}}\right.\\&\\&\left\downarrow {\begin{macierz} \\\mathrm {r} _{RR}\\\\\end{macierz}}\right.&&\left\downarrow {\begin{macierz}\\\mathrm {r} _{SS}\\\\ \end{macierz}}\right.&&\left\strzałka w dół {\begin{matrix}\\\mathrm {r} _{RS}\\\\\end{matrix}}\right.&\left\}\ quad {\overset {}{\text{stawki}}}\right.\qquad \qquad \\\end{macierz}}\\\\&\qquad \qquad \qquad \qquad \qquad \qquad \;\; \;\;\;{\text{produkty reakcji}}\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;\;{\text{ee}}_{ \text{produkt}}\\\\&{\text{stała równowagi: }}K={\frac {z^{2}}{xy}}\end{aligned}}}$

Podstawowy schemat modelu ML ₂ opracowany przez HB Kagana

Stała równowagi , która opisuje tę równowagę, K, jest przypuszczalnie niezależna od katalitycznej reakcji chemicznej. W modelu Kagana K zależy od ilości agregacji obecnej w środowisku chemicznym. AK=4 uważa się za stan, w którym istnieje statystyczny rozkład ligandów do każdego kompleksu metalu. tworzenie heterochiralnych kompleksów przy K=4 nie ma termodynamicznych wad ani zalet.

Przestrzegając tego samego prawa szybkości kinetycznej , każdy z trzech kompleksów katalitycznych katalizuje pożądaną reakcję, tworząc produkt. Jako swoje enancjomery kompleksy homochiralne katalizują reakcję z tą samą szybkością, chociaż indukowana jest przeciwna konfiguracja absolutna produktu (tj. r _RR = r _SS ). Jednakże kompleks heterochiralny tworzy racemiczny przy innej stałej szybkości (tj. rRS ₎ .

modelu ML ₂

Aby opisać model ML ₂ w parametrach ilościowych, Kagan i współpracownicy opisali następujący wzór:

${\ Displaystyle ee _ {\ tekst {produkt}} = ee _ {\ tekst {max}} ee_ {\ tekst {pomocniczy}} (1+\beta )/(1+g\,\beta )}$

We współczynniku korekcyjnym Kagan i współpracownicy wprowadzili dwa nowe parametry nieobecne w równaniu 1, β i g. Na ogół parametry te reprezentują stężenie i aktywność trzech kompleksów katalitycznych względem siebie. β oznacza względną ilość kompleksu heterochiralnego (ML RLS ₎ , jak pokazano w równaniu 3. Należy zauważyć, że stała równowagi K jest niezależna zarówno od β, jak i od g _. Jak opisała Donna Blackmond z Scripps Research Institute , „parametr K jest nieodłączną właściwością mieszaniny katalizatorów, niezależną od ee _katalizator . K jest również niezależny od samej reakcji katalitycznej, a zatem niezależny od parametru g”.

${\ Displaystyle \ beta = z / (x + y)}$

Równanie 3: Współczynnik korygujący β można opisać jako z, stężenie kompleksu heterochiralnego podzielone przez x i y, odpowiednie stężenia stężenia kompleksu podzielone przez x i y, odpowiednie stężenia kompleksów homochiralnych

Parametr g reprezentuje reaktywność kompleksu heterochiralnego w stosunku do kompleksów homochiralnych. Jak pokazano na równaniu 5, można to opisać za pomocą stałych szybkości. Ponieważ kompleksy homochiralne reagują z identycznymi szybkościami, g można następnie opisać jako stałą szybkości odpowiadającą kompleksowi heterochiralnemu podzieloną przez stałą szybkości odpowiadającą któremukolwiek z kompleksów homochiralnych.

${\ Displaystyle g = r_ {rs} / r_ {rr}}$

4 : Parametr korygujący, g, można opisać jako szybkość tworzenia produktu z katalizatorem heterochiralnym ML _{RLS podzieloną przez szybkość} tworzenia produktu kompleksu homochiralnego (ML _R L _R lub ML _SLS ).

Interpretacja wyników matematycznych modelu ML ₂

• Jeżeli β=0 lub g=1, równanie ML2 _upraszcza się do równania 1. Żaden kompleks mezokatalizatora nie jest obecny ani aktywny. Dlatego proste właściwości addytywne powinny mieć zastosowanie do takiego scenariusza, aby ustalić liniową zależność między enancjoselektywnością produktu a enancjoczystością chiralnego katalizatora.

• Jeśli współczynnik korekcji jest większy niż jeden, reakcja wykazuje asymetryczne wzmocnienie , znane również jako dodatni efekt nieliniowy. W ramach ML ₂ model, (+) -NLE wnioskuje o mniej reaktywnym heterochiralnym katalizatorze. W tym przypadku stała równowagi K również wzrasta wraz ze wzrostem współczynnika korygującego. Chociaż enancjoselektywność produktu jest stosunkowo wysoka w porównaniu z enancjoczystością katalizatora chiralnego, odbywa się to kosztem ogólnej szybkości reakcji. Aby uzyskać asymetryczną amplifikację, musi istnieć stosunkowo duże stężenie kompleksu heterochiralnego. Ponadto ten heterochiralny kompleks musi mieć znacznie mniejszą szybkość reaktywności, _rRS . Dlatego reaktywne formy katalityczne powinny zmniejszać stężenie, co prowadzi do ogólnie wolniejszej szybkości reakcji.

• Jeśli współczynnik korekcji jest mniejszy niż jeden, reakcja wykazuje asymetryczne wyczerpanie, znane również jako ujemny efekt nieliniowy. W tym scenariuszu katalizator heterochiralny jest stosunkowo bardziej reaktywny niż kompleksy katalizatora homochiralnego. W tym przypadku (-) -NLE może skutkować ogólnie szybszym, chociaż mniej selektywnym tworzeniem produktu.

iv. Kinetyka reakcji z modelem ML ₂ : Po opublikowaniu przez HB Kagana modelu ML ₂ profesor Donna Blackmond ze Scripps zademonstrowała, w jaki sposób można wykorzystać ten model do obliczenia ogólnych szybkości reakcji. Przy tych względnych szybkościach reakcji Blackmond pokazał, w jaki sposób można wykorzystać model ML _{2 do sformułowania przewidywań kinetycznych, które można następnie porównać z danymi eksperymentalnymi.} Ogólne równanie szybkości, Równanie 6, pokazano poniżej.

${\ Displaystyle R = (x + y + gz) r_ {RR}}$

Oprócz dobrego dopasowania do modelu, informacje kinetyczne dotyczące całej reakcji mogą dodatkowo potwierdzić proponowany mechanizm reakcji. Na przykład dodatni NLE w ML ₂ powinien skutkować ogólnie niższą szybkością reakcji. Rozwiązując szybkość reakcji z równania 6, można potwierdzić, czy tak jest.

Model M*L ₂

Ogólny opis

Podobnie jak w modelu ML ₂ , ten zmodyfikowany system obejmuje chiralne ligandy wiążące się z metalowym centrum (M), tworząc nowe centrum chiralności. W modelu M* _L2 występują cztery pary enancjomerycznych kompleksów chiralnych , jak pokazano na rycinie 5.

${\ Displaystyle {\ rozpocząć {macierz} {\ rozpocząć {macierz} \ operatorname {M} + \ operatorname {L} _ {R} + \ operatorname {L} _ {S} \ quad \ rightleftharpoons \ rightleftharpoons \ quad \\ \\\\\\\\&\end{macierz}}{\begin{wyrównane}&{\begin{macierz}\mathrm {M} _{R}\mathrm {L} _{R}\mathrm {L { L} _{S}\mathrm {L} _{R}&+&\mathrm {M} _{R}\mathrm {L} _{S}\mathrm {L} _{S}\\\mathrm { M} _{S}\operatorka {L} _{S}\operatorka {L} _{S}&+&\operatorka {M} _{S}\operatorka {L} _{S}\operatorka {L} _{R}&+&\operatorka {M} _{S}\operatorka {L} _{R}\operatorka {L} _{S}&+&\operatorka {M} _{S}\operatorka {L } _{R}\mathrm {L} _{R}\\&\\\left\downarrow {\begin{matrix}k_{0}\\\pm EE_{0}\end{macierz}}\right. &&\left\strzałka w dół {\begin{macierz}k_{1}\\\pm EE_{1}\end{macierz}}\right.&&\left\strzałka w dół {\begin{macierz}k_{2}\\\ pm EE_{2}\end{macierz}}\right.&&\left\downarrow {\begin{macierz}k_{3}\\\pm EE_{3}\end{macierz}}\right.\end{macierz }}\\\\&\qquad \qquad \qquad \qquad \qquad \,\,\,\,{\text{produkty}}\end{wyrównane}}\end{macierz}}}$

Rysunek 5: Równowaga obecna w M* _L2 . Jest to bardzo podobne do modelu ML ₂ . Jednak ze względu na nowe centrum chiralności istnieją cztery zestawy enancjomerów.

W tym modelu można dokonać przybliżenia, że ​​kompleksy dimeryczne dysocjują nieodwracalnie do form monomerycznych . W tym przypadku do modelu ML* _{2 mają zastosowanie te same równania matematyczne} , co do modelu ML ₂ .

Model ML3 _{_}

Ogólny opis

Wyższy poziom modelowania, model ML ₃ obejmuje cztery aktywne kompleksy katalityczne: ML _R L _R L _R , ML _S L _S L _S , ML _R L _R L _S , ML _S L _S L _R . W przeciwieństwie _do ML2 model, w którym tylko dwa homochiralne kompleksy reagowały, tworząc enancjomerycznie wzbogacony produkt, wszystkie cztery kompleksy katalityczne reagują enancjoselektywnie. Jednak to samo założenie stanu ustalonego dotyczy równowagi między niezwiązanymi i związanymi kompleksami katalitycznymi, jak w prostszym modelu ML ₂ . Zależność tę pokazano poniżej na rysunku 7.

${\ Displaystyle {\ ce {{M} + {L_ {R}} + L_ {S}<=>}} \ \ underbrace {\ ce {ML_ {R} L_ {R} L_ {R}}} _ { x}+\underbrace {\ce {ML_{S}L_{S}L_{S}}} _{y}+\underbrace {\ce {ML_{R}L_{R}L_{S}}} _{ z}+\underbrace {\ce {ML_{S}L_{S}L_{R}}} _{w}}$

Rycina 7: Równowaga między niezwiązanymi formami i reaktywnymi formami katalitycznymi w modelu ML ₃ .

Modelowanie matematyczne

_iloczynu ee jest znacznie trudniejsze niż w prostym modelu ML ₂ . Każdy z dwóch heterochiralnych kompleksów katalitycznych powinien reagować z tą samą szybkością. Homochiralne kompleksy katalityczne, podobnie jak w przypadku ML ₂ , również powinny reagować z tą samą szybkością. W związku z tym parametr korekcji g jest nadal obliczany jako szybkość heterochiralnego kompleksu katalitycznego podzielona przez szybkość homochiralnego kompleksu katalitycznego. Ponieważ jednak kompleksy heterochiralne prowadzą do produktu wzbogaconego enancjomerycznie, ogólne równanie do obliczania produktu _ee staje się trudniejsze. Na rysunku 8 przedstawiono wzór matematyczny do obliczania enancjoselektywności.

${\ Displaystyle EE _ {\ tekst {prod}} = EE_ {0} ee _ {\ tekst {aux}} {\ Frac {3 + 3 \, g \, EE'_ {0}/EE_ {0} + (1 -3\,g\,EE'_{0}/EE_{0})ee_{\text{aux}}^{2}}{1+3\,g+3(1-g)ee_{\text {pomocniczy}}^{2}}}}$

Rysunek 8: Wzór matematyczny opisujący system ML ₃ . _Produkt ee jest obliczany przez pomnożenie ee _max przez współczynnik korygujący opracowany przez Kagana i współpracowników.

Interpretacja modelu ML ₃

Ogólnie rzecz biorąc, interpretacja wartości parametru korekcji g w celu przewidzenia pozytywnych i negatywnych efektów nieliniowych jest znacznie trudniejsza. W przypadku, gdy kompleksy heterochiralne ML _R L _R L _S i ML _S L _S L _R są mniej reaktywne niż kompleksy homochiralne ML _S L _S L _S i ML _R L _R L _R , zachowanie kinetyczne podobne do ML ₂ obserwowany jest model (Rysunek 9). Jednak zasadniczo odmienne zachowanie obserwuje się w przypadku, gdy kompleksy heterochiralne są bardziej reaktywne niż kompleksy homochiralne.

Rycina 9: Gdy kompleksy heterochiralne są bardziej selektywne i reaktywne niż kompleksy homochiralne.

Rycina 10: Kiedy kompleksy homochiralne są bardziej selektywne i reaktywne niż kompleksy heterochiralne.

Efekt zbiornika

Ogólny opis

Często opisywany obok lub we współpracy z modelem ML ₂ , efekt rezerwuarowy opisuje scenariusz, w którym część chiralnego ligandu jest przydzielana do puli nieaktywnych heterochiralnych kompleksów katalitycznych poza cyklem katalitycznym. Pula niereaktywnych katalizatorów heterochiralnych, opisana pulą ee _, rozwija równowagę z aktywnymi katalitycznie kompleksami homochiralnymi, opisana za pomocą ee _efektywnej . W zależności od stężenia nieaktywnej puli katalizatorów można obliczyć czystość enancjomeryczną aktywnych kompleksów katalizatorów. Ogólnym wynikiem efektu rezerwuarowego jest a amplifikacja asymetryczna, znana również jako (+)-NLE.

Pochodzenie efektu zbiornika

Pula niereaktywnych kompleksów katalitycznych, opisana w efekcie rezerwuarowym, może być wynikiem kilku czynników. Jednym z nich może być potencjalnie efekt agregacji heterochiralnych kompleksów katalitycznych, który ma miejsce przed osiągnięciem równowagi w stanie ustalonym.

Wczesne przykłady efektu nieliniowego

Sharpless epoksydowanie geraniolu

W 1986 Kagan i współpracownicy byli w stanie zademonstrować NLE z epoksydacją Sharplessa (E)-geraniolu (ryc. 11). W warunkach utleniających Sharplessa z Ti (Oi-Pr) ₄ / (+) -DET / t-BuOOH, Kagan i współpracownicy byli w stanie wykazać, że istnieje nieliniowa korelacja między produktem ee _a ee chiralnego katalizatora, winian dietylu (DET). Jak widać na rycinie 11, zaobserwowano większy _{iloczyn ee niż oczekiwano.} Zgodnie z modelem ML ₂ , Kagan i współpracownicy byli w stanie stwierdzić, że obecny był mniej reaktywny heterochiralny kompleks DET. Wyjaśniałoby to zatem obserwowaną asymetryczną amplifikację. Dane NLE są również zgodne z mechanizmem asymetrycznej epoksydacji Sharplessa.

Rysunek 11: Ogólny schemat reakcji przebadany przez Kagana i współpracowników dla epoksydacji Sharplessa geraniolu.

Asymetryczne utlenianie siarczków

W 1994 Kagan i współpracownicy opisali NLE w asymetrycznym utlenianiu siarczków. Dobroć dopasowania danych reakcji odpowiadała modelowi ML ₄ . Sugerowało to, że dimeryczny tytan w kompleksie z 4 ligandami DET był aktywnym ugrupowaniem katalitycznym. W takim przypadku szybkość reakcji byłaby znacznie większa w stosunku do idealnej kinetyki reakcji. Upadek, podobnie jak we wszystkich scenariuszach (-) -NLE, polega na tym, że enancjoselektywność była niższa niż oczekiwano. Poniżej, na rysunku 12, widać, że wklęsłość punktów danych jest wysoce wskazująca na (-) -NLE.

Figura 12: Wyraźne wskazanie negatywnego efektu nieliniowego w asymetrycznej reakcji utleniania siarczku.

Kataliza prebiotyczna i efekt nieliniowy

chemii prebiotycznej układy autokatalityczne odgrywają znaczącą rolę w zrozumieniu pochodzenia chiralności w życiu . Reakcja autokatalityczna, reakcja, w której produkt działa jako katalizator dla siebie, służy jako model homochiralności . Asymetryczna reakcja Soai jest powszechnie określana jako chemiczne prawdopodobieństwo tej hipotezy prebiotycznej. W układzie tym obserwuje się asymetryczną amplifikację podczas procesu katalizy autokatalitycznej. Profesor Donna Blackmond intensywnie badała NLE tej reakcji, używając ML _{2 Kagana} Model. Na podstawie tej analizy matematycznej Blackmond był w stanie wywnioskować, że dimeryczny, homochiralny kompleks był aktywnym katalizatorem promującym homochiralność reakcji Soai.