Faktoryzacja koła

Faktoryzacja koła z n=2x3x5=30. W żółtych obszarach nie pojawią się liczby pierwsze.

Faktoryzacja koła jest ulepszeniem metody dzielenia próbnego dla faktoryzacji liczb całkowitych .

Metoda dzielenia próbnego polega na dzieleniu kolejno liczby, która ma być rozłożona na czynniki, przez pierwsze liczby całkowite (2, 3, 4, 5, ...) aż do znalezienia dzielnika. W przypadku rozkładu na czynniki koła zaczyna się od małej listy liczb, zwanej podstawą — zwykle kilku pierwszych liczb pierwszych ; następnie generuje się listę, zwaną kołem , liczb całkowitych, które są względnie pierwsze ze wszystkimi liczbami podstawy. Następnie, aby znaleźć najmniejszy dzielnik liczby do rozłożenia na czynniki, dzieli się ją kolejno przez liczby w podstawie iw kole.

Przy podstawie {2, 3} metoda ta redukuje liczbę podziałów do 1/3 < 34% liczby potrzebnej do próbnego podziału. Większe podstawy jeszcze bardziej zmniejszają tę proporcję; na przykład z podstawą {2, 3, 5} do 8/30 < 27% ; iz podstawą {2, 3, 5, 7} do 48/210 < 23% .

Typowy przykład

Przy danej podstawie kilku pierwszych liczb pierwszych {2, 3, 5} „pierwszy obrót” koła składa się z:

7, 11, 13, 17, 19, 23, 29, 31 .

Drugi obrót uzyskuje się przez dodanie 30, iloczynu podstawy, do liczb w pierwszym turze. Trzecią turę uzyskuje się, dodając 30 do drugiej tury i tak dalej.

Dla realizacji metody można zauważyć, że przyrosty między dwoma kolejnymi elementami koła, tj

inc = [4, 2, 4, 2, 4, 6, 2, 6],

pozostają takie same po każdej turze.

Sugerowana poniżej implementacja wykorzystuje funkcję pomocniczą div( n , k ), która sprawdza, czy n jest podzielne przez k , i zwraca w tym przypadku wartość true , w przeciwnym razie fałsz . W tej implementacji liczbą do rozłożenia na czynniki jest n , a program zwraca najmniejszy dzielnik n – zwracając samo n , jeśli jest liczbą pierwszą.

     
    
     jeśli  div(  n  , 2) = prawda  to  zwróć  2  jeśli  div(  n  , 3) ​​= prawda  to  zwróć  3  jeśli  div(  n  , 5) = prawda  to  zwróć  5  k  := 7;  i  := 0  podczas gdy  k  *  k  ≤  n  zrób  jeśli  div(  n  ,  k  ) = prawda,  to  zwróć  k  k  :=  k      + inc[  i  ]  jeśli  i  < 7  to  i  :=  i  + 1  jeszcze  i  := 0  powrót  n 

Aby uzyskać pełne rozłożenie liczby całkowitej na czynniki, obliczenia można kontynuować bez ponownego uruchamiania koła na początku. Prowadzi to do następującego programu pełnego rozkładu na czynniki, w którym funkcja „add” dodaje swój pierwszy argument na końcu drugiego argumentu, który musi być listą.

  czynniki := [ ]  while  div(  n  , 2) = prawda  do  czynniki := add(2, czynniki)  n  :=  n  / 2  while  div(  n  , 3) ​​= prawda  do  czynniki := add(3, czynniki)  n  :=  n  / 3  podczas gdy  div(  n  , 5) = prawda  do  czynniki := add(5, czynniki)  n  :=  n  / 5  k  := 7;  i  := 0  natomiast  k  
    
    
             *  k  ≤  n  do  if  div(  n  ,  k  ) = true  then  add(  k  , factors)  n  :=  n  /  k  else  k  :=  k  + inc[  i  ]  if  i  < 7  to  i  :=  i  + 1  else  i  := 0  jeśli  n  > 1  to  dodaj(  n  , czynniki)  współczynniki  zwrotu 

Kolejna prezentacja

Faktoryzacja koła służy do generowania list składających się głównie z liczb pierwszych na podstawie prostego wzoru matematycznego i znacznie mniejszej listy pierwszych liczb pierwszych. Listy te można następnie wykorzystać w próbnym podziale lub sitach . Ponieważ nie wszystkie liczby na tych listach są liczbami pierwszymi, wprowadza to nieefektywne operacje redundantne. Jednak same generatory wymagają bardzo mało pamięci w porównaniu do przechowywania czystej listy liczb pierwszych. Mała lista początkowych liczb pierwszych stanowi kompletne parametry algorytmu do generowania pozostałej części listy. Te generatory to tzw koła . Chociaż każde koło może generować nieskończoną listę liczb, po przekroczeniu pewnego punktu liczby przestają być w większości liczbami pierwszymi.

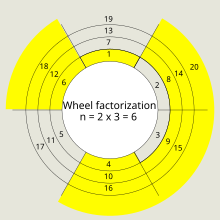
Sposób można ponadto stosować rekurencyjnie jako sito z kołem liczb pierwszych w celu generowania dokładniejszych kół. Paul Pritchard wykonał wiele ostatecznych prac nad faktoryzacją kół, sitami wykorzystującymi faktoryzację kół i sitami kołowymi, formułując szereg różnych algorytmów. Aby zwizualizować użycie koła faktoryzacji, można zacząć od zapisania liczb naturalnych wokół okręgów, jak pokazano na sąsiednim diagramie. Liczba szprych jest tak dobrana, że ​​liczby pierwsze będą miały tendencję do gromadzenia się w mniejszości szprych.

Przykładowa procedura graficzna

1. Znajdź kilka pierwszych liczb pierwszych, aby utworzyć podstawę koła faktoryzacji. Są one znane lub być może określone na podstawie wcześniejszych zastosowań mniejszych kół faktoryzacji lub szybkiego ich znalezienia za pomocą Sita Eratostenesa .
2. Pomnóż przez siebie podstawowe liczby pierwsze, aby otrzymać wynik n , który jest obwodem koła faktoryzacji.
3. Wpisz liczby od 1 do n w kółko. Będzie to najbardziej wewnętrzne koło reprezentujące jeden obrót koła.
4. Od liczb od 1 do n w najbardziej wewnętrznym okręgu wykreśl wszystkie wielokrotności podstawowych liczb pierwszych z kroku pierwszego, tak jak zastosowano w kroku 2. Tę eliminację liczby złożonej można przeprowadzić albo za pomocą sita, takiego jak sito Eratostenesa, albo jako wynikiem zastosowania mniejszych kół faktoryzacji.
5. Biorąc x za liczbę okręgów zapisanych do tej pory, kontynuuj pisanie xn + 1 do xn + n w koncentrycznych okręgach wokół najbardziej wewnętrznego okręgu, tak aby xn + 1 znajdowało się w tej samej pozycji co ( x − 1) n + 1.
6. Powtarzaj krok 5, aż największy okrąg obrotu obejmie największą liczbę, która ma być testowana pod kątem pierwszorzędności.
7. Skreśl cyfrę 1.
8. Odetnij szprychy liczb pierwszych, jak w kroku 1 i zastosowano w kroku 2, we wszystkich zewnętrznych okręgach bez wykreślania liczb pierwszych w najbardziej wewnętrznym okręgu (w kole 1).
9. Wykreśl szprychy wszystkich wielokrotności liczb pierwszych wykreślonych z wewnętrznego koła 1 w kroku 4 w taki sam sposób, jak wykreślono szprychy podstawowych liczb pierwszych w kroku 8.
10. Pozostałe liczby w kole to w większości liczby pierwsze (zbiorczo nazywane są „względnie” pierwszymi). Użyj innych metod, takich jak Sito Eratostenesa lub dalsze zastosowanie większych kół faktoryzacji, aby usunąć pozostałe liczby niebędące liczbami pierwszymi.

Przykład

Faktoryzacja koła z n=2x3=6

1. Znajdź 2 pierwsze liczby pierwsze: 2 i 3.

2. n = 2 × 3 = 6

3.

1 2 3 4 5 6

4. skreślić czynniki 2 i 3, które wynoszą 4 i 6 jako czynniki 2; 6 jako jedyny czynnik 3 jest już uderzony:

 1 2 3  4  5  6 

5. x = 1. xn + 1 = 1 · 6 + 1 = 7. ( x + 1) n = (1 + 1) · 6 = 12. Zapisz od 7 do 12, gdzie 7 jest wyrównane z 1.

 1 2 3  4 5  6  7  8 9 10 11 12 

6. x = 2. xn + 1 = 2 · 6 + 1 = 13. ( x + 1) n = (2 + 1) · 6 = 18. Zapisz od 13 do 18. Powtórz dla kilku następnych wierszy.

 1 2 3  4 5  6  7  8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 

7 i 8. Przesiewanie

       1  2 3  4 5  6  7  8  9  10  11 12 13  14  15  16 17 18  19  20 21  22 23 24 25 26 27  28  29  30 

9. Przesiewanie

           1  2 3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30 

10. Otrzymana lista zawiera liczbę inną niż pierwsza 25, czyli 5 ² . Użyj innych metod, takich jak sito, aby go wyeliminować

2 3 5 7 11 13 17 19 23 29

Zauważ, że używając dokładnie następnej liczby pierwszej z 5 cykli koła i eliminując wielokrotności tej liczby pierwszej (i tylko tej liczby pierwszej) z wynikowej listy, otrzymaliśmy koło podstawowe zgodnie z krokiem 4 dla koła faktoryzacji z podstawą liczby pierwsze 2, 3 i 5; jest to jedno koło przed poprzednim kołem faktoryzacji 2/3. Można następnie wykonać kroki do kroku 10, używając następnej kolejnej liczby pierwszej 7 cykli i usuwając tylko wielokrotności 7 z wynikowej listy w kroku 10 (pozostawiając niektóre „względne” liczby pierwsze w tym przypadku i we wszystkich kolejnych przypadkach - tj. niektóre nieprawdziwe w pełni kwalifikowane liczby pierwsze), aby uzyskać następne, bardziej zaawansowane koło, rekurencyjnie powtarzając kroki w razie potrzeby, aby uzyskać kolejno większe koła.

Analiza i implementacja komputerowa

Formalnie metoda wykorzystuje następujące spostrzeżenia: Po pierwsze, zbiór podstawowych liczb pierwszych połączony z jego (nieskończonym) zbiorem liczb względnie pierwszych jest nadzbiorem liczb pierwszych. Po drugie, że nieskończony zbiór liczb względnie pierwszych można łatwo wyliczyć od liczb względnie pierwszych do zbioru podstawowego między 2 a iloczynem zbioru podstawowego. (Zauważ, że 1 wymaga specjalnej obsługi.)

Jak widać na powyższym przykładzie, wynikiem wielokrotnych zastosowań powyższej procedury rekurencyjnej od kroków 4 do 10 może być lista kół obejmująca dowolny pożądany zakres przesiewania (do którego można ją skrócić), a wynikowa lista zawiera wtedy tylko wielokrotności liczb pierwszych wyższych niż jedna po ostatnio użytych podstawowych liczbach pierwszych.

Zauważ, że gdy koło osiągnie pożądaną górną granicę zakresu przesiewania, można zatrzymać generowanie kolejnych kół i wykorzystać informacje w tym kole do wybrania pozostałych liczb złożonych z tej ostatniej listy kół za pomocą techniki typu Sito Eratostenesa, ale wykorzystując lukę wzór charakterystyczny dla koła, aby uniknąć zbędnych ubojów; niektóre optymalizacje mogą być możliwe w oparciu o fakt (zostanie udowodniony w następnej sekcji), że nie będzie powtórnego usuwania dowolnej liczby złożonej: każdy pozostały złożony zostanie usunięty dokładnie raz. Alternatywnie, można nadal generować skrócone listy kół, używając liczb pierwszych aż do pierwiastka kwadratowego z żądanego zakresu sita, w którym to przypadku wszystkie pozostałe reprezentacje liczb w kole będą liczbami pierwszymi; jednakże, chociaż ta metoda jest tak wydajna, że ​​nigdy nie usuwa liczb złożonych więcej niż jeden raz, traci dużo czasu poza zwykle rozważanymi operacjami usuwania podczas przetwarzania kolejnych przebiegów koła, tak że trwa znacznie dłużej. Eliminacja liczb złożonych za pomocą koła faktoryzacyjnego opiera się na następującej zasadzie: Mając liczbę k > n, wiemy, że k nie jest liczbą pierwszą, jeśli k mod n i n nie są względnie pierwsze. Na tej podstawie można określić ułamek liczb, który eliminuje sito koła (chociaż nie wszystkie muszą być fizycznie odkreślone; wiele można usunąć automatycznie w operacjach kopiowania mniejszych kół do większych kół) jako 1 - phi (n)/n, czyli również wydajność sita.

Wiadomo, że

${\ Displaystyle \ lim \ inf {\ Frac {\ varphi (n)} {n}} \ log \ log n = e ^ {- \gamma}\sim 0,56145948,}$

gdzie γ jest stałą Eulera . Zatem phi(n) / n dąży do zera powoli, gdy n rośnie do nieskończoności i widać, że ta wydajność rośnie bardzo powoli do 100% dla nieskończenie dużego n. Z własności phi można łatwo zauważyć, że najbardziej wydajne sito mniejsze od x to takie, w którym ${\ Displaystyle n = p_ {1} p_ {2} ... p_ {i}<x}$ i ${\ Displaystyle np_ {i + 1} \ geq x}$ (tj. generowanie koła może się zatrzymać, gdy ostatnie koło przejdzie lub ma wystarczający obwód, aby objąć najwyższą liczbę w zakresie przesiewania).

Aby maksymalnie wykorzystać komputer, chcemy, aby liczby, które są mniejsze niż n i względnie pierwsze, były zbiorem. Korzystając z kilku obserwacji, zestaw można łatwo wygenerować:

1. Zacznij od $2$ jest zbiorem dla $n = 1}$ pierwszą liczbą pierwszą Ten zestaw początkowy oznacza, że ​​wszystkie liczby zaczynające się od dwóch w górę są uwzględniane jako „względne” liczby pierwsze, ponieważ obwód koła wynosi 1.
2. Następujące zestawy to ${\ Displaystyle S_ {2} = \ {1 \}},$ co oznacza, że ​​zaczyna się od 3 dla wszystkich liczb nieparzystych z wyeliminowanymi czynnikami 2 (obwód 2), $wyeliminowane współczynniki 2 i 3$ jak w przypadku początkowego koła podstawowego w powyższym przykładzie i tak dalej
3. Niech ${n}$$S_$ k { .
4. Wtedy ${\ Displaystyle S_ {np_ {i + 1}} = F_ {p_ {i + 1}} [S_ {n} \ kubek S_ {n} + n \ kubek S_ {n} + 2n \ kubek ... \ kubek S_ {n} + n (p_ {i + 1} -1)]}$ gdzie reprezentuje operację usuwania wszystkich wielokrotności x. ${\ displaystyle F_ {x}}$
5. 1 i ${\ Displaystyle p_ {i + 1}}$ będą dwoma najmniejszymi z n $\ Displaystyle n> 2$$}$ usuwając potrzebę obliczania liczb pierwszych oddzielnie, chociaż algorytm musi prowadzić rejestr wszystkich wyeliminowanych podstawowych liczb pierwszych, które nie są już zawarte w kolejnych zestawach.
6. Wszystkie zestawy, w których obwód n > 2 są symetryczne wokół ${\ displaystyle n/2}$ , zmniejszając wymagania dotyczące przechowywania. Poniższy algorytm nie wykorzystuje tego faktu, ale opiera się na fakcie, że odstępy między kolejnymi liczbami w każdym zestawie są symetryczne wokół połowy.

Zobacz też

• Sito Sundarama
• Sito Atkina
• Teoria sita

Linki zewnętrzne

• Faktoryzacja koła
• Ulepszone przyrostowe sita liczb pierwszych autorstwa Paula Pritcharda