Gatunki kombinatoryczne

W matematyce kombinatorycznej teoria gatunków kombinatorycznych jest abstrakcyjną, systematyczną metodą wyprowadzania funkcji generujących struktur dyskretnych, która pozwala nie tylko policzyć te struktury, ale także dać bijektywne dowody z ich udziałem. Przykładami gatunków kombinatorycznych są ( skończone ) grafy , permutacje , drzewa i tak dalej; każdy z nich ma powiązaną funkcję generującą, która zlicza, ile jest struktur o określonym rozmiarze. Jednym z celów teorii gatunków jest możliwość analizowania skomplikowanych struktur poprzez opisywanie ich w kategoriach przekształceń i kombinacji prostszych struktur. Operacje te odpowiadają równoważnym manipulacjom funkcji generujących, więc tworzenie takich funkcji dla skomplikowanych struktur jest znacznie łatwiejsze niż innymi metodami. Teoria została wprowadzona, starannie opracowana i zastosowana przez kanadyjską grupę ludzi skupionych wokół André Joyala .

Siła teorii wynika z jej poziomu abstrakcji. „Format opisu” struktury (taki jak lista sąsiedztwa a macierz sąsiedztwa dla grafów) nie ma znaczenia, ponieważ gatunki są czysto algebraiczne. Teoria kategorii zapewnia użyteczny język dla pojawiających się tutaj pojęć, ale nie jest konieczne zrozumienie kategorii, aby móc pracować z gatunkami.

Kategoria gatunków jest równoważna kategorii sekwencji symetrycznych w zbiorach skończonych.

Definicja gatunku

Schematyczna ilustracja kombinatorycznej struktury gatunków na pięciu elementach za pomocą diagramu Labelle

Każda struktura — instancja określonego gatunku — jest powiązana z pewnym zbiorem , a często istnieje wiele możliwych struktur dla tego samego zbioru. Na przykład możliwe jest skonstruowanie kilku różnych grafów, których etykiety węzłów pochodzą z tego samego zbioru. Jednocześnie do budowy konstrukcji można było użyć dowolnego zestawu. Różnica między jednym gatunkiem a drugim polega na tym, że budują inny zestaw struktur z tego samego zestawu podstawowego.

Prowadzi to do formalnej definicji gatunku kombinatorycznego . Niech będzie kategorią $zbiorów$ skończonych , przy czym morfizmami kategorii będą bijekcje między tymi . Gatunek jest funktorem _

{\ Displaystyle F \ dwukropek {\ mathcal {B}} \ do {\ mathcal {B}}.}

Dla każdego skończonego zbioru A w , skończony zbiór F [ $ZA$ ] nazywany jest zbiorem struktur F na lub zbiorem struktur gatunków F na A . Ponadto, zgodnie z definicją funktora, jeśli φ jest bijekcją między zbiorami A i B , to F [φ] jest bijekcją między zbiorami F -struktur F [ A ] i F [ B ], zwaną transportem F- struktury wzdłuż φ .

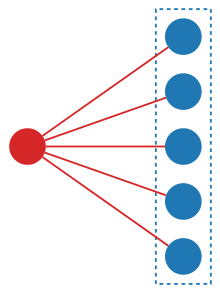
Na przykład „gatunek permutacji” odwzorowuje każdy skończony zbiór A na zbiór wszystkich permutacji A , a każda bijekcja od A do innego zbioru B naturalnie indukuje bijekcję ze zbioru wszystkich permutacji A do zbioru wszystkich permutacji z B. _ Podobnie „rodzaje przegród” można zdefiniować, przypisując każdemu skończonemu zbiorowi zbiór wszystkich jego przegród , a „gatunki zbioru potęgowego” przypisuje każdemu skończonemu zbiorowi jego zbiór potęgowy . Diagram obok przedstawia konstrukcję na zestawie pięciu elementów: łuki łączą konstrukcję (kolor czerwony) z elementami (kolor niebieski), z których jest zbudowana.

mają tę samą liczność (liczbę elementów), dla każdego skończonego zbioru ZA , liczność , czyli ${\ Displaystyle F [A]}$ skończony, zależy tylko od liczności A . (Wynika to z formalnej definicji funktora). W szczególności można zdefiniować wykładniczy szereg generujący F ( x ) gatunku F :

{\ Displaystyle F (x) = \ suma _ {n \ geq 0} \ nazwa operatora {Karta} F [n] {\ Frac {x ^ {n}} {n!}}}

gdzie $_$ licznością $_$ _ _ _ _ _ np. ${\ Displaystyle A = \ {1,2, \ kropki, n \}}$ .

Kilka przykładów: pisanie ${\ Displaystyle f_ {n} = \ operatorname {karta} F [n]$ }

Gatunkiem zbiorów (tradycyjnie nazywanym E , od francuskiego „ zespołu ”, co oznacza „zbiór”) jest funktor, który odwzorowuje A na { A }. Wtedy ${\ Displaystyle f_ {n} = 1}$ , więc ${\ Displaystyle E (x) = e ^ {x}}$ .
${\ displaystyle f_ {n} = n!$ powyżej gatunek S permutacji ma f } ${\ Displaystyle S (x) = 1 / (1-x)}$ .
Gatunek T ₂ par (2- krotki ) jest funktorem przenoszącym zbiór A do A ² . wtedy ${\ Displaystyle f_ {n} = n ^ {2}}$ i ${\ Displaystyle T_ {2} (x) = x (x + 1)e^{x}}$ .

Rachunek gatunków

Arytmetyka funkcji generujących odpowiada pewnym „naturalnym” operacjom na gatunkach. Podstawowe operacje to dodawanie, mnożenie, składanie i różniczkowanie; konieczne jest również zdefiniowanie równości gatunków. Teoria kategorii ma już sposób na opisanie, kiedy dwa funktory są równoważne: izomorfizm naturalny . W tym kontekście oznacza to po prostu, że dla każdego A istnieje bijekcja między strukturami F na A i strukturami G na A , która jest „dobrze wychowana” w interakcji z transportem. Gatunki o tej samej funkcji generowania mogą nie być izomorficzne, ale gatunki izomorficzne zawsze mają tę samą funkcję generowania.

Dodatek

Dodawanie gatunków jest definiowane przez rozłączne połączenie zbiorów i odpowiada wyborowi między strukturami. Dla gatunków F i G zdefiniuj ( F + G )[ A ] jako rozłączny związek (również zapisywany jako „+”) F [ A ] i G [ A ]. Wynika z tego, że ( fa + sol )( x ) = fa ( x ) + sol ( x ). Dla demonstracji przyjmijmy, że E ⁺ jest gatunkiem zbiorów niepustych, których funkcją generującą jest E ⁺ ( x ) = e ^x − 1, a 1 gatunkiem zbioru pustego , którego funkcją generującą jest 1 ( x ) = 1. Wynika z tego, że E = 1 + E ⁺ : słownie „zbiór jest albo pusty, albo niepusty”. Równania takie jak to można odczytywać jako odnoszące się do pojedynczej struktury, jak również do całego zbioru struktur.

Mnożenie

Mnożenie gatunków jest nieco bardziej skomplikowane. Możliwe jest po prostu przyjęcie kartezjańskiego iloczynu zbiorów jako definicji, ale kombinatoryczna interpretacja tego nie jest całkiem poprawna. (Zobacz poniżej zastosowanie tego rodzaju iloczynu.) Zamiast łączyć ze sobą dwie niepowiązane struktury w tym samym zbiorze, operator mnożenia wykorzystuje pomysł podzielenia zbioru na dwa składowe, konstruując strukturę F na jednym i G - struktura z drugiej.

{\ Displaystyle (F \ cdot G) [A] = \ suma _ {A = B + C} F [B] \ razy G [C].}

Jest to suma rozłączna na wszystkich możliwych partycjach binarnych A . Łatwo jest pokazać, że mnożenie jest asocjacyjne i przemienne ( aż do izomorfizmu ) oraz rozdzielcze względem dodawania. Jeśli chodzi o szereg generujący, ( F · G )( x ) = F ( x ) G ( x ).

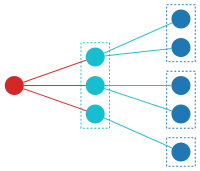
Poniższy diagram przedstawia jedną możliwą ( F · G )-strukturę na zbiorze z pięcioma elementami. Struktura F (czerwona) zawiera trzy elementy zestawu podstawowego, a struktura G (jasnoniebieska) resztę. Inne struktury będą miały F i G dzielące zestaw w inny sposób. Zbiór ( F · G )[ A ], gdzie A jest zbiorem podstawowym, jest sumą rozłączną wszystkich takich struktur.

Dodawanie i mnożenie gatunków jest najbardziej wszechstronnym wyrazem reguł liczenia sum i iloczynów.

Kompozycja

Skład , zwany także substytucją, jest znowu bardziej skomplikowany. Podstawową ideą jest zamiana składowych F na struktury G , tworzące ( F ∘ G ). Podobnie jak w przypadku mnożenia, odbywa się to poprzez podzielenie zbioru wejściowego A ; rozłączne podzbiory są przekazywane do G , aby utworzyć G -struktury, a zbiór podzbiorów jest przekazywany do F , aby utworzyć F -strukturę łączącą G -struktury. Wymagane jest, aby G mapował pusty zestaw na siebie, aby kompozycja działała. Formalna definicja to:

{\ Displaystyle (F \ circ G) [A] = \ suma _ {\ pi \ w P [A]} (F [\ pi] \ razy \ prod _ {B \ in \ pi} G [B]). }

Tutaj P jest rodzajem partycji, więc P [ A ] jest zbiorem wszystkich partycji A . Ta definicja mówi, że element ( F ∘ G ) [ A ] składa się ze struktury F na pewnym podziale A i struktury G na każdym komponencie podziału. Seria generująca to ${\ Displaystyle (F \ circ G) (x) = F (G (x))}$ .

Poniżej pokazano jedną z takich struktur. Trzy G (jasnoniebieskie) dzielą między siebie pięcioelementowy zestaw podstawowy; następnie F (czerwona) w celu połączenia struktur G.

Te dwie ostatnie operacje można zilustrować na przykładzie drzew. Najpierw zdefiniuj X jako gatunek „singleton”, którego seria generująca to X ( x ) = x . Wtedy gatunek Ar ukorzenionych drzew (od francuskiego „ arborescence ”) jest definiowany rekurencyjnie przez Ar = X · E ( Ar ). To równanie mówi, że drzewo składa się z pojedynczego korzenia i zestawu (pod-)drzew. Rekurencja nie wymaga wyraźnego przypadku podstawowego: generuje drzewa tylko w kontekście zastosowania do pewnego skończonego zbioru. Jednym ze sposobów myślenia o tym jest to, że Ar jest wielokrotnie stosowany do „dostawy” elementów ze zbioru — za każdym razem jeden element jest pobierany przez X , a pozostałe rozdzielane przez E między poddrzewa Ar , dopóki nie zostaną nie ma więcej elementów do nadania E . Pokazuje to, że algebraiczne opisy gatunków różnią się znacznie od specyfikacji typów w językach programowania, takich jak Haskell .

Podobnie gatunek P można scharakteryzować jako P = E ( E ⁺ ): „podział to parami rozłączny zbiór niepustych zbiorów (wykorzystujący wszystkie elementy zbioru wejściowego)”. Wykładniczy szereg generujący dla P to szereg liczb Bella ${\ Displaystyle P (x) = e ^ {(e ^ {x} -1)}}$ .

Różnicowanie

Zróżnicowanie gatunkowe intuicyjnie odpowiada budowaniu „konstrukcji z dziurą”, jak pokazano na poniższej ilustracji.

Formalnie,

{\ Displaystyle (F ') [A] = F [A \ uplus \ {\ gwiazda \}]}

gdzie jest jakiś wyróżniający się nowy element, którego nie ma w $A}$ $displaystyle$ .

Aby odróżnić skojarzony szereg wykładniczy, należy przesunąć ciąg współczynników o jedno miejsce w „lewo” (tracąc pierwszy wyraz). Sugeruje to definicję gatunku: F' [ A ] = F [ A + {*}], gdzie {*} to zbiór singletonowy, a „+” to związek rozłączny. Bardziej zaawansowane części teorii gatunków szeroko wykorzystują zróżnicowanie do konstruowania i rozwiązywania równań różniczkowych dotyczących gatunków i szeregów. Pomysł dodania (lub usunięcia) pojedynczej części struktury jest potężny: można go wykorzystać do ustanowienia relacji między pozornie niezwiązanymi ze sobą gatunkami.

Rozważmy na przykład strukturę gatunku L rzędów liniowych — listy elementów zbioru podstawowego. Usunięcie elementu listy dzieli ją na dwie części (prawdopodobnie pustą); w symbolach jest to L' = L · L . Wykładnicza funkcja generująca L to L ( x ) = 1/(1 - x ) i rzeczywiście:

{\ Displaystyle {\ Frac {d} {dx}} {(1-x)} ^ {-1} = {(1-x)} ^ {-2}.}

Uogólnione wzory różniczkowania można znaleźć we wcześniejszych badaniach NG de Bruijn, opublikowanych w 1964 roku.

Gatunek C permutacji cyklicznych przyjmuje zbiór A do zbioru wszystkich cykli na A . Usunięcie pojedynczego elementu z cyklu redukuje go do listy: C' = L . Możemy zintegrować funkcję generującą L , aby wytworzyć to dla C .

{\ Displaystyle C (x) = \ int _ {0} ^ {x} {\ Frac {dt} {1-t}} = \ log {\ Frac {1} {1-x}}.}

Ładnym przykładem integracji gatunku jest uzupełnienie prostej (skoordynowanej polem) z punktem nieskończonym i otrzymanie prostej rzutowej.

Dalsze operacje

Istnieje wiele innych manipulacji, które można wykonać na gatunkach. Są one niezbędne do wyrażania bardziej skomplikowanych struktur, takich jak grafy skierowane lub bigrafy .

Wskazywanie zaznacza pojedynczy element w strukturze. Biorąc pod uwagę gatunek F , odpowiedni gatunek spiczasty F ^• jest zdefiniowany przez F ^• [ A ] = A × F [ A ]. Zatem każda F ^• -struktura jest F -strukturą z wyróżnionym jednym elementem. Wskazywanie jest związane z różniczkowaniem przez relację F ^• = X · F' , więc F ^• ( x ) = x F' ( x ). Gatunek zbiorów ostro zakończonych , E ^• , jest szczególnie ważny jako budulec wielu bardziej złożonych konstrukcji.

Iloczyn kartezjański dwóch gatunków ^{[ potrzebne źródło ]} to gatunek, który może jednocześnie budować dwie struktury na tym samym zestawie. Różni się od zwykłego operatora mnożenia tym, że wszystkie elementy zbioru podstawowego są wspólne dla obu struktur. ( F × G ) można postrzegać jako superpozycję struktury F i struktury G. Bigrafy można opisać jako superpozycję grafu i zestawu drzew: każdy węzeł bigrafu jest częścią grafu, a jednocześnie częścią jakiegoś drzewa opisującego sposób zagnieżdżania węzłów. Funkcja generująca ( F × G ) ( x ) jest iloczynem Hadamarda lub współczynnikiem F ( x ) i G ( x ).

Gatunek E ^• × E ^• można postrzegać jako dokonujący dwóch niezależnych wyborów ze zbioru podstawowego. Te dwa punkty mogą się pokrywać, inaczej niż w X · X · E , gdzie są zmuszone być różne.

Jako funktory, gatunki F i G można łączyć za pomocą kompozycji funktoralnej : ^{[ potrzebne źródło ]} ${\ Displaystyle (F \, \ Box \, G) [A] =F[G[A]]}$ (symbol kwadratu jest używany, ponieważ kółko jest już używane do podstawienia). Tworzy to F na zbiorze wszystkich struktur G na zbiorze A . Na przykład, jeśli F jest funktorem przyjmującym zbiór do swojego zbioru potęgowego, struktura złożonego gatunku jest pewnym podzbiorem struktur G na A . Jeśli teraz przyjmiemy, G jest E ^• × E ^• z góry, otrzymamy gatunki grafów skierowanych, z dozwolonymi pętlami własnymi. (Graf skierowany jest zbiorem krawędzi, a krawędzie są parami węzłów: więc graf jest podzbiorem zbioru par elementów zbioru węzłów A .) Inne rodziny grafów, jak również wiele innych struktur, mogą określić w ten sposób.

Oprogramowanie

Operacje na gatunkach wspiera SageMath , a przy użyciu specjalnego pakietu również Haskell .

Warianty

Gatunek w k rodzajach to funktor ${\ displaystyle {\ mathcal {B}} ^ {k} \ rightarrow {\ mathcal {B}}}$ . Tutaj produkowane struktury mogą zawierać elementy zaczerpnięte z różnych źródeł. ^{[ potrzebne źródło ]}
Funktor do $szeregu$ R zbiorów dla R pierścienia potęgowego jest gatunkiem ważonym . ^{[ potrzebne źródło ]}

Jeśli „zbiory skończone z bijekcjami” zastąpimy „skończonymi przestrzeniami wektorowymi z przekształceniami liniowymi”, to otrzymamy pojęcie funktora wielomianowego (po nałożeniu warunku skończoności). ^{[ potrzebne źródło ]}

Zobacz też

Kontener (teoria typów)

Notatki

Joyal, André (październik 1981). „Une théorie combinatoire des séries formelles” . Postępy w matematyce . 42 (1): 1–82. doi : 10.1016/0001-8708(81)90052-9 .
Bruijn, de, NG (1964). Teoria liczenia Pólyi. W EF Beckenbach (red.), Stosowana matematyka kombinatoryczna (s. 144-184)
Labelle, Jacques. Quelques espèces sur les zespoły de petite cardinalité. , Ann. Sc. Matematyka Quebec 9.1 (1985): 31-58.
Labelle, J.; Tak, YN (1989). „Związek między pierścieniami Burnside'a a gatunkami kombinatorycznymi” . Dziennik teorii kombinatorycznej . Seria A. 50 (2): 269–284. doi : 10.1016/0097-3165(89)90019-8 .
Yves Chiricota, Classification des espèces moléculaires de degré 6 et 7 , Ann. nauka Matematyka Quebec 17 (1993), no. 1, 1 l–37.
François Bergeron, Gilbert Labelle, Pierre Leroux, Théorie des espèces et combinatoire desstructures arborescentes , LaCIM, Montréal (1994). Wersja angielska: Gatunki kombinatoryczne i struktury podobne do drzew , Cambridge University Press (1998).
Kerber, Adalbert (1999), Zastosowane skończone działania grupowe, algorytmy i kombinatoryka , 19 (wyd. 2), Berlin, Nowy Jork: Springer-Verlag, ISBN 978-3-540-65941-9 , MR 1716962 , OCLC 247593131

Linki zewnętrzne