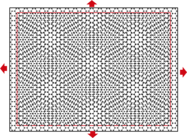
Heterostrain

Termin heterostrain został zaproponowany w 2018 roku w kontekście materiałoznawstwa w celu uproszczenia oznaczania możliwych sytuacji naprężeń w heterostrukturach van der Waalsa, w których dwa (lub więcej) dwuwymiarowe materiały są ułożone jeden na drugim. Warstwy te mogą doświadczać tego samego odkształcenia (homostrain) lub różnych deformacji (heterostrain). Oprócz skrętu , heterostrain może mieć ważne konsekwencje dla właściwości elektronicznych i optycznych powstałej struktury. W związku z tym kontrola heterostrain wyłania się jako poddziedzina szczeptroniki w którym właściwości materiałów 2D są kontrolowane przez odkształcenie.

Etymologia

Heterostrain jest zbudowany z greckiego przedrostka hetero- (inny) i rzeczownika szczep . Oznacza to, że dwie warstwy tworzące strukturę podlegają różnym naprężeniom. Kontrastuje to z homostrain, w którym dwie warstwy podlegają temu samemu naprężeniu. Heterostrain jest określany przez niektórych autorów jako „szczep względny”.

Manifestacja i pomiar heteroszczepu

Dla uproszczenia rozważany jest przypadek dwóch warstw gafenu . Opis można uogólnić na przypadek różnych materiałów 2D tworzących heterostrukturę .

W naturze dwie warstwy grafenu zwykle układają się w stos z przesunięciem o pół komórki elementarnej. Ta konfiguracja jest najbardziej korzystna energetycznie i występuje w graficie . Jeśli jedna warstwa jest naprężona, podczas gdy druga pozostaje nienaruszona, wzór mory sygnalizuje obszary, w których sieci atomowe dwóch warstw są w rejestrze lub poza nim. Kształt wzoru mory zależy od rodzaju szczepu.

  • Jeśli warstwa jest zdeformowana w jednym kierunku (jednoosiowe heteroodkształcenie), efekt mory jest jednowymiarowy.
  • Jeśli warstwa jest naprężona w ten sam sposób w dwóch kierunkach (dwuosiowe heteroodkształcenie), mora jest dwuwymiarową nadbudową.
Bernal stacking
Warstwy grafenu w układaniu Bernala
Biaxial heterostrain
Warstwy grafenu z dwuosiowym heterostrainem
Uniaxial heterostrain
Warstwy grafenu z jednoosiowym heteroodkształceniem

Ogólnie rzecz biorąc, warstwa może zostać zdeformowana przez dowolną kombinację obu typów heteroodkształceń.

Heterostrain można zmierzyć za pomocą skaningowego mikroskopu tunelowego który zapewnia obrazy przedstawiające zarówno sieć atomową pierwszej warstwy, jak i supersieć mory. Odniesienie sieci atomowej do sieci mory pozwala całkowicie określić względny układ warstw (dwuosiowy, jednoosiowy heteroodkształcenie i skręt). Metoda jest odporna na artefakty kalibracji, które w identyczny sposób wpływają na obraz dwóch warstw, co znosi się w pomiarze względnym. Alternatywnie, przy dobrze skalibrowanym mikroskopie i jeśli dwuosiowe heteroodkształcenie jest wystarczająco niskie, możliwe jest określenie skręcenia i jednoosiowego heteroodkształcenia na podstawie znajomości okresu mory we wszystkich kierunkach. Wręcz przeciwnie, znacznie trudniej jest określić homostrain, co wymaga próbki kalibracyjnej.

Geneza i wpływ heterostrain

Heterostrain jest generowany podczas wytwarzania stosu materiałów 2D. Może to wynikać z metastabilnej konfiguracji podczas montażu oddolnego lub z manipulacji warstwami w technice rozdzierania i układania. Wykazano, że jest wszechobecny w skręconych warstwach grafenu w pobliżu magicznego kąta skrętu i jest głównym czynnikiem wpływającym na płaską szerokość pasma tych systemów. Heterostrain ma znacznie większy wpływ na właściwości elektroniczne niż homostrain. Wyjaśnia to część zmienności próbki, która wcześniej była zagadkowa. Badania zmierzają obecnie w kierunku zrozumienia wpływu fluktuacji przestrzennych heterostrain.

  1. ^ a b c d e Huder, Loïc; Artaud, Aleksandr; Le Quang, Toai; de Laissardière, Guy Trambly; Jansen, Alojzy GM; Lapertot, Gerard; Kaplica, Claude; Renard, Vincent T. (2018-04-12). „Elektroniczne widmo skręconych warstw grafenu pod heterostrain” . Listy z przeglądu fizycznego . 120 (15): 156405. arXiv : 1803.03505 . Bibcode : 2018PhRvL.120o6405H . doi : 10.1103/PhysRevLett.120.156405 . PMID    29756887 . S2CID 21734003 .
  2. ^ ab Bi    , Zhen; Yuan, Noe FQ; Fu, Liang (2019-07-31). „Projektowanie płaskich pasm według odkształcenia” . Przegląd fizyczny B. 100 (3): 035448. arXiv : 1902.10146 . Bibcode : 2019PhRvB.100c5448B . doi : 10.1103/PhysRevB.100.035448 . ISSN 2469-9950 . S2CID 118982311 .
  3. ; ^ abc Mesple , Florie   Missaoui, Ahmed; Cea, Tommaso; Huder, Loic; Gwinea, Franciszek; Trambly de Laissardière, Guy; Kaplica, Claude; Renard, Vincent T. (2021-09-17). „Heterostrain określa płaskie pasma w warstwach grafenu skręconych pod kątem magicznym” . Listy z przeglądu fizycznego . 127 (12): 126405. arXiv : 2012.02475 . Bibcode : 2021PhRvL.127l6405M . doi : 10.1103/PhysRevLett.127.126405 . ISSN 0031-9007    . PMID 34597066 . S2CID 227305789 .
  4. Bibliografia    _ Zhai, Dawei; Yao, Wang (2021-10-01). „Kontrola skrętu i heteroodkształcenia właściwości optycznych minipasm ekscytonów mory” . Materiały 2D . 8 (4): 044016. arXiv : 2110.01487 . Bibcode : 2021TDM.....8d4016Z . doi : 10.1088/2053-1583/ac2d16 . ISSN 2053-1583 . S2CID 238259645 .
  5. ^ Kapfer, Maelle; Jessen, Bjarke S.; Eisele, Megan E.; Fu, Mateusz; Danielsen, Dorte R.; Darlington, Thomas P.; Moore, Samuel L.; Finney, Nathan R.; Marchewa, Ariane; Hsieh, Valerie; Majchrzak, Paulina; Jiang, Zhihao; Biswas, Deepnarayan; Dudin, Paweł; Avila, José (21.09.2022). „Programowanie wzorów mory w materiałach 2D przez zginanie”. arXiv : 2209.10696 [ cond-mat.mes-hall ].
  6. ^ Pena, Tara; Dey, Aditya; Chowdhury, Shoieb A.; Azizimanesz, Ahmad; Hou, Wenhui; Sewaket, Arfan; Watson, Carla L.; Askari, Hesam; Wu, Stephen M. (2022-10-07). „Inżynieria mory w heterostrukturach 2D z odkształceniem wywołanym procesem”. arXiv : 2210.03480 [ cond-mat.mes-hall ].
  7. ^ Engelke, Rebeka; Yoo, Hyobin; Carr, Stephen; Xu, Kevin; Cazeaux, Paweł; Allen, Richard; Valdivia, Andres Mier; Luskin, Mitchell; Kaxiras, Eftimios; Kim, Minhyong; Han, Jung Hoon; Kim, Filip (16.07.2022). „Nieabelowe defekty topologiczne i mapowanie odkształceń w materiałach mory 2D”. arXiv : 2207.05276 [ cond-mat.mes-hall ].
  8. Bibliografia     _ Magaud, L.; Le Quang, T.; Guisset, V.; David, P.; Kaplica, C.; Coraux, J. (2016). „Uniwersalna klasyfikacja skręconych, naprężonych i ścinanych supersieci grafenowych mory” . Raporty naukowe . 6 (1): 25670. arXiv : 1605.07356 . Bibcode : 2016NatSR...625670A . doi : 10.1038/srep25670 . ISSN 2045-2322 . PMC 4867435 . PMID 27181495 .
  9. ^   Kierelski Aleksander; McGilly, Leo J.; Kennes, Dante M.; Xian, Lede; Yankowitz, Mateusz; Chen, Shaowen; Watanabe, K.; Taniguchi, T.; Kochanie, James; dziekan, Cory; Rubio, Anioł (2019). „Zmaksymalizowane interakcje elektronów pod kątem magicznym w skręconym dwuwarstwowym grafenie” . Natura . 572 (7767): 95–100. ar Xiv : 1812.08776 . Bibcode : 2019Natur.572...95K . doi : 10.1038/s41586-019-1431-9 . ISSN 0028-0836 . PMID    31367030 . S2CID 199057045 .
  10. Bibliografia    _ Yankowitz, Mateusz; Fallahazad, Babak; Kang, Sangwoo; Movva, Hema CP; Huang, Shengqiang; Larentis, Stefano; Corbet, Chris M.; Taniguchi, Takashi; Watanabe, Kenji; Banerjee, Sanjay K. (2016-03-09). „Heterostruktury van der Waalsa z wyrównaniem obrotowym o wysokiej dokładności” . Nano litery . 16 (3): 1989–1995. Bibcode : 2016NanoL..16.1989K . doi : 10.1021/acs.nanolett.5b05263 . ISSN 1530-6984 . PMID 26859527 .
  11. ^     Parker, Daniel E.; Soejima, Tomohiro; Hauschild, Johannes; Zaletel, Michael P.; Bultinck, Nick (2021-07-06). „Kwantowe przemiany fazowe wywołane odkształceniem w grafenie pod kątem magicznym” . Listy z przeglądu fizycznego . 127 (2): 027601. arXiv : 2012.09885 . Bibcode : 2021PhRvL.127b7601P . doi : 10.1103/PhysRevLett.127.027601 . ISSN 0031-9007 . OSTI 1821673 . PMID 34296891   . S2CID 229331622 .
  12. Bibliografia    _ Koshino, Mikito (14.06.2022). „Efekt zaburzenia mory w skręconym grafenie dwuwarstwowym” . Przegląd fizyczny B. 105 (24): 245408. arXiv : 2204.06177 . Bibcode : 2022PhRvB.105x5408N . doi : 10.1103/PhysRevB.105.245408 . ISSN 2469-9950 . S2CID 248157360 .
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Heterostrain&oldid=1140097737 ”