k -mer

Aby uzyskać szersze omówienie tego tematu, zobacz n-gram .
Sekwencja ATGG ma dwa 3-mery: ATG i TGG.

W bioinformatyce k -mery to podciągi o długości zawarte sekwencji biologicznej Stosowane głównie w kontekście genomiki obliczeniowej i analizy sekwencji , w których k -mery składają się z nukleotydów ( tj . A, T, G i C), k -mery są kapitalizowane w celu złożenia sekwencji DNA , poprawy ekspresji genów heterologicznych , identyfikować gatunki w próbkach metagenomicznych i tworzyć atenuowane szczepionki . Zwykle termin k -mer odnosi się do wszystkich sekwencji o długości tak że sekwencja AGAT miałaby cztery monomery (A, G, A i T), trzy 2-mery (AG, GA, AT), dwa 3-mery (AGA i GAT) i jeden 4-mer (AGAT). Mówiąc bardziej ogólnie, sekwencja o długości będzie miała k -mers i suma możliwych k -merów, gdzie jest w przypadku DNA ).

Wstęp

k -mery to po prostu . Na przykład wszystkie możliwe k -mery sekwencji DNA przedstawiono poniżej:

Przykładowe widmo 8-merów dla E. coli porównujące częstość występowania 8-merów ( tj. krotności) z liczbą ich wystąpień.
k -mery dla GTAGAGCTGT
k k -mery
1 G, T, A, G, A, G, C, T, G, T
2 GT, TA, AG, GA, AG, GC, CT, TG, GT
3 GTA, TAG, AGA, GAG, AGC, GCT, CTG, TGT
4 GTAG, TAGA, AGAG, GAGC, AGCT, GCTG, CTGT
5 GTAGA, TAGAG, AGAGC, GAGCT, AGCTG, GCTGT
6 GTAGAG, TAGAGC, AGAGCT, GAGCTG, AGCTGT
7 GTAGAGC, TAGAGCT, AGAGCTG, GAGCTGT
8 GTAGAGCT, TAGAGCTG, AGAGCTGT
9 GTAGAGCTG, TAGAGCTGT
10 GTAGAGCTGT

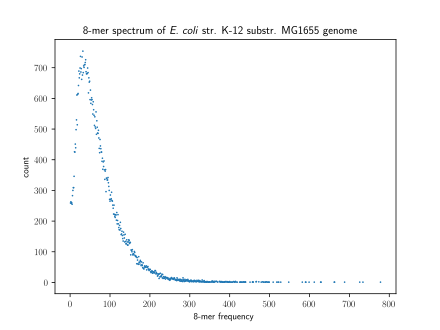
Metoda wizualizacji k -merów, widmo k -merów , pokazuje krotność każdego k -meru w sekwencji w porównaniu z liczbą k -merów z tą krotnością. Liczba modów w k -merowym dla genomu gatunku jest różna, przy czym większość gatunków ma rozkład jednomodalny. Jednak wszystkie ssaki mają dystrybucję multimodalną. Liczba modów w k -merów może się również różnić między regionami genomu: ludzie mają unimodalne widma k -merów w 5' UTR i eksony , ale multimodalne widma w 3' UTR i intronach .

Siły wpływające na DNA k -mer Częstotliwość

Na częstotliwość używania k -merów wpływa wiele sił, działających na wielu poziomach, które często pozostają ze sobą w konflikcie. Należy zauważyć, że na k -mery dla wyższych wartości k wpływają również siły oddziałujące na niższe wartości k . Na przykład, jeśli 1-mer A nie występuje w sekwencji, żaden z 2-merów zawierających A (AA, AT, AG i AC) również nie wystąpi, łącząc w ten sposób skutki różnych sił.

k = 1

Gdy k = 1, istnieją cztery k -mery DNA, tj . A, T, G i C. Na poziomie molekularnym między G i C są trzy wiązania wodorowe , podczas gdy między A i T są tylko dwa. GC wiązania, w wyniku dodatkowego wiązania wodorowego (i silniejszych interakcji w stosie), są bardziej stabilne termicznie niż wiązania AT. Ssaki i ptaki mają wyższy stosunek Gs i Cs do As i Ts ( zawartość GC ), co doprowadziło do hipotezy, że stabilność termiczna była czynnikiem napędzającym zmienność zawartości GC. Jednak, choć obiecująca, hipoteza ta nie sprawdziła się: analiza różnych prokariotów nie wykazała korelacji zawartości GC z temperaturą, jak przewidywałaby hipoteza adaptacji termicznej. Rzeczywiście, gdyby dobór naturalny miał być siłą napędową zmienności zawartości GC, wymagałoby to zmian pojedynczych nukleotydów , które często są ciche , aby zmienić sprawność organizmu.

Obecne dowody sugerują raczej, że konwersja genów ukierunkowana na GC (gBGC) jest czynnikiem napędzającym zmienność zawartości GC. gBGC to proces zachodzący podczas rekombinacji który zastępuje As i Ts przez Gs i Cs. Proces ten, chociaż różni się od doboru naturalnego, może jednak wywierać presję selekcyjną na DNA ukierunkowane na utrwalanie zamienników GC w genomie. gBGC można zatem postrzegać jako „oszusta” doboru naturalnego. Jak można się było spodziewać, zawartość GC jest większa w miejscach doświadczających większej rekombinacji. Ponadto organizmy o wyższych wskaźnikach rekombinacji wykazują wyższą zawartość GC, zgodnie z przewidywanymi efektami hipotezy gBGC. Co ciekawe, gBGC nie wydaje się ograniczać do eukariontów . Organizmy bezpłciowe, takie jak bakterie i archeony, również doświadczają rekombinacji poprzez konwersję genów, proces zastępowania sekwencji homologicznych, w wyniku którego powstaje wiele identycznych sekwencji w całym genomie. Ta rekombinacja jest w stanie zwiększyć zawartość GC we wszystkich domenach życia, co sugeruje, że gBGC jest powszechnie konserwowany. To, czy gBGC jest (przeważnie) neutralnym produktem ubocznym molekularnej maszynerii życia, czy też samo podlega selekcji, pozostaje do ustalenia. Dokładny mechanizm i ewolucyjna zaleta lub wada gBGC nie są obecnie znane.

k = 2

Pomimo stosunkowo dużej ilości literatury omawiającej odchylenia dotyczące zawartości GC, stosunkowo niewiele napisano o odchyleniach dotyczących dinukleotydów. Wiadomo, że te tendencje dinukleotydowe są względnie stałe w całym genomie, w przeciwieństwie do zawartości GC, która, jak widać powyżej, może się znacznie różnić. To ważna informacja, której nie wolno przeoczyć. Gdyby stronniczość dinukleotydów podlegała naciskom wynikającym z translacji , wówczas występowałyby różne wzorce stronniczości dinukleotydów w kodowaniu i niekodowaniu regiony napędzane przez zmniejszoną wydajność translacyjną niektórych dinucelotydów. Ponieważ tak nie jest, można zatem wywnioskować, że siły modulujące odchylenie dinukleotydowe są niezależne od translacji. Kolejnym dowodem przeciwko naciskom translacyjnym wpływającym na stronniczość dinukleotydów jest fakt, że tendencje dinukleotydowe wirusów, które w dużej mierze opierają się na wydajności translacji, są kształtowane przez ich rodzinę wirusów bardziej niż przez ich gospodarzy, których maszynerię translacyjną przejmują wirusy.

Przeciwieństwem rosnącej zawartości GC gBGC jest supresja CG , która zmniejsza częstotliwość 2-merów CG z powodu deaminacji metylowanych dinukleotydów CG, co skutkuje zastąpieniem CG przez TG, zmniejszając w ten sposób zawartość GC . Ta interakcja podkreśla wzajemne powiązania między siłami oddziałującymi na k -mery dla różnych wartości k.

Interesującym faktem dotyczącym błędu dinukleotydowego jest to, że może on służyć jako pomiar „odległości” między filogenetycznie podobnymi genomami. Genomy par organizmów, które są blisko spokrewnione, mają więcej podobnych odchyleń dinukleotydowych niż między parami organizmów bardziej odlegle spokrewnionych.

k = 3

Istnieje dwadzieścia naturalnych aminokwasów , które są wykorzystywane do budowy białek kodowanych przez DNA. Jednak są tylko cztery nukleotydy. Dlatego nie może istnieć zgodność jeden do jednego między nukleotydami a aminokwasami. Podobnie jest 16 2-merów, co również nie jest wystarczające, aby jednoznacznie reprezentować każdy aminokwas. Jednak w DNA jest 64 różnych 3-merów, co wystarcza, aby jednoznacznie reprezentować każdy aminokwas. Te nienakładające się 3-mery nazywane są kodonami . Podczas gdy każdy kodon odwzorowuje tylko jeden aminokwas, każdy aminokwas może być reprezentowany przez wiele kodonów . Zatem ta sama sekwencja aminokwasowa może mieć wiele reprezentacji DNA. Co ciekawe, każdy kodon dla aminokwasu nie jest używany w równych proporcjach. Nazywa się to błędem wykorzystania kodonów (CUB). Gdy k = 3, należy dokonać rozróżnienia między rzeczywistą częstotliwością 3-merową a CUB. Na przykład sekwencja ATGGCA zawiera w sobie cztery 3-merowe słowa (ATG, TGG, GGC i GCA), podczas gdy zawiera tylko dwa kodony (ATG i GCA). Jednak CUB jest głównym czynnikiem napędzającym stronniczość użycia 3-merów (stanowiących do ⅓ tego, ponieważ ⅓ k - merów w regionie kodującym to kodony) i będzie głównym tematem tej sekcji.

Dokładna przyczyna zmienności między częstotliwościami różnych kodonów nie jest w pełni zrozumiała. Wiadomo, że preferencje kodonów są skorelowane z obfitością tRNA, przy czym kodony pasujące do bardziej obfitych tRNA są odpowiednio częstsze, a białka o większej ekspresji wykazują większą CUB. Sugeruje to, że selekcja pod kątem wydajności lub dokładności translacji jest siłą napędową zmienności CUB.

k = 4

Podobny do efektu obserwowanego w przypadku odchylenia dinukleotydowego, odchylenia tetranukleotydowe organizmów podobnych filogenetycznie są bardziej podobne niż między organizmami mniej spokrewnionymi. Dokładna przyczyna zmienności odchylenia tetranukleotydowego nie jest dobrze poznana, ale postawiono hipotezę, że jest wynikiem utrzymania stabilności genetycznej na poziomie molekularnym.

Aplikacje

Częstotliwość zestawu k -merów w genomie gatunku, w regionie genomowym lub w klasie sekwencji może być wykorzystana jako „sygnatura” leżącej u podstaw sekwencji. Porównanie tych częstotliwości jest obliczeniowo łatwiejsze niż dopasowanie sekwencji i jest ważną metodą w analizie sekwencji bez dopasowania . Może być również wykorzystany jako pierwszy etap analizy przed wyrównaniem.

Montaż sekwencji

Ten rysunek przedstawia proces dzielenia odczytów na mniejsze k -mery (w tym przypadku 4-mery), aby można je było wykorzystać na wykresie De Bruijna. (A) Pokazuje sekwencjonowanie początkowego segmentu DNA. (B) Pokazuje odczyty, które zostały wykonane w wyniku sekwencjonowania, a także pokazuje, w jaki sposób są wyrównane. Problem z tym wyrównaniem polega jednak na tym, że nakładają się one na k-2, a nie k-1 (co jest potrzebne w wykresach De Bruijna). (C) Pokazuje, że odczyty są podzielone na mniejsze 4-mery. (D) Odrzuca powtórzone 4-mery, a następnie pokazuje ich wyrównanie. Zauważ, że te k -mery pokrywają się o k-1 i mogą być następnie użyte w grafie De Bruijna.

W składaniu sekwencji k -mery są używane podczas konstruowania grafów De Bruijna . Aby utworzyć wykres De Bruijna, - 1 { w celu utworzenia wierzchołka . Odczyty generowane z sekwencjonowania nowej generacji będą zazwyczaj miały generowane różne długości odczytu. Na przykład czyta Illumina technologia sekwencjonowania przechwytuje odczyty 100-merów. Jednak problem z sekwencjonowaniem polega na tym, że w rzeczywistości generowane są tylko małe frakcje ze wszystkich możliwych 100-merów obecnych w genomie. Wynika to z błędów odczytu, ale co ważniejsze, z prostych luk w pokryciu, które występują podczas sekwencjonowania. Problem polega na tym, że te małe ułamki możliwych k -merów naruszają kluczowe założenie wykresów De Bruijna, że ​​wszystkie odczyty k -merów muszą nakładać się na sąsiednie k -mery w genomie o nie ma wszystkich możliwych k -merów).

Rozwiązaniem tego problemu jest podzielenie tych odczytów wielkości k -merów na mniejsze k -mery, tak aby powstałe mniejsze k -mery reprezentowały wszystkie możliwe k -mery o tym mniejszym rozmiarze, które są obecne w genomie. Ponadto podział k -merów na mniejsze rozmiary również pomaga złagodzić problem różnych początkowych długości odczytu. W tym przykładzie pięć odczytów nie uwzględnia wszystkich możliwych 7-merów genomu i jako taki nie można utworzyć wykresu De Bruijna. Ale kiedy zostaną podzielone na 4-mery, powstałe podsekwencje wystarczą do zrekonstruowania genomu za pomocą wykresu De Bruijna.

Poza bezpośrednim zastosowaniem do składania sekwencji, k -mery można również stosować do wykrywania nieprawidłowego składania genomu poprzez identyfikację k -merów, które są nadreprezentowane, co sugeruje obecność powtórzonych sekwencji DNA , które zostały połączone. Ponadto k -mery są również wykorzystywane do wykrywania zanieczyszczenia bakteryjnego podczas składania genomu eukariotycznego, co jest podejściem zapożyczonym z dziedziny metagenomiki.

Wybór rozmiaru k -meru

Wybór rozmiaru k -meru ma wiele różnych skutków dla składania sekwencji. Efekty te różnią się znacznie między k -merami o mniejszych i większych rozmiarach . Dlatego należy zrozumieć różne k -merów, aby wybrać odpowiedni rozmiar, który równoważy efekty. Efekty rozmiarów przedstawiono poniżej.

Niższe rozmiary k -merów
  • Mniejszy rozmiar k -merów zmniejszy ilość krawędzi przechowywanych na grafie i jako taki pomoże zmniejszyć ilość miejsca wymaganego do przechowywania sekwencji DNA.
  • Mniejsze rozmiary zwiększą szansę na nałożenie się wszystkich k -merów i jako takie będą miały wymagane podsekwencje do skonstruowania wykresu De Bruijna.
  • Jednak mając mniejsze k -mery, ryzykujesz również posiadanie wielu wierzchołków na grafie prowadzących do pojedynczego k-meru. W związku z tym utrudni to rekonstrukcję genomu, ponieważ istnieje wyższy poziom niejednoznaczności ścieżki ze względu na większą liczbę wierzchołków, które trzeba będzie pokonać.
  • Informacje są tracone, gdy k -mery stają się mniejsze.
    • Np. prawdopodobieństwo AGTCGTAGATGCTG jest niższe niż ACGT i jako takie zawiera większą ilość informacji ( więcej informacji można znaleźć w entropii (teorii informacji) .
  • Mniejsze k -mery mają również problem polegający na tym, że nie są w stanie rozdzielić obszarów DNA, w których występują małe mikrosatelity lub powtórzenia. Dzieje się tak, ponieważ mniejsze k -mery będą miały tendencję do siedzenia całkowicie w regionie powtórzeń i dlatego trudno jest określić ilość powtórzeń, które faktycznie miały miejsce.
    • Np. dla podsekwencji ATGTGTGTGTGTGTACG, ilość powtórzeń TG zostanie utracona, jeśli zostanie wybrany k -mer o rozmiarze mniejszym niż 16. To dlatego, że większość k -mery będą znajdować się w powtórzonym regionie i mogą zostać po prostu odrzucone jako powtórzenia tego samego k -meru zamiast odnosić się do liczby powtórzeń.
Wyższe rozmiary k -merów
  • Posiadanie k -merów o większych rozmiarach zwiększy liczbę krawędzi na wykresie, co z kolei zwiększy ilość pamięci potrzebnej do przechowywania sekwencji DNA.
  • Zwiększając rozmiar k -merów, zmniejszy się również liczba wierzchołków. Pomoże to w konstrukcji genomu, ponieważ na wykresie będzie mniej ścieżek do przejścia.
  • Większe k -mery również wiążą się z większym ryzykiem braku zewnętrznych wierzchołków z każdego k-meru. Wynika to z większych k -merów zwiększających ryzyko, że nie będzie się pokrywać z innym k -merem o . Dlatego może to prowadzić do rozbieżności w odczytach i jako takie może prowadzić do większej liczby mniejszych kontigów .
  • Większe rozmiary k -merów pomagają złagodzić problem małych regionów powtórzeń. Wynika to z faktu, że k -mer będzie zawierał równowagę regionu powtórzeń i przylegających sekwencji DNA (biorąc pod uwagę, że są wystarczająco duże), co może pomóc w rozwiązaniu ilości powtórzeń w tym konkretnym obszarze.

Genetyka i genomika

W odniesieniu do choroby, błąd dinukleotydowy został zastosowany do wykrywania wysp genetycznych związanych z patogenicznością. Wcześniejsze prace wykazały również, że tendencje tetranukleotydowe są w stanie skutecznie wykrywać poziomy transfer genów zarówno u prokariotów, jak i eukariontów.

Innym zastosowaniem k -merów jest taksonomia oparta na genomice. Na przykład zawartość GC została wykorzystana do rozróżnienia gatunków Erwinia z umiarkowanym sukcesem. Podobne do bezpośredniego wykorzystania zawartości GC do celów taksonomicznych jest użycie Tm , temperatury topnienia DNA. Ponieważ wiązania GC są bardziej stabilne termicznie, sekwencje o wyższej zawartości GC wykazują wyższą Tm . W 1987 roku komitet ad hoc ds. uzgadniania podejść do systematyki bakteryjnej zaproponował wykorzystanie ΔT m jako czynnika do określania granic gatunków w ramach koncepcja gatunku filogenetycznego , chociaż wydaje się, że ta propozycja nie zyskała popularności w społeczności naukowej.

Inne zastosowania w genetyce i genomice obejmują:

Metagenomika

k -merów jest intensywnie wykorzystywana w metagenomice zarówno do analizy, jak i kategoryzowania. W binowaniu wyzwaniem jest rozdzielenie odczytów sekwencjonowania na „kosze” odczytów dla każdego organizmu (lub operacyjnej jednostki taksonomicznej ), które następnie zostaną złożone. TETRA to godne uwagi narzędzie, które pobiera próbki metagenomiczne i grupuje je w organizmy na podstawie ich częstotliwości tetranukleotydowych ( k = 4). Inne narzędzia, które podobnie opierają się na k -merów do kategoryzacji metagenomicznej, to CompostBin ( k = 6), PCAHIER, PhyloPythia (5 ≤ k ≤ 6), CLARK ( k ≥ 20) i TACOA (2 ≤ k ≤ 6). Ostatnie osiągnięcia zastosowały również głębokie uczenie się do kategoryzowania metagenomicznego przy użyciu k -merów.

Inne zastosowania w ramach metagenomiki obejmują:

  • Odzyskiwanie ramek odczytu z surowych odczytów
  • Szacowanie liczebności gatunków w próbkach metagenomicznych
  • Określenie, które gatunki są obecne w próbkach
  • Identyfikacja biomarkerów chorób z próbek

Biotechnologia

Modyfikowanie częstotliwości k -merów w sekwencjach DNA było szeroko stosowane w zastosowaniach biotechnologicznych do kontrolowania wydajności translacji. W szczególności był używany zarówno do regulacji w górę, jak iw dół tempa produkcji białka.

W odniesieniu do zwiększania produkcji białek, zastosowano zmniejszanie niekorzystnej częstości dinukleotydów, co daje wyższe szybkości syntezy białek. Ponadto zmodyfikowano błąd wykorzystania kodonów, aby utworzyć sekwencje synonimiczne o większej szybkości ekspresji białka. Podobnie optymalizacja par kodonów, połączenie optymalizacji dinucelotydu i kodonów, została również z powodzeniem zastosowana do zwiększenia ekspresji.

Najbardziej zbadanym zastosowaniem k -merów do zmniejszania wydajności translacji jest manipulacja parami kodonów w celu osłabienia wirusów w celu stworzenia szczepionek. Naukowcom udało się przekodować wirusa dengi , wirusa wywołującego gorączkę denga , tak że jego tendencja do par kodonów różniła się bardziej od preferencji ssaków w zakresie wykorzystania kodonów niż typu dzikiego. Chociaż zawierał identyczną sekwencję aminokwasów, przekodowany wirus wykazywał znacznie osłabioną patogeniczność jednocześnie wywołując silną odpowiedź immunologiczną. Podejście to zostało również skutecznie wykorzystane do stworzenia szczepionki przeciw grypie, a także szczepionki przeciwko herpeswirusowi choroby Marka (MDV). Warto zauważyć, że manipulacja parą kodonów zastosowana do osłabienia MDV nie zmniejszyła skutecznie onkogenności wirusa , co podkreśla potencjalną słabość zastosowań biotechnologicznych tego podejścia. Do tej pory żadna szczepionka z dezoptymalizowanymi parami kodonów nie została zatwierdzona do użytku.

Dwa późniejsze artykuły pomagają wyjaśnić rzeczywisty mechanizm leżący u podstaw deoptymalizacji par kodonów: błąd par kodonów jest wynikiem błędu dinukleotydów. Badając wirusy i ich żywicieli, autorzy obu zestawów byli w stanie stwierdzić, że mechanizm molekularny, który powoduje atenuację wirusów, polega na zwiększeniu liczby dinukleotydów słabo nadających się do translacji.

Zawartość GC, ze względu na jej wpływ na temperaturę topnienia DNA , jest wykorzystywana do przewidywania temperatury hybrydyzacji w PCR , innym ważnym narzędziu biotechnologicznym.

Realizacja

Pseudo kod

Określenie możliwych k -merów odczytu można wykonać, po prostu zmieniając długość łańcucha o jeden i usuwając każdy podciąg o długości . Pseudokod do osiągnięcia tego jest następujący: 

 
    
     procedura  k-mers(string seq, integer k)  is  L ← length(seq) arr ← nowa tablica L − k + 1 puste łańcuchy  // iteracja po liczbie k-merów w seq,  // przechowywanie n-tego k- mer w tablicy wyjściowej  dla  n ← 0  do  L − k + 1 wyłączne  do  arr[n] ← podsekwencja seq od litery n włącznie do litery n + k wyłączna  powrót  arr

W rurociągach bioinformatycznych

Ponieważ liczba k -merów rośnie wykładniczo dla wartości k , liczenie k -merów dla dużych wartości k (zwykle >10) jest zadaniem trudnym obliczeniowo. Chociaż proste implementacje, takie jak powyższy pseudokod, działają dla małych wartości k , należy je dostosować do aplikacji o dużej przepustowości lub gdy k jest duże. Aby rozwiązać ten problem, opracowano różne narzędzia:

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=K-mer&oldid=1136641099 ”