Loxodromiczna sekwencja stycznych okręgów Coxetera

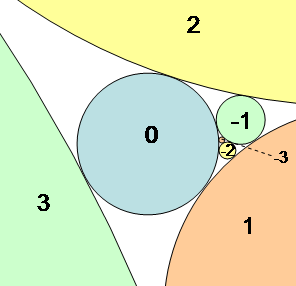
Niebieski okrąg 0 jest styczny do okręgów 1, 2 i 3, a także do poprzednich okręgów −1, −2 i −3.

W geometrii loxodromiczna sekwencja stycznych okręgów Coxetera jest nieskończoną sekwencją okręgów ułożonych w taki sposób, że dowolne cztery kolejne okręgi w sekwencji są parami wzajemnie styczne . Oznacza to, że każdy okrąg w sekwencji jest styczny do trzech okręgów, które go poprzedzają, a także do trzech okręgów, które po nim następują.

Nieruchomości

Promienie okręgów w sekwencji tworzą postęp geometryczny ze stosunkiem

$${\ Displaystyle k = \ varphi + {\ sqrt {\ varphi}} \ około 2,89005 \,}$$

gdzie jest złotym podziałem . φ $\ displaystyle \ varphi}$ Ten stosunek $odwrotność$ spełniają równanie

$${\ Displaystyle (1 + x + x ^ {2} + x ^ {3}) ^ {2 }=2(1+x^{2}+x^{4}+x^{6})\ ,}$$

więc dowolne cztery kolejne okręgi ciągu spełniają warunki twierdzenia Kartezjusza .

Środki okręgów w sekwencji leżą na spirali logarytmicznej . Patrząc od środka spirali, kąt między środkami kolejnych okręgów wynosi

$${\ Displaystyle \ cos ^ {-1} \ lewo ({\ Frac {-1} {\ varphi}} \ prawej) \ około 128,173 ^ {\ circ} \ .}$$

Kąt między kolejnymi trójkami środków wynosi

$${\ Displaystyle \ theta = \ cos ^ {- 1} {\ Frac {1} {\ varphi}} \ około 51,8273 ^ {\ circ},}$$

taki sam jak jeden z kątów trójkąta Keplera , trójkąta prostokątnego, którego konstrukcja obejmuje również pierwiastek kwadratowy złotego podziału.

Historia i związane z nią konstrukcje

Konstrukcja została nazwana na cześć geometra HSM Coxetera , który uogólnił przypadek dwuwymiarowy na sekwencje sfer i hipersfer w wyższych wymiarach. Można to interpretować jako zdegenerowany przypadek szczególny spirali Doyle'a .

Zobacz też

• uszczelka apollińska

Linki zewnętrzne

• Weisstein, Eric W. , „Loxodromiczna sekwencja stycznych okręgów Coxetera” , MathWorld