Licznik schodkowy

Replika schodkowego licznika Leibniza w Deutsches Museum.

... marnowanie czasu na obliczenia jest poniżej godności doskonałych ludzi, kiedy każdy chłop mógłby wykonać pracę równie dokładnie za pomocą maszyny.

— Gottfried Leibniz

Licznik schodkowy lub kalkulator Leibniza był kalkulatorem mechanicznym wynalezionym przez niemieckiego matematyka Gottfrieda Wilhelma Leibniza około 1672 r. I ukończonym w 1694 r. Nazwa pochodzi od tłumaczenia niemieckiego terminu określającego jego mechanizm operacyjny, Staffelwalze , oznaczającego „bęben schodkowy”. Był to pierwszy kalkulator, który mógł wykonywać wszystkie cztery operacje arytmetyczne .

Jego skomplikowana, precyzyjna przekładnia była jednak nieco poza ówczesną technologią produkcji; problemy mechaniczne, oprócz wady konstrukcyjnej mechanizmu nośnego, uniemożliwiły niezawodną pracę maszyn.

Zbudowano dwa prototypy; dziś tylko jeden przetrwał w Bibliotece Narodowej Dolnej Saksonii ( Niedersächsische Landesbibliothek ) w Hanowerze w Niemczech. Na wystawie znajduje się kilka późniejszych replik, na przykład ta w Deutsches Museum w Monachium . Pomimo mechanicznych wad schodkowego licznika, sugerował on możliwości przyszłym konstruktorom kalkulatorów. Mechanizm operacyjny, wynaleziony przez Leibniza, zwany cylindrem schodkowym lub kołem Leibniza , był używany w wielu maszynach liczących przez 200 lat, a do lat 70. XX wieku wraz z kalkulatorem ręcznym Curta .

Opis

Dalsze informacje: koło Leibniza
Rysunek schodkowego licznika z 1897 Meyers Konversations-Lexikon , przedstawiający wersję 12-cyfrową

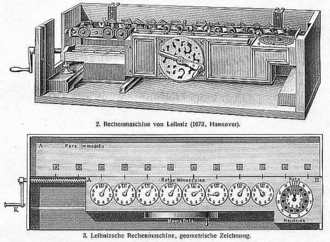
Licznik schodkowy był oparty na mechanizmie zębatym, który wynalazł Leibniz i który obecnie nazywa się kołem Leibniza . Nie jest jasne, ile różnych wariantów kalkulatora powstało. Niektóre źródła, takie jak rysunek po prawej, pokazują wersję 12-cyfrową. Ta sekcja opisuje zachowany 16-cyfrowy prototyp w Hanowerze .


Koło Leibniza W pokazanym położeniu koło liczące zazębia się z 3 z 9 zębów koła Leibniza

Maszyna o długości około 67 cm (26 cali), wykonana z polerowanego mosiądzu i stali, osadzona w dębowej skrzyni. Składa się z dwóch połączonych równolegle części: akumulatora z tyłu, która może pomieścić 16 cyfr dziesiętnych, oraz 8-cyfrowej sekcji wejściowej z przodu. Sekcja wejściowa ma 8 pokręteł z pokrętłami do ustawiania operandu numer telefonu, pokrętło przypominające telefon po prawej stronie, aby ustawić cyfrę mnożnika, oraz korbkę z przodu, aby wykonać obliczenia. Wynik pojawia się w 16 okienkach tylnej sekcji akumulatora. Sekcja wejściowa jest zamontowana na szynach i może być przesuwana wzdłuż sekcji akumulatora za pomocą korby na lewym końcu, która obraca przekładnię ślimakową, aby zmienić ustawienie cyfr operandu z cyframi akumulatora. Istnieje również wskaźnik przenoszenia dziesiątek i kontrola ustawienia maszyny na zero. Maszyna może:

  • dodać lub odjąć liczbę 8-cyfrową do/od liczby 16-cyfrowej,
  • pomnóż dwie liczby 8-cyfrowe, aby uzyskać wynik 16-cyfrowy,
  • podzielić liczbę 16-cyfrową przez dzielnik 8-cyfrowy.

Dodawanie lub odejmowanie odbywa się w jednym kroku, za pomocą obrotu korby. Mnożenie i dzielenie są wykonywane cyfra po cyfrze na cyfrach mnożnika lub dzielnika, w procedurze odpowiadającej znanym długiego mnożenia i długiego dzielenia nauczanym w szkole. Sekwencje tych operacji można wykonać na liczbie w akumulatorze; na przykład może obliczać pierwiastki za pomocą serii dzieleń i dodawania.

Historia

Stopniowy mechanizm liczący ze zdjętą obudową
Dalsze informacje: Prekursory kalkulatora mechanicznego

Leibniz wpadł na pomysł maszyny liczącej w 1672 roku w Paryżu, od krokomierza . Później dowiedział się o Blaise'a Pascala , kiedy czytał Myśli Pascala . Skoncentrował się na rozszerzeniu mechanizmu Pascala, aby mógł się mnożyć i dzielić. Przedstawił drewniany model Towarzystwu Królewskiemu w Londynie 1 lutego 1673 r. I otrzymał wiele zachęt. W liście z 26 marca 1673 r. do Johanna Friedricha , w którym wspomniał o prezentacji w Londynie, Leibniz opisał przeznaczenie „maszyny arytmetycznej” jako wykonywanie obliczeń” leicht, geschwind, gewiß " [ sic ], czyli łatwo, szybko i niezawodnie. Leibniz dodał również, że teoretycznie obliczone liczby mogą być tak duże, jak potrzeba, jeśli rozmiar maszyny zostanie dostosowany; cytuję: " eine zahl von einer ganzen Reihe Ziphern, sie sey so lang sie wolle (nach ratio der größe der Machine) " [ sic ]. W języku angielskim: „liczba składająca się z szeregu cyfr, tak długo, jak to możliwe (proporcjonalnie do wielkości maszyny)”. Jego pierwsza wstępna maszyna mosiężna została zbudowana w latach 1674-1685. Jego tak zwana starsza maszyna została zbudowana w latach 1686-1694. „Młodsza maszyna”, ocalała maszyna, została zbudowana w latach 1690-1720.

W 1775 roku „młodsza maszyna” została wysłana do naprawy na Uniwersytecie w Getyndze i została zapomniana. W 1876 r. ekipa robotników znalazła go w pokoju na poddaszu budynku uniwersyteckiego w Getyndze . Wrócił do Hanoweru w 1880 r. Od 1894 do 1896 r. Artur Burkhardt, założyciel dużej niemieckiej firmy produkującej kalkulatory, odrestaurował go i od tego czasu jest przechowywany w Niedersächsische Landesbibliothek.

Operacja

Maszyna wykonuje mnożenie przez wielokrotne dodawanie i dzielenie przez wielokrotne odejmowanie. Podstawową operacją wykonywaną jest dodawanie (lub odejmowanie) operandu do rejestru akumulatora dowolną ilość razy (w celu odjęcia obraca się korbę roboczą w przeciwnym kierunku). Liczba dodawania (lub odejmowania) jest kontrolowana przez tarczę mnożnika. Działa jak tarcza telefoniczna , z dziesięcioma otworami na obwodzie ponumerowanymi od 0 do 9. Aby pomnożyć przez pojedynczą cyfrę, 0–9, rysik w kształcie gałki wkłada się do odpowiedniego otworu w tarczy i obraca korbą. Tarcza mnożnika obraca się zgodnie z ruchem wskazówek zegara, maszyna wykonuje jedno dodawanie dla każdego otworu, aż rysik zatrzyma się w górnej części tarczy. Wynik pojawia się w oknach akumulatora. Powtarzane odejmowania są wykonywane podobnie, z wyjątkiem tego, że tarcza mnożnika obraca się w przeciwnym kierunku, więc używany jest drugi zestaw cyfr w kolorze czerwonym. Aby wykonać pojedyncze dodawanie lub odejmowanie, mnożnik jest po prostu ustawiany na jeden.

Aby pomnożyć przez liczby powyżej 9:

  1. Mnożnik jest ustawiony na tarczach operandów.
  2. Pierwsza (najmniej znacząca) cyfra mnożnika jest ustawiana na tarczy mnożnika jak wyżej i kręcona korbą mnoży operand przez tę cyfrę i umieszcza wynik w akumulatorze.
  3. Sekcja wejściowa jest przesuwana o jedną cyfrę w lewo za pomocą korby końcowej.
  4. Na tarczy mnożnika ustawia się następną cyfrę mnożnika i ponownie obraca się korbą, mnożąc operand przez tę cyfrę i dodając wynik do akumulatora.
  5. Powyższe 2 kroki są powtarzane dla każdej cyfry mnożnika. Na koniec wynik pojawia się w oknach akumulatora.

W ten sposób operand można pomnożyć przez dowolną liczbę, chociaż wynik jest ograniczony pojemnością akumulatora.

Aby podzielić przez wielocyfrowy dzielnik, stosuje się ten proces:

  1. Dzielna jest ustawiana w akumulatorze, a dzielnik jest ustawiany na tarczach argumentów.
  2. Sekcja wejściowa jest przesuwana za pomocą korby końcowej, aż lewe cyfry dwóch liczb zrównają się.
  3. Korba operacji jest obracana, a dzielnik jest wielokrotnie odejmowany od akumulatora, aż lewa (najbardziej znacząca) cyfra wyniku będzie równa 0 [ potrzebne źródło ] . Liczba wyświetlana na tarczy mnożnika jest wtedy pierwszą cyfrą ilorazu.
  4. Sekcja wejściowa jest przesunięta w prawo o jedną cyfrę.
  5. Powyższe dwa kroki są powtarzane, aby uzyskać każdą cyfrę ilorazu, aż karetka wejściowa dotrze do prawego końca akumulatora.

Można zauważyć, że te procedury są po prostu zmechanizowanymi wersjami długiego dzielenia i mnożenia .

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Stepped_reckoner&oldid=1116569063 ”