Matryca kurtki

W matematyce macierz płaszcza jest $i$ macierzą symetryczną rzędu n , jeśli jej wpisy rzeczywiste , ze skończonego , I

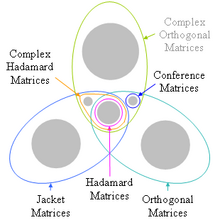
Hierarchia typów macierzy

{\ Displaystyle \ AB = BA = I_ {n}}

gdzie I _n jest macierzą tożsamościową , oraz

{\ Displaystyle \ B = {1 \ ponad n} (a_ {ij} ^ {-1}) ^ {T}.}

gdzie T oznacza transpozycję macierzy.

Innymi słowy, odwrotność macierzy płaszcza jest określana jako jej odwrotność elementarna lub blokowa. Powyższą definicję można również wyrazić jako:

{\ Displaystyle \ forall u, v \ in \ {1,2, \ kropki, n \}: ~ a_ {iu}, a_ {iv} \ neq 0, ~~~~ \ suma _ {i = 1} ^ {n}a_{iu}^{-1}\,a_{iv}={\begin{przypadki}n,&u=v\\0,&u\neq v\end{przypadki}}}

Macierz płaszcza jest uogólnieniem macierzy Hadamarda ; jest to przekątna macierz odwrotna blokowa.

Motywacja

N	.... −2, −1, 0 1, 2,.....	logarytm
2 ^przyp	.... ${\ Displaystyle \ {1 \ ponad 4}, {1 \ ponad 2},}$ 1, 2, 4, ...	seria

Jak pokazano w tabeli, tj. W szeregu, na przykład z n = 2, do przodu: ${\ Displaystyle 2 ^ {2} = 4}$ , odwrotność : ${\ Displaystyle (2 ^ {2}) ^ {-1} = {1 \ ponad 4}}$ 4 $\ Displaystyle 4 * {1 \ ponad 4} = 1}$ . Oznacza to, że istnieje elementarna odwrotność.

Przykład 1.

\ Displaystyle A = \ lewo [{\ rozpocząć {tablica} {rrrr} 1 i 1 i 1 i 1 \\ 1 i - 2 i 2 i -1\\1&2&-2&-1\\1&-1&-1&1\\\end{tablica}}\right],}

{\ Displaystyle B = {1 \ ponad 4} \ lewo [{\ rozpocząć {tablica} {rrrr} 1 i 1 i 1 i 1 \\ [6pt] 1 i - {1 \ ponad 2} i {1 \ ponad 2} i -1 \\ [ 6pt]1&{1 \over 2}&-{1 \over 2}&-1\\[6pt]1&-1&-1&1\\[6pt]\end{array}}\right].}

B

lub bardziej ogólne

{\ Displaystyle A = \ lewo [{\ rozpocząć {tablica} {rrrr} a&b&b&a\\b&-c&c& -b\\b&c&-c&-b\\a&-b&-b&a\end{tablica}}\right],}

:

{\ Displaystyle B = {1 \ ponad 4} \ lewo [{\ rozpocząć {tablica} {rrrr} {1 \ ponad a} i {1 \ ponad b} i {1 \ ponad b} i {1 \ ponad a} \\[6pt]{1 \over b}&-{1 \over c}&{1 \over c}&-{1 \over b}\\[6pt]{1 \over b}&{1 \over c}&-{1 \over c}&-{1 \over b}\\[6pt]{1 \over a}&-{1 \over b}&-{1 \over b}&{1 \over a}\end{tablica}}\right],}

Przykład 2.

W przypadku macierzy mxm ${\ Displaystyle \ mathbf {A_ {j}}}$

$operatorname {diag} (A_ {1}, A_ {2}, ..A_ {n})}$ oznacza macierz Jacket o przekątnej mn x mn.

{\ Displaystyle J_ {4} = \ lewo [{\ rozpocząć {tablica} {rrrr} I_ {2} i 0 i 0 i 0 \\ 0&\cos \theta &-\sin \theta &0\\0&\sin \theta &\cos \theta &0\\0&0&0&I_{2}\end{array}}\right],}

{\ Displaystyle \ J_ {4} ^ {T} J_ {4} = J_ {4} J_ {4} ^ {T} = I_ {4}.}

Przykład 3.

Wzór Eulera :

{\ Displaystyle e ^ {i \ pi} + 1 = 0}

,

{\ Displaystyle e ^ {i \ pi} = \ cos {\ pi} + i \ sin {\ pi} = -1}

i

{\ Displaystyle e ^ {-i \ pi} = \ sałata {\ pi } -i\sin {\pi}=-1}

.

Dlatego,

{\ Displaystyle e ^ {i \ pi} e ^ {-i \ pi} = (-1) ({\ Frac {1} -1}})=1}

.

Również,

{\ Displaystyle y = e ^ {x}}

{\ Displaystyle {\ Frac {dy} {dx}} = e ^ {x}}

,

{\ Displaystyle {\ Frac {dy} {dx}}} {\ Frac {dx} {dy}} = e ^ {x} {\ Frac {1} {e ^ {x} }}=1}

.

Wreszcie,

A · B = B · A = ja

Przykład 4.

 Rozważmy, że  ${\ Displaystyle [\ mathbf {A}] _ {N}}$  być macierzami blokowymi 2x2 rzędu  ${\ Displaystyle N = 2p}$

{\ Displaystyle [\ mathbf {A}] _ {N} = \ lewo [{\ rozpocząć {tablica} {rrrr} \ mathbf {A} _ {0} i \ mathbf {A} _ {1}

.

$}}$ ZA i ${\ Displaystyle [\ mathbf {A} _ {1}] _ {p}}$ są pxp Macierz płaszcza, to $jest$ blokową macierzą krążącą wtedy i tylko wtedy, gdy ${ 0}\mathbf {A} _{1}^{rt}+\mathbf {A} _{1}^{rt}\mathbf {A} _{0}}$ , gdzie rt oznacza odwrotną transpozycję.

Przykład 5.

Niech ${\ Displaystyle \ mathbf {A} _ {0} = \ lewo [{\ rozpocząć {tablica} {rrrr} -1 i 1 \\ 1 i 1 \\\ koniec {tablica}} \ prawo],}$ i ${\ Displaystyle \ mathbf {A} _ {1} = \ lewo [{\ rozpocząć {tablica} {rrrr} -1 i -1 \\- 1&1\\\end {tablica}}\right],}$ , następnie macierz ${\ Displaystyle [\ mathbf {A}] _ {N}}$ jest dany przez

{\ Displaystyle [\ mathbf {A} ]_{4}=\left[{\begin{tablica}{rrrr}\mathbf {A} _{0}&\mathbf {A} _{1}\\\mathbf {A} _{0}&\ mathbf {A} _{1}\\\end{tablica}}\right]=\left[{\begin{tablica}{rrrr}-1&1&-1&-1\\1&1&-1&1\\-1&1&-1&- 1\\1&1&-1&1\\\koniec {tablica}}\prawo],}

,

{\ Displaystyle [\ mathbf {A}] _ {4}}

⇒

{\ Displaystyle \ lewo [ {\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]^{T}\otimes \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right ]\otimes \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]^{T},}

gdzie U , C , ZA , G oznacza ilość zasad nukleinowych DNA, a macierz $jest krążącą$ która prowadzi do zasady Antagonizm z matrycą kodu genetycznego Nirenberga.

[1] Moon Ho Lee, „Centralnie ważona transformacja Hadamarda”, IEEE Transactions on Circuits Syst. Tom. 36, nr 9, s. 1247-1249, wrzesień 1989.

[2] Kathy Horadam, Matryce Hadamarda i ich zastosowania , Princeton University Press, Wielka Brytania, rozdział 4.5.1: Konstrukcja matrycy płaszcza, PP. 85–91, 2007.

[3] Moon Ho Lee, Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing , wydawnictwo LAP LAMBERT, Niemcy, listopad 2012 r.

[4] Moon Ho Lee i inni. al., „Metoda i system komunikacji MIMO z wykorzystaniem matrycy blokowej obiegowej płaszcza”, patent USA, nr. USA 009356671B1, maj 2016 r.

[5] SK Lee i MH Lee, „The COVID-19 DNA-RNA Genetic Code Analysis using Information Theory of Double Stochastic Matrix”, IntechOpen, Book Chapter, 17 kwietnia 2022 r. [Dostępne w Internecie: https://www . intechopen.com/chapters/81329 ].

Linki zewnętrzne