Metoda Romberga

Ten artykuł dotyczy metody całkowania numerycznego. Aby zapoznać się z manewrem badania neurologicznego, zobacz test Romberga .

W analizie numerycznej do oszacowania całki oznaczonej stosuje się metodę Romberga

$${\ Displaystyle \ int _ {a} ^ {b} f (x) \, dx}$$

poprzez wielokrotne stosowanie ekstrapolacji Richardsona na zasadzie trapezu lub reguły prostokąta (reguła punktu środkowego). Szacunki generują tablicę trójkątną . Metoda Romberga jest formułą Newtona-Cotesa - ocenia całkę w równomiernie rozmieszczonych punktach. Całka musi mieć ciągłe pochodne, chociaż całkiem dobre wyniki można uzyskać, jeśli istnieje tylko kilka pochodnych. Jeśli możliwe jest oszacowanie całki w nierówno rozmieszczonych punktach, wówczas inne metody, takie jak kwadratura Gaussa i kwadratura Clenshawa – Curtisa są na ogół dokładniejsze.

Metoda nosi imię Wernera Romberga (1909–2003), który opublikował ją w 1955 roku.

metoda

Używając ${\ textstyle h_ {n} = {\ frac {(ba)}} {2^ {n}}}}$ , metodę można zdefiniować indukcyjnie przez

$${\ Displaystyle {\ rozpocząć {wyrównane} R (0,0) & = h_ {1} (f (a) + f (b))\\R(n,0)&={\tfrac {1}{2}}R(n-1,0)+h_{n}\suma _{k=1}^{2^{ n-1}}f(a+(2k-1)h_{n})\\R(n,m)&=R(n,m-1)+{\tfrac {1}{4^{m}- 1}}(R(n,m-1)-R(n-1,m-1))\\&={\frac {1}{4^{m}-1}}(4^{m} R(n,m-1)-R(n-1,m-1))\end{wyrównane}}}$$

gdzie ${\ Displaystyle n \ geq m}$ i ${\ Displaystyle m \ geq 1 \,}$ . W notacji dużego O błąd dla R ( n , m ) wynosi: ${\ Displaystyle O \ lewo (h_ {n} ^ {2m + 2} \ prawo).}$

Ekstrapolacja zerowa, R ( n , 0) , jest równoważna regule trapezów z 2 ⁿ + 1 punktami; pierwsza ekstrapolacja R ( n , 1) jest równoważna regule Simpsona z 2 ⁿ + 1 punktami. Druga ekstrapolacja, R ( n , 2) , jest równoważna regule Boole'a z 2 ⁿ + 1 zwrotnica. Dalsze ekstrapolacje różnią się od wzorów Newtona-Cotesa. W szczególności dalsze ekstrapolacje Romberga rozszerzają regułę Boole'a w bardzo nieznaczny sposób, modyfikując wagi do stosunków podobnych jak w regule Boole'a. W przeciwieństwie do tego, dalsze metody Newtona-Cotesa dają coraz bardziej zróżnicowane wagi, ostatecznie prowadząc do dużych dodatnich i ujemnych wag. Wskazuje to, jak wielomianowe metody Newtona-Cotesa z interpolacją dużego stopnia nie są zbieżne dla wielu całek, podczas gdy integracja Romberga jest bardziej stabilna.

Oznaczając nasze przybliżenia jako ${$$\ textstyle A_ {0} {\ big (} {\ frac {h}$ zamiast ${\ textstyle R (n, 0)}$ , możemy przeprowadzić ekstrapolację Richardsona ze wzorem błędu zdefiniowanym poniżej:

$${\ Displaystyle \ int _ {a} ^ {b} f (x) \, dx = A_ {0} {\ bigg {} {\ Frac {h} {2 ^ {n}}} {\ bigg)} + a_{0}{\bigg (}{\frac {h}{2^{n}}}{\bigg)}^{2}+a_{1}{\bigg (}{\frac {h}{2 ^{n}}}{\bigg )}^{4}+a_{2}{\bigg (}{\frac {h}{2^{n}}}{\bigg)}^{6}+\ kropki }$$

$\$ uzyskaliśmy $przybliżenia$ ZA , możemy je oznaczyć jako ${\ textstyle R (n, m)}$ .

Gdy oszacowanie funkcji jest kosztowne, może być korzystne zastąpienie interpolacji wielomianowej Richardsona interpolacją racjonalną zaproponowaną przez Bulirscha i Stoera (1967) .

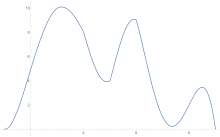
Przykład geometryczny

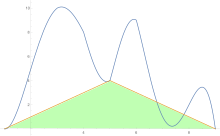
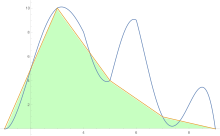
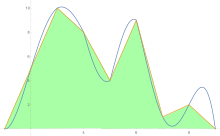
Aby oszacować pole pod krzywą, reguła trapezów jest stosowana najpierw do jednego kawałka, potem do dwóch, potem do czterech i tak dalej.

Jeden kawałek. Uwaga, ponieważ zaczyna się i kończy na zero, to przybliżenie daje zerowy obszar.

Dwa kawałki

Czteroczęściowy

Ośmioczęściowy

Po uzyskaniu oszacowań z reguły trapezów stosowana jest ekstrapolacja Richardsona .

• W pierwszej iteracji estymatory dwuczęściowe i jednoczęściowe są używane we wzorze (4 × (dokładniejsze) − (mniej dokładne))/3 Ten sam wzór jest następnie używany do porównania estymacji czteroczęściowej i dwuczęściowej, i podobnie dla wyższych szacunków
• Dla drugiej iteracji wartości z pierwszej iteracji są używane we wzorze (16(dokładniej) − mniej dokładnie))/15
• Trzecia iteracja wykorzystuje następną potęgę 4: (64 (dokładniej) - mniej dokładnie))/63 na wartościach uzyskanych w drugiej iteracji.
• Wzór jest kontynuowany, aż pojawi się jedno oszacowanie.

Liczba części	Szacunki trapezowe	Pierwsza iteracja	Druga iteracja	Trzecia iteracja
		(4 MA - LA)/3*	(16 MA - LA)/15	(64 MA - LA)/63
1	0	(4×16 − 0)/3 = 21,333...	(16×34,667 - 21,333)/15 = 35,556...	(64×42,489 - 35,556)/63 = 42,599...
2	16	(4×30 − 16)/3 = 34,666...	(16×42 - 34,667)/15 = 42,489...
4	30	(4×39 - 30)/3 = 42
8	39

• MA oznacza dokładniejsze, LA oznacza mniej dokładne

Przykład

Na przykład funkcja Gaussa jest całkowana od 0 do 1, czyli funkcja błędu erf(1) ≈ 0,842700792949715. Tablica trójkątna jest obliczana wiersz po wierszu, a obliczenia są kończone, jeśli dwa ostatnie wpisy w ostatnim wierszu różnią się mniej niż 10 ⁻⁸ .

0,77174333 0,82526296 0,84310283 0,83836778 0,84273605 0,84271160 0,84161922 0,84270304 0,84270083 0,84270066 0,84243051 0,84270093 0,84270079 0,84270079 0,84270079

Wynik w prawym dolnym rogu trójkątnej tablicy odpowiada pokazanym cyfrom. Godne uwagi jest to, że wynik ten pochodzi z mniej dokładnych przybliżeń uzyskanych za pomocą reguły trapezu w pierwszej kolumnie trójkątnej tablicy.

Realizacja

Oto przykład komputerowej implementacji metody Romberga (w języku programowania C ):

 
 

     
    
       0     
       
    #include  <stdio.h>  #include  <math.h>  void  print_row  (  size_t  i  ,  double  *  R  )  {  printf  (  "R[%2zu] = "  ,  i  );  for  (  size_t jot  =  ;  j  <  =  ja  ;  ++  j  )  {  printf  (  "% f "  ,  R  [  j  ]);  } 
   













   printf  (  "  \n  "  );  }  /*  INPUT:  (*f) : wskaźnik funkcji do całkowania  a : dolna granica  b : górna granica  max_steps: maksymalna liczba kroków procedury  acc : wymagana dokładność  OUTPUT:  Rp[max_steps-1]: przybliżona wartość całki funkcji f dla x w [a,b] z dokładnością 'acc' i krokami 'max_steps'.  */  podwójny  romberg  (  podwójny  (  *  f  )(  podwójny  ),          

      
      0   0 
       double  a  ,  double  b  ,  size_t  max_steps  ,  double  acc  )  {  double  R1  [  max_steps  ],  R2  [  max_steps  ];  // buforuje  podwójnie  *  Rp  =  &  R1  [  ],  *  Rc  =  &  R2  [  ];  // Rp to poprzedni wiersz, Rc to bieżący wiersz  double  h  =  b  -  
   0     

   0 

            
        
       za  ;  //rozmiar kroku  Rp  [  ]  =  (  f  (  a  )  +  f  (  b  ))  *  h  *  0,5  ;  // pierwszy stopień trapezu  print_row  (  ,  Rp  );  for  (  size_t  i  =  1  ;  ja  <  max_steps  ;  ++  ja  )  {  h  /=  2.  ;  podwójnie    0
            
               
           
      
      0   do  =  ;  rozmiar_t  ep  =  1  <<  (  i  -1  );  //2^(n-1)  for  (  rozmiar_t jot  =  1  ;  jot  <  =  ep  ;  ++  j  )  {  do  +=  fa  (  za  +  (  2  *  j  -1  )  *  h  );  }  Rc  [  ]  =  h  *   0 

               
             
              c  +  0,5  *  Rp  [  ];  // R(i,0)  for  (  size_t  j  =  1  ;  j  <=  ja  ;  ++  j  )  {  double  n_k  =  pow  (  4  ,  j  );  Rc  [  j  ]  =  (  n_k  *  Rc  [  j  -1  ]  -  Rp  [  j  -1    
      

      
       

              
          
       ])  /  (  n_k  -1  );  // oblicz R(i,j)  }  // Wypisz i-ty wiersz R, R[i,i] jest jak dotąd najlepszym oszacowaniem  print_row  (  i  ,  Rc  );  if  (  i  >  1  &&  fabs  (  Rp  [  i  -1  ]  -  Rc  [  i  ])  <  acc  )  {  return  Rc  [  i  ];  } 

      
         
        
        
   
     
 // zamień Rn i Rc, ponieważ potrzebujemy tylko ostatniego wiersza  double  *  rt  =  Rp  ;  Rp  =  Rc  ;  Rc  =  rt  ;  }  zwróć  Rp  [  max_steps  -1  ];  // zwróć nasze najlepsze przypuszczenie  } 

Oto przykład komputerowej implementacji metody Romberga w języku programowania Javascript .

     /**  * WEJŚCIA  * func = całka, funkcja do całkowania  * a = dolna granica całkowania  * b = górna granica całkowania  * nmax = liczba partycji, n=2^nmax  * tol_ae = maksymalny dopuszczalny bezwzględny błąd przybliżony (powinien być >=0)  * tol_rae = maksymalny dopuszczalny bezwzględny względny błąd przybliżony (powinien być >=0)  * WYJŚCIA  * wartość_całki = oszacowana wartość całki  */  funkcja  auto_integrator_trap_romb_hnm  (  func  ,  a  ,  b  ,  nmax  ,    
       
      
  
       
      
  
    tol_ae  ,  tol_rae  )  {  if  (  typeof  a  !==  'number'  )  {  throw  new  TypeError  (  '<a> musi być liczbą'  );  }  if  (  typeof  b  !==  'number'  )  {  throw  new  TypeError  (  '<b> musi być liczbą'  );  }  jeśli  (  !  Liczba  .    
      
  
          0 
       isCałkowita  (  nmax  )  ||  nmax  <  1  )  {  throw  new  TypeError  (  '<nmax> musi być liczbą całkowitą większą lub równą jeden.'  );  }  if  ((  typeof  tol_ae  !==  'number'  )  ||  tol_ae  <  )  {  throw  new  TypeError  (  '<tole_ae> musi być liczbą większą lub równą zeru'  ); 
  
          0 
      
  
    
       
  
      
     }  if  ((  typeof  tol_rae  !==  'number'  )  ||  tol_rae  <=  )  {  throw  new  TypeError  (  '<tole_ae> musi być liczbą większą lub równą zeru'  );  }  var  h  =  b  -  a  ;  // zainicjuj macierz, w której przechowywane są wartości całki  var  Romb  =  [];  // wiersze  dla  (  var  i   0     
    
        0     
      0
    
   =  ;  i  <  nmax  +  1  ;  i  ++  )  {  Romb  .  pchnij  ([]);  dla  (  var  jot  =  ;  j  <  nmax  +  1  ;  j  ++  )  {  Romb  [  ja  ].  push  (  matematyka  .  duża liczba  (  ));  }  } 

  
  00      
     00

        // obliczanie wartości za pomocą 1-segmentowej reguły trapezów  Romb  [  ][  ]  =  0,5  *  h  *  (  func  (  a  )  +  func  (  b  ));  var  integ_val  =  Romb  [  ][  ];  for  (  var  i  =  1  ;  ja  <=  nmax  ;  ja  ++  )  { 
    
    
    
	    
       0
         
       // aktualizacja wartości o podwójną liczbę segmentów  // używając tylko wartości tam, gdzie trzeba je obliczyć  // Zobacz https://autarkaw.org/2009/02/28/an-performance-formula-for-an -automatyczny-całkujący-oparty-na-regule-trapezoidalnej/  h  =  h  /  2  ;  var  liczba całkowita  =  ;  dla  (  zmienna  jot  =  1  ;  jot  <=  2  **  ja  -  1  ;  jot  +=  2  )  {  zmienna  
    

    0  0  
    
    
       liczba całkowita  =  liczba całkowita  +  funkcja  (  a  +  j  *  h  )  }  liczba całkowita  [  i  ][  ]  =  0,5  *  liczba całkowita  [  i  -  1  ][  ]  +  liczba całkowita  *  h  ;  // Wykorzystanie metody Romberga do obliczenia następnej ekstrapolowalnej wartości  // Zobacz https://young.physics.ucsc.edu/115/romberg.pdf  dla  (  k  =  1  ;  k      
       
      
         <=  ja  ;  k  ++  )  {  var  addterm  =  Romb  [  i  ][  k  -  1  ]  -  Romb  [  i  -  1  ][  k  -  1  ]  addterm  =  addterm  /  (  4  **  k  -  1,0  )  Romb  [  i  ][  k  ]  =  Romb  [  ja 

      
         
      
          ][  k  -  1  ]  +  addterm  // Obliczanie bezwzględnego przybliżonego błędu  var  Ea  =  math  .  abs  (  Romb  [  i  ][  k  ]  -  Romb  [  i  ][  k  -  1  ])  // Obliczanie bezwzględnego względnego przybliżonego błędu  var  epsa  =  math  .  abs  (  Ea  /  Romb  [  i  ][   
			
      
        

      
          
         
      
    
  
   k  ])  *  100,0  ;  //Przypisanie ostatniej wartości zmiennej zwracanej  integ_val  =  Romb  [  i  ][  k  ];  // zwrócenie wartości, jeśli któraś z tolerancji jest spełniona  if  (  epsa  <  tol_rae  ||  Ea  <  tol_ae  )  {  return  integ_val  ;  }  }  } //   zwrócenie  ostatnio obliczonej wartości całki niezależnie od tego czy tolerancja jest spełniona czy nie 
   
 liczba_całkowa  ;  } 

•   Richardson, LF (1911), „Przybliżone rozwiązanie arytmetyczne według skończonych różnic problemów fizycznych obejmujących równania różniczkowe, z zastosowaniem do naprężeń w zaporze murowanej”, Philosophical Transactions of the Royal Society A , 210 (459–470): 307 –357, doi : 10.1098/rsta.1911.0009 , JSTOR 90994
• Romberg, W. (1955), "Vereinfachte numerische Integration", Det Kongelige Norske Videnskabers Selskab Forhandlinger , Trondheim, 28 (7): 30–36
• Thacher Jr., Henry C. (lipiec 1964), „Uwaga na temat algorytmu 60: integracja Romberga” , Komunikacja ACM , 7 (7): 420–421, doi : 10,1145 / 364520,364542
• Bauer, Floryda; Rutishauser, H.; Stiefel, E. (1963), Metropolis, Karolina Północna; i in. (red.), „Nowe aspekty kwadratury numerycznej”, Experimental Arithmetic, high-speed computing and matematyc, Proceedings of Symposia in Applied Mathematics , AMS (15): 199–218
• Bulirsch, Roland; Stoer, Josef (1967), „Handbook Series Numerical Integration. Numeryczna kwadratura przez ekstrapolację” , Numerische Mathematik , 9 : 271–278, doi : 10.1007 / bf02162420
•   Mysovskikh, IP (2002) [1994], „Metoda Romberga” , w Hazewinkel, Michiel (red.), Encyclopedia of Mathematics , Springer-Verlag , ISBN 1-4020-0609-8
•   Prasa, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), „Sekcja 4.3. Integracja Romberga” , Przepisy numeryczne: The Art of Scientific Computing (wyd. 3), Nowy Jork: Cambridge University Press, ISBN 978-0-521-88068-8

Linki zewnętrzne

• ROMBINT – kod dla MATLAB (autor: Martin Kacenak)
• Bezpłatne narzędzie do integracji online wykorzystujące metody Romberg, Fox-Romberg, Gauss-Legendre i inne metody numeryczne
• Implementacja SciPy metody Romberga
• Romberg.jl - Implementacja Julii $punktów$ obsługa dowolnych a nie tylko