Metoda linearyzacji lokalnej

W analizie numerycznej metoda linearyzacji lokalnej (LL) jest ogólną strategią projektowania integratorów numerycznych dla równań różniczkowych w oparciu o lokalną (odcinkową) linearyzację danego równania w kolejnych przedziałach czasu. Integratory numeryczne są następnie iteracyjnie definiowane jako rozwiązanie otrzymanego odcinkowo równania liniowego na końcu każdego kolejnego przedziału. Metoda LL została opracowana dla różnych równań, takich jak zwykłe , opóźnione , losowe i stochastyczne równania różniczkowe. Integratory LL są kluczowym elementem implementacji metod wnioskowania do estymacji nieznanych parametrów i nieobserwowalnych zmiennych równań różniczkowych na podstawie szeregów czasowych (potencjalnie zaszumionych) obserwacji. Schematy LL są idealne do radzenia sobie ze złożonymi modelami w różnych dziedzinach, takich jak neuronauka , finanse , gospodarka leśna , inżynieria sterowania , statystyka matematyczna itp.

Tło

Równania różniczkowe stały się ważnym narzędziem matematycznym do opisu ewolucji w czasie wielu zjawisk, np. rotacji planet wokół Słońca, dynamiki cen aktywów na rynku, pożaru neuronów, rozprzestrzeniania się epidemii itp. Jednakże, ponieważ dokładne rozwiązania tych równań są zwykle nieznane, konieczne są numeryczne przybliżenia do nich uzyskane za pomocą integratorów numerycznych. Obecnie wiele zastosowań w inżynierii i naukach stosowanych ukierunkowanych na badania dynamiczne wymaga opracowania wydajnych integratorów numerycznych, które w jak największym stopniu zachowują dynamikę tych równań. Kierując się tą główną motywacją, opracowano integratory Local Linearization.

Metoda linearyzacji lokalnej wysokiego rzędu

Metoda linearyzacji lokalnej wysokiego rzędu (HOLL) jest uogólnieniem metody linearyzacji lokalnej ukierunkowanej na uzyskanie integratorów wysokiego rzędu dla równań różniczkowych, które zachowują stabilność i dynamikę równań liniowych. Integratory uzyskuje się przez podzielenie, w kolejnych przedziałach czasu, rozwiązania x pierwotnego równania na dwie części: rozwiązanie z lokalnie zlinearyzowanego równania plus przybliżenie wysokiego rzędu reszty ${\ Displaystyle \ mathbf {r} = \ mathbf {x} - \ mathbf {z}}$ .

Lokalny schemat linearyzacji

Schemat linearyzacji lokalnej (LL) jest ostatecznym algorytmem rekurencyjnym , który umożliwia numeryczną implementację dyskretyzacji wyprowadzonej z metody LL lub HOLL dla klasy równań różniczkowych.

Metody LL dla ODE

Rozważ d -wymiarowe równanie różniczkowe zwyczajne (ODE)

${\ Displaystyle {\ Frac {d \ mathbf {x} \ lewo (t \ prawo)} {dt}}=\mathbf {f} \left(t,\mathbf {x} \left(t\right)\right),\qquad t\in \left[t_{0},T\right],\ qquad \qquad \qquad \qquad (4.1)}$

z warunkiem początkowym ${\ Displaystyle \ mathbf {x} (t_ {0}) = \ mathbf {x} _ {0}}$ , gdzie ${\ Displaystyle \ mathbf {f}}$ jest funkcją różniczkowalną .

Niech ${\ Displaystyle \ lewo (t \ prawo) _ {h} = \ {t_ {n}: n = 0, ..., N \}} być dyskretyzacją czasową przedziału$ czasu ${ \displaystyle [t_ {0}, T]}$ z maksymalnym stopniem h takim, że ${\ displaystyle t_ {n}<t_ {n + 1}}$ i ${\ Displaystyle h_ {n} = t_ {n + 1} -t_ {n} \ równoważnik h}$ . Po lokalnej linearyzacji równania (4.1) w kroku czasowym wariacja stałych równań daje ${\ displaystyle t_ {n}}$

${\ Displaystyle \ mathbf {x} (t_ {n} + h) = \ mathbf {x} (t_ {n}) + \ mathbf {\ fi} (t_ {n}, \ mathbf {x} (t_ {n} });h)+\mathbf {r} (t_{n},\mathbf {x} (t_{n});h),}$

Gdzie

${\ Displaystyle \ mathbf {\ fi} (t_ {n}, \ mathbf {z} _ {n}; h) = \ int \ limity _ {0} ^ {h} e ^ {\ mathbf {f} _ { \mathbf {x} }(t_{n},\mathbf {z} _{n})(hs)}(\mathbf {f} (t_{n},\mathbf {z} _{n})+\ mathbf {f} _{t}(t_{n},\mathbf {z} _{n})s)\,ds\qquad }$

wynika z przybliżenia liniowego, oraz

${\ Displaystyle \ mathbf {r} (t_ {n}, \ mathbf {z} _ {n}; h) = \ int \ ograniczenia _ {0} ^ {h} e ^ {\ mathbf {f} _ {\ mathbf {x} }(t_{n},\mathbf {z} _{n})(hs)}\mathbf {g} _{n}(s,\mathbf {x} (t_{n}+s) )\,ds,\qquad \qquad \qquad (4.2)}$

jest resztą z liniowego przybliżenia. Tutaj ${\ Displaystyle \ mathbf {f} _ {\ mathbf {x}}}$$i$ oznaczają f względem zmiennych x i t , odpowiednio, i ${\ Displaystyle \ mathbf {g} _ {n} (s, \ mathbf {u}) = \ mathbf {f} (s, \ mathbf {u}) - \ mathbf {f} _ {\ mathbf {x}} (t_{n},\mathbf {z} _{n})\mathbf {u} -\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s- t_{n})-\mathbf {f} (t_{n},\mathbf {z} _{n})+\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf { z} _{n})\mathbf {z} _{n}.}$

Lokalna dyskretyzacja liniowa

Dla dyskretyzacji czasu ${\ Displaystyle \ lewo (t \ prawej) _ {h}}$ , lokalna dyskretyzacja liniowa ODE (4.1) w każdym punkcie ${\ displaystyle t_ {n+1}\in \left(t\right)_{h}}$ jest zdefiniowane przez wyrażenie rekurencyjne

${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} (t_ {n}, \ mathbf {z} _ {n}; h_{n}),\qquad {\text{z }}\quad \mathbf {z} _{0}=\mathbf {x} _{0}.\qquad \qquad \qquad \qquad (4.3)}$

Lokalna dyskretyzacja liniowa (4.3) jest zbieżna z rzędem 2 do rozwiązania nieliniowych ODE, ale pasuje do rozwiązania liniowych ODE. Rekurencja (4.3) jest również znana jako wykładnicza dyskretyzacja Eulera.

Lokalne dyskretyzacje liniowe wysokiego rzędu

Dla dyskretyzacji czasu ${\ Displaystyle (t) _ {h},}$ lokalnej dyskretyzacji liniowej wysokiego rzędu (HOLL) ODE (4.1) w każdym punkcie ${ \displaystyle t_{n+1}\in (t)_{h}}$ jest zdefiniowane przez wyrażenie rekurencyjne

${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} (t_ {n}, \ mathbf {z} _ {n}; h_ {n })+ {\widetilde {\mathbf {r}}}(t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{z }}\quad \mathbf { z} _{0}=\mathbf {x} _{0},\qquad \qquad \qquad (4.4)}$

gdzie ${\ Displaystyle {\ tylda {r}}}$ jest rzędem przybliżenia do reszty r ${\ displaystyle \ alpha}$ > 2 ${\ Displaystyle (tj. \ lewo \ vert \ mathbf {r} (t_ {n}, \ mathbf {z} _ {n}; h) - {\ widetilde {\ mathbf {r}}} (t_ {n} ,\mathbf {z} _ {n};h)\right\vert \propto h ^{\alpha +1}).}$ Dyskretyzacja HOLL (4.4) zbiega się z rzędem ${\ displaystyle \ alpha}$ do rozwiązania nieliniowych ODE, ale pasuje do rozwiązania liniowych ODE.

Dyskretyzacje HOLL-a można wyprowadzić na dwa sposoby: 1) (na podstawie kwadratur) przez aproksymację całkowej reprezentacji (4.2) r ; oraz 2) (oparte na integratorze) przy użyciu integratora numerycznego dla reprezentacji różniczkowej r określonej przez

${\ Displaystyle {\ Frac {d \ mathbf {r} (t )}{dt}}=\mathbf {q} (t_{n},\mathbf {z} _{n};t\mathbf {,\mathbf {r}} (t)\mathbf {)} ,\qquad {\text{z }}\qquad \mathbf {r} (t_{n})=\mathbf {0,} \qquad \qquad \qquad (4.5)}$

dla wszystkich ${\ Displaystyle t \ w \ lbrack t_ {k}, t_ {k + 1}]} ,$ gdzie

${\ Displaystyle \ mathbf {q} (t_ {n}, \ mathbf {z} _ {n}; s \ mathbf {, \ xi}) = \ mathbf {f} (s, \ mathbf {z} _ {n }+\mathbf {\phi} \left(t_{n},\mathbf {z} _{n};s-t_{n}\right)+\mathbf {\xi} )-\mathbf {f} _ {\mathbf {x}}(t_{n},\mathbf {z} _{n})\mathbf {\phi} (t_{n},\mathbf {z} _{n};s-t_{n })-\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\mathbf {z} _ {n}).}$

Dyskretyzacje HOLL to na przykład:

• Lokalnie zlinearyzowana dyskretyzacja Runge Kutta

${\ Displaystyle \ qquad \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} (t_ {n},\mathbf {z} _{n};h_{n})+h_{n}\suma _{j=1}^{s}b_{j}\mathbf {k} _{j}, \quad {\text{ z }}\quad \mathbf {k} _{i}=\mathbf {q} (t_{n},\mathbf {z} _{n};{\text{ }}t_{ n}+c_{i}h_{n}\mathbf {,} \mathbf {} h_{n}\suma _{j=1}^{i-1}a_{ij}\mathbf {k} _{j }),}$

który otrzymuje się przez rozwiązanie (4.5) za pomocą s-etapowego jawnego schematu Runge-Kutty (RK) ze współczynnikami ${\ Displaystyle \ mathbf {c} =\left[c_{i}\right],\mathbf {A} =\left[a_{ij}\right]\quad i\quad \mathbf {b} =\left[b_{j} \prawo]}$ .

• Lokalna liniowa dyskretyzacja Taylora

$${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} (t_ {n}, \ mathbf {z} _ {n}; h_ {n })+\int _{0}^{h_{n}}e^{(h_{n}-s)\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {z} _{n}\right)}\sum _{j=2}^{p}{\frac {\mathbf {c} _{n,j}}{j!}}s^{j}\ ,ds,{\text{ z }}\mathbf {c} _{n,j}=\left({\frac {d^{j+1}\mathbf {x} (t)}{dt^{j +1}}}-\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n}){\frac {d^{j}\mathbf {x} ( t)}{dt^{j}}}\right)\mid _{t=\mathbf {z} _{n}},}$$

co wynika z przybliżenia w (4.2) przez jego okrojone rozwinięcie Taylora rzędu p . ${\ displaystyle \ mathbf {g} _ {n}}$

• Dyskretyzacja propagacji wykładniczej typu wieloetapowego

${\ textstyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \mathbf {\phi} (t_{n},\mathbf {z} _{n};h)+h\sum _{j=0}^{p-1}\gamma _{j}\nabla ^{ j}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad z\quad \gamma _{j}=(-1)^{j}\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n})} \left({\begin{tablica}{c}-\theta \\j\end{tablica}}\right)d\theta ,}$

sol $_ {n}}$${\ displaystyle t_ {n} \ ldots, t_ {np + 1}}$ w (4.2) wielomianem stopnia p na , gdzie ${\ Displaystyle \ nabla ^ {j} \ mathbf {g} _ {n} (t_ {m}, \mathbf {z} _{m})}$ oznacza j -ty wsteczna różnica sol $\ Displaystyle \ mathbf {g} _ {n} (t_ {m}, \ mathbf {z} _ {m})}$ .

• Dyskretyzacja typu Runge Kutta z propagacją wykładniczą

${\ textstyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ phi } (t_{n},\mathbf {z} _{n};h)+h\suma _{j=0}^{p-1}\gamma _{j,p}\nabla ^{j} \mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad {\text{ with }}\quad \gamma _{j,p}=\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n})}\left ({\begin{array}{c}\theta p\\j\end{array}}\right)d\theta ,}$

sol $_ {n}}$${\ styl wyświetlania t_{n},\ldots ,t_{n}+(p-1)h/p}$ w (4.2) przez wielomian stopnia p na ,

• Zliniowana wykładnicza dyskretyzacja Adamsa

${\textstyle \mathbf {z} _ {n+1} = \ mathbf {z} _ {n} + \ mathbf {\ phi} (t_ {n}, \ mathbf {z} _ {n}; h) + h\sum _{j=1}^{p-1}\sum _{l=1}^{j}{\frac {\gamma _{j+1}}{l}}\nabla ^{l} \mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad {\text{ z }}\quad \gamma _{j+1}=(-1) ^{j+1}\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }\left(t_{n},\ mathbf {z} _{n}\right)}\theta \left({\begin{tablica}{c}-\theta \\j\end{tablica}}\right)d\theta ,}$

sol ${\ displaystyle \ mathbf {g} _ {n}}$ w (4.2) przez wielomian hermite'a stopnia p na ${n },\ldots ,t_{n-p+1}}$ .

Lokalne schematy linearyzacji

$z$ numeryczna implementacja dyskretyzacji LL (lub HOLL) $Displaystyle \ mathbf {z} _ {n}}$${\ displaystyle {\ widetilde {\ phi}} _ {j}}$ obejmuje przybliżenia do całek postaci ${\ Displaystyle \ phi _ {j}}$

${\ Displaystyle \ phi _ {j} (\ mathbf {A}, h) = \int \limits _{0}^{h}e^{(hs)\mathbf {A}}s^{j-1}\,ds,\qquad j=1,2\ldots ,}$

gdzie A jest macierzą d × d . Każda numeryczna implementacja $dowolnej$ (lub HOLL) kolejności jest ogólnie nazywana Linearyzacją lokalną y $\ displaystyle \ mathbf {z} _ {n}$ schemat .

Obliczanie całek z macierzą wykładniczą

Spośród wielu algorytmów do obliczania całek $są$ te oparte na racjonalnych przybliżeniach podprzestrzeni Padé i Kryłowa dla macierzy wykładniczej W tym celu kluczową rolę odgrywa ekspresja

${\ Displaystyle \ suma \ nolimits _ {i = 1} ^ {l} \ phi _ {i} (\ mathbf {A} ,h)\mathbf {a} _{i}=\mathbf {L} e^{h\mathbf {H}}\mathbf {r} ,}$

gdzie są d -wymiarowymi wektorami, $\ Displaystyle \ mathbf {a} _ {i}}$

${\ Displaystyle \ mathbf {H} = {\ rozpocząć {bmatrix} \ mathbf {A} & \ mathbf {v} _ {l} & \ mathbf {v} _ {l-1} & \ cdots & \ mathbf {v } _{1}\\\mathbf {0} &\mathbf {0} &1&\cdots &0\\\mathbf {0} &\mathbf {0} &0&\ddots &0\\\vdots &\vdots &\vdots & \ddots &1\\\mathbf {0} &\mathbf {0} &0&\cdots &0\end{bmatrix}}\in \mathbb {R} ^{(d+l)\times (d+l)},}$

${\ Displaystyle \ mathbf {L} = [\ mathbf {ja} \ quad \ mathbf {0} _ {d \ razy l}]}$ , ${\ Displaystyle \ mathbf {r} = [\ mathbf {0} _ {1 \ razy (d + l-1)} \ quad 1] ^ {\ intercal},}$$mathbf$${a} _ {i} (i-1)!} będąc$ d -wymiarową macierzą tożsamości.

P ${\ Displaystyle \ mathbf {P} _ {p, q} (2 ^ {- k} \ mathbf {H} h)}$ ( p ; q ) - Padé przybliżenie mi ${\ Displaystyle e ^ {2 ^ {- k} \ mathbf {H} h}}$ i k jest najmniejszą liczbą naturalną taką, ${\ Displaystyle | 2 ^ {- k} \ mathbf {H} h | \ równoważnik {\ Frac {1} {2}}, wtedy$

${\ Displaystyle \ lewo \ vert \ suma \ nolimits _ {i = 1} ^ {l} \ phi _ {i} (\ mathbf {A}, h) \ mathbf {a} _ {i} - \ mathbf {L } \left(\mathbf {\mathbf {P}} _{p,q}(2^{-k}\mathbf {H} h)\right)^{2^{k}}\mathbf {r} \ prawo\vert \varpropto h^{p+q+1}.}$

k ${\ mathbf {k}} _ {m, k} ^ {p, q} (h, \ mathbf {H} \ mathbf {r} )}$ oznacza przybliżenie ( m ; p ; q ; k ) Krylov-Padé a następnie mi $h \ mathbf {H}} \ mathbf {r}}$

${\ Displaystyle \ lewo \ vert \ suma \ nolimits _ {i = 1} ^ {l} \ phi _ {i} (\ mathbf {A}, h) \ mathbf {a} _ {i} - \ mathbf {L \mathbf {k} } _{m,k}^{p,q}(h,\mathbf {H} ,\mathbf {r} )\right\vert \varpropto h^{\min({m,p+ q+1})},}$

gdzie ${\ displaystyle m \ równoważnik d}$ jest wymiarem podprzestrzeni Kryłowa.

Zamówienie-2 schematy LL

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2 ^ {k_ {n}}} \ mathbf {r}}$${\ Displaystyle \ qquad \ qquad (4,6)}$

gdzie macierze L i r są zdefiniowane jako ${\ Displaystyle \ mathbf {M} _ {n}}$

${\ Displaystyle \ mathbf {M} _ {n} = {\ rozpocząć {bmatrix} \ mathbf {f} _ {\ mathbf {x}} (t_ {n}, \ mathbf {y} _ {n}) i \ mathbf {f} _{t}(t_{n},\mathbf {y} _{n})&\mathbf {f} (t_{n},\mathbf {y} _{n})\\0&0&1\ \0&0&0\end{bmatrix}}\w \mathbb {R} ^{(d+2)\times (d+2)},}$

${\ Displaystyle \ mathbf {L} = \ lewo [{\ rozpocząć {tablica} {ll} \ mathbf {I} & \ mathbf {0} _ {d \ razy 2} \ koniec { tablica}} \ prawej]}$ i ${\ Displaystyle \ mathbf {r} ^ {\ intercal} = \ lewo [{\ rozpocząć {tablica} {ll} \ mathbf { 0} _ {1 \ razy (d + 1)} i 1 \ koniec {tablica}} \ prawej]}$ z ${\ displaystyle p + q> 1}$ . Dla dużych systemów ODE

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _{n}+\mathbf {L\mathbf {k}} _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{ n},\mathbf {r} )\mathbf {,} \qquad {\text{z }}\qquad m_{n}>2.}$

Zamówienie-3 schematy LL-Taylor

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf { y} _{n}+\mathbf {L} _{1}(\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {T} _{n}h_{n })) ^ {2 ^ {k_ {n}}} \ mathbf {r} _ {1} \ mathbf {}} ($$\ Displaystyle \ qquad \ qquad (4,7)}$

gdzie dla autonomicznych ODE macierze ${\ Displaystyle \ mathbf {T} _ {n}, \ mathbf {L} _ {1}}$ i ${\ Displaystyle \ mathbf {r} _ {1}}$ są określone jako

${\ Displaystyle \ mathbf {T} _ {n} = \ lewo [{\ rozpocząć {tablica} {cccc} \ mathbf {f} _ {\ mathbf {x}} (\ mathbf {y} _ {n}) & (\mathbf {I} \otimes \mathbf {f} ^{\intercal}(\mathbf {y} _{n}))\mathbf {f} _{\mathbf {xx}}(\mathbf {y} _ {n})\mathbf {f} (\mathbf {y} _{n})&\mathbf {0} &\mathbf {f} (\mathbf {y} _{n})\\0&0&0&0\\0&0&0&1\ \0&0&0&0\end{array}}\right]\in \mathbb {R} ^{(d+3)\times (d+3)},}$

${\ Displaystyle \ mathbf {L} _ {1} = \ lewo [{\ rozpocząć {tablica} {ll }\mathbf {I} &\mathbf {0} _{d\times 3}\end{array}}\right]\quad i\quad \mathbf {r} _{1}^{\intercal }=\left [{\begin{array}{ll}\mathbf {0} _{1\times (d+2)}&1\end{array}}\right]}$ . Tutaj, ${\ Displaystyle \ mathbf {f} _ {\ mathbf {xx}}}$ oznacza drugą pochodną f względem x i p + q > 2 . Dla dużych systemów ODE

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _{n}+\mathbf {L\mathbf {k}} _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {T} _{ n},\mathbf {r} )\mathbf {,} \qquad {\text{z }}\qquad m_{n}>3.}$

Zamówienie-4 schematy LL-RK

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n }+\mathbf {u} _{4}+{\frac {h_{n}}{6}}(2\mathbf {k} _{2}+2\mathbf {k} _{3}+\mathbf {k} _ {4}), \ quad}$${\ Displaystyle \ qquad \ qquad (4,8)}$

Gdzie

${\ Displaystyle \ mathbf {u} _ {j} = \ mathbf {L} (\ mathbf {P} _{p,q}(2^{-\kappa _{j}}\mathbf {M} _{n}c_{j}h_{n}))^{2^{\kappa_{j}}} \mathbf {r} }$

I

$\ Displaystyle \ mathbf {k} _ {j} = \ mathbf {f} \ lewo (t_ {n} + c_ {j} h_ {n}, \ mathbf {y } _{n}+\mathbf {u} _{j}+c_{j}h_{n}\mathbf {k} _{j-1}\right)-\mathbf {f} \left(t_{n },\mathbf {y} _{n}\right)-\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {y} _{n}\right)\mathbf {u} _{j}\ -\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right)c_{j}h_{n},}$

z ${\ Displaystyle \ mathbf {k} _ {1} \ równoważnik \ mathbf {0}, c = \ lewo [{\ rozpocząć {tablica} cccc} 0& {\frac {1}{2}}&{\frac {1}{2}}&1\end{array}}\right],}$ i p + q > 3 . W przypadku dużych systemów $przez$ wektor powyższym schemacie jest zastępowany $\ Displaystyle \ mathbf {u} _ {j} = \ mathbf {L \ mathbf {k}} _ {m_ {j}, k_ {j}} ^ {p, q} (c_ {j} h_ {n}, \ mathbf {M} _ {n}, \ mathbf {r})}$ z ${\ Displaystyle m_ {j}> 4.}$

Lokalnie zlinearyzowany schemat Runge-Kutty Dormanda i Prince'a

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n} + \ mathbf {u} _ {s} + h_ {n} \ suma _ {j = 1} ^ {s }b_{j}\mathbf {k} _{j}\qquad {\text{i}}\qquad {\widehat {\mathbf {y}}}_{n+1}=\mathbf {y} _{ n}+\mathbf {u} _{s}+h_{n}\suma _{j=1}^{s}{\widehat {b}}_{j}\mathbf {k} _{j}, \ quad }$${\ Displaystyle \ qquad \ qquad (4,9)}$

gdzie s = 7 to liczba stopni,

$\ Displaystyle \ mathbf {k} _ {j} = \ mathbf {f (} t_ {n} + c_ {j} h_ {n} ,\mathbf {y} _{n}+\mathbf {u} _{j}+h_{n}\suma _{i=1}^{s-1}a_{j,i}\mathbf {k} _{i})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{\mathbf {x} }\left(t_{ n},\mathbf {y} _{n}\right)\mathbf {u} _{j}\ -\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{ n}\right)c_{j}h_{n},}$

k $jot$$ja },b_{j},{\widehat {b}}_{j}\quad i\quad c_{j}}$ , to współczynniki Runge-Kutty Dormanda i Prince'a oraz p + q > 4. Wektor ${ \ displaystyle \ mathbf {u} _ {j}}$ w powyższym schemacie jest obliczana przez przybliżenie Padé lub Krylor-Padé odpowiednio dla małych lub dużych systemów ODE.

Stabilność i dynamika

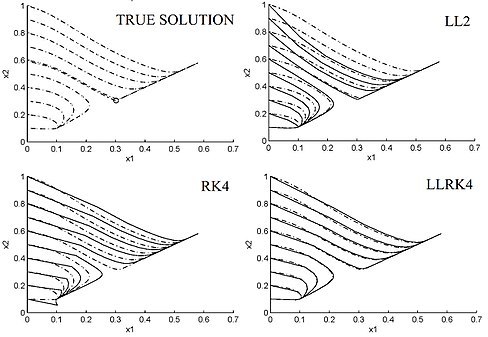
Rys. 1 Portret fazowy (linia przerywana) i przybliżony portret fazowy (linia ciągła) nieliniowego ODE (4.10)-(4.11) obliczonego według schematu LL rzędu 2 (4.2), klasycznego schematu Rugena-Kutty rzędu 4 RK 4 i schematy rzędu 4 LLRK 4 (4.8) z wielkością kroku h=1/2 i p=q=6.

Z założenia dyskretyzacje LL i HOLL dziedziczą stabilność i dynamikę liniowych ODE, ale ogólnie nie dotyczy to schematów LL. Z ${\ Displaystyle p \ równoważnik q \ równoważnik p + 2}$ , schematy LL (4,6) - (4,9) są A -stabilne . Przy q = p + 1 lub q = p + 2, schematy LL (4.6)–(4.9) są również L -stabilne . Dla liniowych ODE schematy LL (4.6)-(4.9) są zbieżne z rzędem p + q . Ponadto, przy p = q = 6 i $=$ , wszystkie opisane powyżej schematy LL dają „dokładne obliczenie” (z dokładnością do arytmetyki zmiennoprzecinkowej liniowej ODE na obecnych komputerach osobistych. Obejmuje to sztywne i wysoce oscylacyjne równania liniowe. Ponadto schematy LL (4.6)-(4.9) są regularne dla liniowych ODE i dziedziczą symplektyczną strukturę hamiltonowskich oscylatorów harmonicznych . Te schematy LL zachowują również linearyzację i wykazują lepszą reprodukcję stabilnych i niestabilnych rozmaitości wokół hiperbolicznych punktów równowagi i orbit okresowych niż inne schematy numeryczne o tym samym rozmiarze kroku. Na przykład rysunek 1 przedstawia portret fazowy ODE

${\ Displaystyle {\ rozpocząć {wyrównane} i {\ Frac {dx_ {1}} {dt}} = -2x_ {1} + x_ {2} + 1- \ mu f (x_ {1}, \ lambda) \ qquad \qquad (4.10)\\[6pt]&{\frac {dx_{2}}{dt}}=x_{1}-2x_{2}+1-\mu f(x_{2},\lambda ) \qquad \qquad \quad (4.11)\end{wyrównane}}}$

z ${\ Displaystyle f (u, \ lambda) = u (1 + u + \ lambda u ^ {2}) ^ {- 1}}$ , ${\ Displaystyle \ mu = 15}$ i ${\ Displaystyle \ lambda = 57}$ i jego przybliżenie różnymi schematami. Układ ten ma dwa stabilne punkty stacjonarne i jeden niestabilny punkt stacjonarny w regionie ${\ Displaystyle 0 \ równoważnik x_ {1}, x_ {2} \ równoważnik 1}$ .

Metody LL dla DDE

Rozważ d -wymiarowe równanie różniczkowe opóźnienia (DDE)

${\ Displaystyle {\ Frac {d \ mathbf {x} (t)}} {dt}} = \ mathbf {f} (t, \ mathbf {x} (t), \ mathbf {x} _ {t} (- \tau _{1}),\ldots ,\mathbf {x} _{t}(-\tau _{m})),\qquad t\in [t_{0},T],\qquad \qquad ( 5.1)}$

z m stałymi opóźnieniami ${\ Displaystyle \ tau _ {i}> 0}$ i warunek początkowy ${\ Displaystyle \ mathbf {x} _ {t_ {0}} (s) =\ mathbf {\ varphi} (s)}$ dla wszystkich ${\ Displaystyle s \ in [- \ tau, 0],}$ gdzie f jest funkcją różniczkowalną, ${\ Displaystyle \ mathbf {x} _ {t}: [- \ tau, 0] \ longrightarrow \ mathbb {R} ^ {d}} jest$ funkcją segmentu zdefiniowaną jako

${\ Displaystyle \ mathbf {x} _ {t} (s): = \ mathbf {x} (t ​​+ s), {\text{}}s\w [-\tau ,0],}$

dla wszystkich ${\ Displaystyle t \ w [t_ {0}, T] \ mathbf {\ varphi}: [- \ tau, 0] \ longrightarrow \mathbb {R} ^{d}}$ jest daną funkcją, a ${\ Displaystyle \ tau = \ max \ lewo \ {\ tau _ {1}, \ ldots, \ tau _ {m} \ prawo \}.}$

Lokalna dyskretyzacja liniowa

Dla dyskretyzacji czasu ${\ Displaystyle (t) _ {h}}$ , lokalna liniowa dyskretyzacja DDE (5.1) w każdym punkcie ${\ displaystyle t_ {n + 1 }\in (t)_{h}}$ jest zdefiniowane przez wyrażenie rekurencyjne

${\ Displaystyle \ mathbf {z} _ {n + 1 }=\mathbf {z} _{n}+\Phi (t_{n},\mathbf {z} _{n},h_{n};{\widetilde {\mathbf {z}}}_{t_{ n}}^{1},\ldots,{\widetilde {\mathbf {z}}}_{t_{n}}^{m}),\qquad \qquad (5.2)}$

Gdzie

${\ Displaystyle \ Phi (t_ {n}, \ mathbf {z} _ {n}, h_ {n}; {\ widetilde {\ mathbf {z}}} _ {t_ {n}} ^ {1}, \ ldots ,{\widetilde {\mathbf {z}}}_{t_{n}}^{m})=\int \limits _{0}^{h_{n}}e^{\mathbf {A} _ {n}(h_{n}-u)}\left[\sum \limits _{i=1}^{m}\mathbf {B} _{n}^{i}({\widetilde {\mathbf { z} }}_{t_{n}}^{i}(u-\tau _{i})-{\widetilde {\mathbf {z}}}_{t_{n}}^{i}(- \tau _{i}})+\mathbf {d} _{n}\right]\,du+\int \limits_{0}^{h_{n}}\int \limits _{0}^{u }e^{\mathbf {A} _{n}(h_{n}-u)}\mathbf {c} _{n}\,dr\,du}$

${\ Displaystyle {\ widetilde {\ mathbf {z}}} _ {t_ {n}} ^ {i}: \ lewo [- \ tau _ {i },0\right]\longrightarrow \mathbb {R} ^{d}}$ to funkcja segmentu zdefiniowana jako

${\ Displaystyle {\ widetilde {\ mathbf {z}}} _ {t_ {n}} ^{i}(s):={\widetilde {\mathbf {z}}}^{i}(t_{n}+s),{\text{}}s\w [-\tau _{i} ,0],}$

i $} ^ {d}}$${\ Displaystyle {\ widetilde {\ mathbf {z}}} ^ {i}: \ lewo [t_ {n} - \ tau _ {i }, t_ {n$$t$ przybliżeniem dla wszystkich ${\ Displaystyle t \ in \ lbrack t_ {n} - \ tau _ {i}, t_ {n}]}$ takie, że ${\ Displaystyle {\ widetilde {\ mathbf {z}}} ^ {i} (t_ {n}) = \ mathbf {z} _ {n}.} Tutaj$ ,

${\ Displaystyle \ mathbf {A} _ {n} = \ mathbf {f} _ {x} (t_ {n}, \ mathbf {z} _ {n}, {\ widetilde {\ mathbf {z}}} _ {t_{n}}^{1}(-\tau _{1}),\ldots ,{\widetilde {\mathbf {z}}}_{t_{n}}^{m}(-\tau _ {d})),{\text{ }}\mathbf {B} _{n}^{i}=\mathbf {f} _{x_{t}(-\tau _{i})}(t_{ n},\mathbf {z} _{n},{\widetilde {\mathbf {z}}}_{t_{n}}^{1}(-\tau _{1}),\ldots,{\ szeroka tylda {\mathbf {z}}}_ {t_ {n}}^{m}(-\tau _{d})}}$

są macierzami stałymi i

${\ Displaystyle \ mathbf {c} _ {n} = \ mathbf {f} _ {t} (t_ {n}, \ mathbf { z} _{n},{\widetilde {\mathbf {z}}}_{t_{n}}^{1}(-\tau _{1}),\ldots,{\widetilde {\mathbf {z } }}_{t_{n}}^{m}(-\tau _{d})){\text{i }}\mathbf {d} _{n}=\mathbf {f(} t_{n },\mathbf {z} _{n},{\widetilde {\mathbf {z}}}_{t_{n}}^{1}(-\tau _{1}),\ldots,{\widetilde {\mathbf {z}}}_{t_{n}}^{m}(-\tau _{d}))}$

są stałymi wektorami. ${\ Displaystyle \ mathbf {f} _ {t}, \ mathbf {f} _ {x} \ quad i \ quad \ mathbf {f} _ { x_ {t} (- \ tau _ {i})}}$ oznaczamy odpowiednio pochodne cząstkowe f względem zmiennych t i x oraz ${\ Displaystyle \ mathbf {x} _ {t}(-\tau _{i})}$ . Lokalna dyskretyzacja liniowa (5.2) zbiega się do rozwiązania (5.1) z rzędem ${\ Displaystyle \ alpha = \ min \ {2, r \},}$ jeśli ${ \ Displaystyle {\ widetilde {\ mathbf {z}}} _ {t_ {n}} ^ {i}}$ przybliża ${\ Displaystyle \ mathbf {z} _ {t_ {n}} ^ {i}}$ z rzędem ${\ Displaystyle r \ quad (tj. \ lewo \ vert \ mathbf {z} _ {t_ {n}} ^ {i} \ mathbf {(} u- \ tau _ {i} \ mathbf {) } -{\widetilde {\mathbf {z}}}_{t_{n}}^{i}\mathbf {(} u-\tau _{i}\mathbf {)} \right\vert \propto h_{ n}^{r}}$ dla wszystkich ${\ Displaystyle u \ w \ lbrack 0, h_ {n}]}}$ .

Lokalne schematy linearyzacji

Ryc. 2 Przybliżone ścieżki Marchuk et al. (1991) przeciwwirusowy model immunologiczny opisany sztywnym systemem dziesięciowymiarowych nieliniowych DDE z pięcioma opóźnieniami czasowymi: górny, ciągły schemat Runge-Kutty (2,3) ; dół, schemat LL (5.3). Wielkość kroku h = 0,01 stała, a p = q = 6.

W zależności od przybliżeń $phi$ ϕ $} }$$\ Displaystyle \ mathbf$ można zdefiniować różne schematy Linearyzacji Lokalnych. $linearyzacji$ numeryczna implementacja $lokalnej$ liniowej jest nazywana lokalnym schematem

Schematy wielomianowe rzędu 2 LL

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2 ^ {k_ {n}}} \ mathbf {r} \ quad}$${\ Displaystyle \ qquad (5.3)}$

gdzie macierze są zdefiniowane jako ${\ Displaystyle \ mathbf {M} _ {n}, \ mathbf {L}}$ i ${\ Displaystyle \ mathbf {r}}$

${\ Displaystyle \ mathbf {M} _ {n} = {\ rozpocząć {bmatrix} \ mathbf {A} _ {n} & \ mathbf {c} _ {n} + \ suma \ limity _ {i = 1} ^ {m}\mathbf {B} _{n}^{i}\mathbf {\alpha} _{n}^{i}&\mathbf {d} _{n}\\0&0&1\\0&0&0\end{bmatrix }}\w \mathbb {R} ^{(d+2)\razy (d+2)},}$

${\ Displaystyle \ mathbf {L} = \ lewo [{\ rozpocząć {tablica} {ll} \ mathbf {I} & \ mathbf {0} _ {d \ razy 2} \ koniec { tablica}} \ prawej]}$ i ${\ Displaystyle \ mathbf {r} ^ {\ intercal} = \ lewo [{\ rozpocząć {tablica} ll}\mathbf {0} _{1\times (d+1)}&1\end{array}}\right],h_{n}\leq \tau }$ i ${\ displaystyle p + q> 1}$ . Tutaj macierze $\ Displaystyle \ mathbf {A} _ {n}}$ , ${\ Displaystyle \ mathbf {B} _ {n} ^ {i}}$ , ${\ Displaystyle \ mathbf {c } _ {n}}$ i ${\ Displaystyle \ mathbf {d} _ {n}}$ są zdefiniowane jak w (5.2), ale zastępując ${z}$$y} }$${\ Displaystyle \ mathbf$ i ${\ Displaystyle \ mathbf {\ alfa} _ {n} ^ {i} = (\ mathbf {y} (t_ { n+1}-\tau _{i})-\mathbf {y} (t_{n}-\tau _{i}))/h_{n},}$ gdzie

${\ Displaystyle \ mathbf {y} \ lewo (t \ prawo)=\mathbf {y} _{n_{t}}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{ n_{t}}(t-t_{n_{t}})))^{2^{k_{n}}}\mathbf {r} ,}$

gdzie ${\ Displaystyle n_ {t} = \ max \ {n = 0,1,2, ...,: t_ {n} \ równoważnik t {\ tekst { i }}t_{n}\in \left(t\right)_{h}\}}$ , jest Lokalnym Przybliżeniem Liniowym rozwiązania (5.1) określonym schematem LL (5.3) dla wszystkich ${\ Displaystyle t \ w \ lbrack t_ {0}, t_ {n}]}$ i przez ${\ Displaystyle \ mathbf {y} \ lewo (t \ prawej) = \ mathbf {\ varphi} \ lewo (t \ prawej)}$ dla ${\ Displaystyle t \ w \ lewo [t_ {0} - \ tau, t_ {0} \ prawo]}$ . Dla dużych systemów DDE

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n} + \ mathbf {L \ mathbf {k}} _ {m_ {n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )\quad i\quad \mathbf {y} \left( t\right)=\mathbf {y} _{n_{t}}+\mathbf {L\mathbf {k}} _{m_{n_{t}},k_{n_{t}}}^{p, q}(t-t_{n_{t}},\mathbf {M} _{n_{t}},\mathbf {r} ),}$

z ${\ displaystyle p + q> 1}$ i ${\ displaystyle m_ {n}> 2}$ . Rys. 2 ilustruje stabilność schematu LL (5.3) oraz jawnego schematu podobnego rzędu w integracji sztywnego systemu DDE.

Metody LL dla RDE

Rozważ d- wymiarowe losowe równanie różniczkowe (RDE)

${\ Displaystyle {\ Frac {d \ mathbf {x} \ lewo (t \ w prawo)}{dt}}=\mathbf {f} (\mathbf {x} (t),\mathbf {\xi } (t)),\quad t\in \left[t_{0},T\right ],\qquad \qquad \qquad (6.1)}$

z warunkiem początkowym ${\ Displaystyle \ mathbf {x} (t_ {0}) = \ mathbf {x} _ {0},}$ gdzie jest ${\ Displaystyle \ mathbf {\ xi}}$ k -wymiarowy rozdzielny skończony ciągły proces stochastyczny , a f jest funkcją różniczkowalną. Załóżmy, że podana jest realizacja (ścieżka) ${\ displaystyle \ mathbf {\ xi}} .$

Lokalna dyskretyzacja liniowa

Dla dyskretyzacji czasu ${\ Displaystyle \ lewo (t \ prawej) _ {h}}$ , lokalna liniowa dyskretyzacja RDE (6.1) w każdym punkcie ${\ displaystyle t_ {n+1}\in \left(t\right)_{h}}$ jest zdefiniowane przez wyrażenie rekurencyjne

${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \mathbf {\phi} (t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{z }}\qquad \mathbf {z} _{0}=\ matematykaf {x} _{0},}$

Gdzie

${\ Displaystyle \ mathbf {\ fi} (t_ {n}, \ mathbf {z} _ {n}; h_ {n}) = \ int \ ograniczenia _ {0} ^ {h_ {n}} e ^ {\ mathbf {f} _{\mathbf {x}}(\mathbf {z} _{n},\mathbf {\xi} (t_{n}))(h_{n}-u)}(\mathbf {f (z} _{n},\mathbf {\xi} (t_{n}))+\mathbf {f} _{\mathbf {\xi}}(\mathbf {z} _{n},\mathbf { \xi} (t_{n}))({\widetilde {\mathbf {\xi}}}(t_{n}+u)-{\widetilde {\mathbf {\xi}}}(t_{n}) ))\,du}$

i $jest$${\ Displaystyle t \ w \ lewo [t_ {0}, T \ prawo].}$ procesu dla $_$ Tutaj ${\ Displaystyle \ mathbf {f} _ {x}}$ i ${\ Displaystyle \ mathbf {f} _ { \ xi }}$ oznaczają pochodne cząstkowe względem ${\ displaystyle \ mathbf {f}}$$\ mathbf {x}}$$odpowiednio$ i .

Lokalne schematy linearyzacji

Rys. 3 Portret fazowy trajektorii schematów Eulera i LL w całkowaniu nieliniowego RDE (6.2)–(6.3) o wielkości kroku h = 1/32 i p = q = 6.

$phi } }$ zależności od przybliżeń do procesu i algorytmu do obliczania $}}}}$${\ xi$$mathbf$ , można zdefiniować różne schematy linearyzacji lokalnych. Każda numeryczna implementacja $nazywana$ dyskretyzacji liniowej $jest$ ogólnie schematem

schematy LL

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2 ^{k_{n}}}\mathbf {r,} \quad }$

gdzie macierze są zdefiniowane jako ${\ Displaystyle \ mathbf {M} _ {n}, \ quad \ mathbf {L} \ quad i \ quad \ mathbf {r}}$

${\ Displaystyle \ mathbf {M} _ {n} = \ lewo [{\ rozpocząć {tablica} {ccc} \ mathbf {f} _ {\ mathbf {x}} \ lewo (\ mathbf {y } _{n},\mathbf {\xi} (t_{n})\right)&\mathbf {f} _{\mathbf {\xi}}(\mathbf {y} _{n},\mathbf { \xi} (t_{n})(\mathbf {\xi} (t_{n+1})-\mathbf {\xi} (t_{n}))/h_{n}&\mathbf {f} \ left(\mathbf {y} _{n},\mathbf {\xi} (t_{n})\right)\\0&0&1\\0&0&0\end{tablica}}\right]}$

${\ Displaystyle \ mathbf {L} = \ lewo [{\ rozpocząć {tablica} {ll} \ mathbf {I} & \ mathbf {0} _ {d \ razy 2} \ koniec { tablica}}\right]}$ , ${\ Displaystyle \ mathbf {r} ^ {\ intercal} = \ lewo [{\ rozpocząć {tablica} {ll} \ mathbf { 0} _{1\times (d+1)}&1\end{array}}\right]}$ i p+q>1 . W przypadku dużych systemów RDE,

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n} + \ mathbf {L \ mathbf {k}} _ {m_ {n}, k_ {n}} ^ {p ,q}(h_{n},\mathbf {M} _{n},\mathbf {r} ),\quad p+q>1\quad i\quad m_{n}>2.}$

Współczynnik zbieżności obu schematów wynosi ${\ Displaystyle min \ {2,2 \ gamma \}}$ , gdzie jest wykładnikiem warunku posiadacza $\ gamma$$} styl wyświetlania \mathbf {\xi}}$ .

Rysunek 3 przedstawia portret fazowy RDE

${\ Displaystyle {\ Frac {dx_ {1}} {dt}} = - x_ {2} + \ lewo (1-x_ {1} ^ {2} -x_ {2} ^ {2} \ prawej) x_ { 1}\sin(w^{H}(t))^{2},\quad \qquad x_{1}(0)=0,8\qquad (6,2)}$

${\ Displaystyle {\ Frac {dx_ {2}} {dt}} = x_ {1} + (1-x_ {1} ^ {2} -x_ {2} ^ {2}) x_ {2} \ sin ( w^{H}(t))^{2},\qquad \qquad x_{2}(0)=0,1,\qquad (6,3)}$

i jego przybliżenie za pomocą dwóch schematów numerycznych, gdzie oznacza $Browna$ proces z wykładnikiem Hursta H = 0,45

Silne metody LL dla SDE

Rozważ d -wymiarowe stochastyczne równanie różniczkowe (SDE)

${\ Displaystyle d \ mathbf {x} (t) = \ mathbf {f} (t, \ mathbf {x} (t)) dt + \ suma \ limity _ {i = 1} ^ {m} \ mathbf {g} _{i}(t)d\mathbf {w} ^{i}(t),\quad t\in \left[t_{0},T\right],\qquad \qquad \qquad (7.1)}$

z warunkiem początkowym ${0}}$ _ , gdzie współczynnik dryfu i ${\ Displaystyle \ mathbf {f}}$ sol ${\ Displaystyle \ mathbf {g} _ {i}}$ są funkcjami różniczkowalnymi i ${\ Displaystyle \ mathbf {w = (\ mathbf {w}}$ jest m -wymiarowy standardowy proces Wienera .

Lokalna dyskretyzacja liniowa

Dla dyskretyzacji czasu ${\ Displaystyle \ lewo (t \ prawej) _ {h}}$ , kolejność - ${\ Displaystyle \ mathbb {\ gamma}}$ (= 1,1,5) Silna lokalna liniowa dyskretyzacja rozwiązanie SDE (7.1) jest określone relacją rekurencyjną

${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} _ {\ mathbb {\ gamma}} (t_ {n}, \ mathbf {z } _{n};h_{n})+\mathbf {\xi} (t_{n},\mathbf {z} _{n};h_{n}),\quad z\quad \mathbf {z} _{0}=\mathbf {x} _{0},}$

Gdzie

${\ Displaystyle \ mathbf {\ phi} _ {\ mathbb {\ gamma}} (t_ {n}, \ mathbf {z} _ {n}; \ delta) = \ int _ {0} ^ {\ delta} e ^{\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {y} _{n})(\delta -u)}(\mathbf {f(} t_{n}, \mathbf {z} _{n})+\mathbf {a} ^{\mathbb {\gamma}}(t_{n},\mathbf {z} _{n})u)du}$

I

${\ Displaystyle \ mathbf {\ xi} \ lewo (t_ {n}, \ mathbf {z} _ {n}; \ delta \ po prawej) = \ suma \ limity _ {i = 1} ^ {m} \ int \ nolimits _{t_{n}}^{t_{n}+\delta}e^{\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n}) (t_{n}+\delta -u)}\mathbf {g} _{i}(u)\,d\mathbf {w} ^{i}(u).}$

Tutaj,

${\ Displaystyle \ mathbf {a} ^ {\ mathbb {\ gamma}} (t_ {n}, \ mathbf {z} _ {n}) = \ lewo \ {{\ rozpocząć {tablica} {cl} \ mathbf { f} _{t}(t_{n},\mathbf {z} _{n})&{\text{for}}\qquad \mathbb {\gamma} =1\\\mathbf {f} _{t }(t_{n},\mathbf {z} _{n})+{\frac {1}{2}}\sum \limits _{j=1}^{m}(\mathbf {I} \otimes \mathbf {g} _{j}^{\intercal}(t_{n})}\mathbf {f} _{\mathbf {xx}}(t_{n},\mathbf {z} _{n}) \mathbf {g} _{j}(t_{n})&{\text{for}}\quad \mathbb {\gamma} =1,5,\end{tablica}}\right.}$

${\ Displaystyle \ mathbf {f} _ {\ mathbf {x}} \ mathbf {f} _ {t}}$ oznaczają pochodne cząstkowe względem ${\ Displaystyle \ mathbf {f}}$$} }$ zmienne ${ \$ t , oraz macierz Hesji z $xx}}}$$mathbf {$ w odniesieniu do ${\ Displaystyle \ mathbf {x}}$ . Silna lokalna dyskretyzacja liniowa $z} _ {n + 1}}$ się z porządkiem $\ displaystyle \ mathbf {$ = 1, 1,5) do rozwiązania (7,1) z ).

Lokalne dyskretyzacje liniowe wysokiego rzędu

Po lokalnej linearyzacji składnika dryfu (7.1) w ${\ Displaystyle (t_ {n}, \ mathbf {z} _ {n})}$ równanie reszty ${\ displaystyle \mathbf {r} }$ jest podane przez

${\ Displaystyle d \ mathbf {r} (t) = \ mathbf {q} _ {\ gamma} (t_ {n}, \ mathbf {z} _ {n}; t \ mathbf {\ mathbf {r}} (t))\,dt+\sum \limits _{i=1}^{m}\mathbf {g} _{i}(t)\,d\mathbf {w} ^{i}(t)\mathbf {,} \qquad \mathbf {r} (t_{n})=\mathbf {0} }$

dla wszystkich ${\ Displaystyle t \ w \ lbrack t_ {n}, t_ {n + 1}]} ,$ gdzie

${\ Displaystyle \ mathbf {q} _ {\ gamma} (t_ {n}, \ mathbf {z} _ {n}; s \ mathbf {, \ xi}) = \ mathbf {f} (s, \ mathbf { z} _{n}+\mathbf {\phi} _{\gamma}(t_{n},\mathbf {z} _{n};s-t_{n})+\mathbf {\xi} )- \mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n})\mathbf {\phi} _{\gamma}(t_{n},\mathbf {z } _{n};s-t_{n})-\mathbf {a} ^{\gamma }(t_{n},\mathbf {z} _{n})(s-t_{n})-\ mathbf {f} (t_{n},\mathbf {z} _{n}).}$

Lokalna $7.1$ liniowa wysokiego SDE ) w definiowana wyrażenie

${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} _ {\ gamma} (t_ {n}, \ mathbf {z} _ {n };h_{n})+{\widetilde {\mathbf {r}}}(t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{z}} \qquad \mathbf {z} _{0}=\mathbf {x} _{0},}$

gdzie $jest$ silnym przybliżeniem reszty rzędu $wyższej$$\ displaystyle \$ niż 1,5 . Silna dyskretyzacja HOLL $z$$.$ do (7.1

Lokalne schematy linearyzacji

W zależności od sposobu obliczania ${\ Displaystyle \ mathbf {\ phi} _ {\ mathbb {\ gamma}}}$ , ${\ Displaystyle \ mathbf {\ xi}}$ i ${\ Displaystyle {\ widetilde {\ mathbf {r} }}}$ można uzyskać różne schematy numeryczne. Każda numeryczna implementacja $}$ lokalnej dyskretyzacji liniowej dowolnego rzędu jest ogólnie nazywana silną lokalną linearyzacją (SLL) y $\ displaystyle \ mathbf {y} _ {n$ ) schemat .

Zamów 1 schemat SLL

${\ Displaystyle \ mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r+} \sum \limits _{i=1}^{m}\mathbf {g} _{ i}(t_{n})\Delta \mathbf {w} _{n}^{i},\quad }$ ${\ Displaystyle \ qquad \ qquad (7.2)}$

gdzie macierze są zdefiniowane ${\ Displaystyle \ Delta \ mathbf {w} _ {n} ^ {i}}$ w (4.6), Δ $\ mathbf {M} _ {n}}$$\ Displaystyle$ i ${\ Displaystyle \ mathbf {R}}$ jest iid zerową średnią zmienną losową Gaussa $i$ wariancją p + q > 1. duże systemy SDE, w powyższym schemacie ${\ Displaystyle (\ mathbf {P} _ {p, q} (2 ^ {- k_ {n}} \ mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} } jest$ zastępowane przez ${\ Displaystyle \ mathbf {\ mathbf {k}} _ {m_ {n}, k_ {n}} ^ {p, q} (h_ {n}, \ mathbf {M} _ {n}, \ mathbf {r } )}$ .

Zamów 1,5 schematu SLL

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n} + \ mathbf {L} (\ mathbf {P} _ {p, q} (2 ^ {-k_ {n }}\mathbf {M} _{n}h_{n}})^{2^{k_{n}}}\mathbf {r} +\sum \limits _{i=1}^{m}\left (\mathbf {g} _{i}(t_{n})\Delta \mathbf {w} _{n}^{i}\mathbf {f} _{\mathbf {x}}(t_{n}, {\widetilde {\mathbf {y}}}_{n})\mathbf {g} _{i}(t_{n})\Delta \mathbf {z} _{n}^{i}+{\frac {d\mathbf {g} _{i}(t_{n})}{dt}}(\Delta \mathbf {w} _{n}^{i}h_{n}-\Delta \mathbf {z} _{n}^{i})\right),\qquad \qquad (7.3)}$

gdzie macierze są zdefiniowane jako ${\ Displaystyle \ mathbf {M} _ {n}}$ , ${\ Displaystyle \ mathbf {L}}}$ i ${\ Displaystyle \ mathbf {r}}$

${\ Displaystyle \ mathbf {M} _ {n} = {\ rozpocząć {bmatrix} \ mathbf {f} _ {\ mathbf {x}} (t_ {n}, \ mathbf {y} _ {n}) i \ mathbf {f} _{t}(t_{n},\mathbf {y} _{n})+{\frac {1}{2}}\sum \limits _{j=1}^{m}\ left(\mathbf {I} \otimes \mathbf {g} _{j}^{\intercal}(t_{n})\right)\mathbf {f} _{\mathbf {xx}}(t_{n} ,\mathbf {y} _{n})\mathbf {g} _{j}(t_{n})&\mathbf {f} (t_{n},\mathbf {y} _{n})\\ 0&0&1\\0&0&0\end{bmatrix}}\w \mathbb {R} ^{(d+2)\times (d+2)},}$

${\ Displaystyle \ mathbf {L} = \ lewo [{\ rozpocząć {tablica} {ll} \ mathbf {I} & \ mathbf {0} _{d\times 2}\end{tablica}}\right],\mathbf {r} ^{\intercal }=\left[{\begin{array}{ll}\mathbf {0} _ {1 \ razy (d + 1)} i 1 \ koniec {tablica}} \ prawej]}$ , ${\ Displaystyle \ Delta \ mathbf {z} _ {n} ^ {i}}$ mi $\ mathbf {z} _ {n} ^ {i}) ^{2}\right)={\frac {1}{3}}h_{n}^{3}}$ i kowariancji ${\ Displaystyle E (\ Delta \ mathbf {w} _ {n} ^ {i} \ Delta \ mathbf {z} _ {n} ^ {i}) = {\ Frac {1} {2}} h_ {n }^{2}}$ i p+q>1 . W przypadku dużych systemów SDE, w powyższym schemacie ${\ Displaystyle (\ mathbf {P} _ {p, q} (2 ^ {- k_{n}}\mathbf {M} _{n}h_{n}})^{2^{k_{n}}}\mathbf {r} } jest zastępowane$ przez ${\ Displaystyle \ mathbf {\ mathbf {k}} _ {m_ {n}, k_ {n}} ^ {p, q} (h_ {n}, \ mathbf { M} _ {n},\mathbf {r} )}$ .

Zamów 2 schematy SLL-Taylor

${\ Displaystyle \ mathbf {y} _ {t_ {n + 1}} = \ mathbf {y} _ {n} + \ mathbf {L} (\ mathbf {P} _ {p, q} (2 ^ {- k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} +\sum \limits _{j=1}^{m }\mathbf {g} _{j}\left(t_{n}\right)\Delta \mathbf {w} _{n}^{j}+\sum \limits _{j=1}^{m} \mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {y} _{n})\mathbf {g} _{j}\left(t_{n}\right){\ widetilde {J}}_{\left(j,0\right)}+\sum \limits _{j=1}^{m}{\frac {d\mathbf {g} _{_{j}}} {dt}}\left(t_{n}\right){\widetilde {J}}_{\left(0,j\right)}}$

${\ Displaystyle \ qquad \ qquad + \ suma \ ograniczenia _ {j_ {1}, j_ {2} = 1} ^ {m} \ lewo (\ mathbf {I} \ czasami \ mathbf {g} _ {j_ {2} }}^{\intercal }\left(t_{n}\right)\right)\mathbf {f} _{\mathbf {xx}}(t_{n},\mathbf {y} _{n})\ mathbf {g} _{j_{1}}\left(t_{n}\right){\widetilde {J}}_{\left(j_{1},j_{2},0\right),}\ qquad \qquad (7.4)}$

gdzie ${\ Displaystyle \ mathbf {M} _ {n}}$ , ${\ Displaystyle \ mathbf {L}}$ , ${\ Displaystyle \ mathbf {r}}$ i ${\ Displaystyle \ Delta \ mathbf {w} _ {n} ^ {i}}$ są zdefiniowane jak w schematach SLL rzędu 1, a jest przybliżeniem rzędu 2 do wielokrotności ${\ Displaystyle {\ widetilde {J}} _ {\ alfa}}$ Całka Stratonovisha jot $\ Displaystyle J _ {\ alfa}}$ .

Zamów 2 schematy SLL-RK

Ryc. 4, góra : Ewolucja domen w płaszczyźnie fazowej oscylatora harmonicznego (7.6), przy ε=0 i ω=σ=1. Obrazy początkowego okręgu jednostkowego (kolor zielony) uzyskuje się w trzech momentach czasu T za pomocą rozwiązania dokładnego (kolor czarny) oraz schematów SLL1 (kolor niebieski) i Implicit Euler (kolor czerwony) z h=0,05 . Dół : Oczekiwana wartość energii (linia ciągła) wzdłuż rozwiązania nieliniowego oscylatora (7.6), przy ε=1 i ω=100, oraz jej przybliżenie (okręgi) obliczone metodą Monte Carlo z 10000 symulacji SLL1 z h=1/2 i p=q=6 .

Dla SDE z pojedynczym szumem Wienera (m=1 )

${\ Displaystyle \ mathbf {y} _ {t_ {n + 1}} = \ mathbf {y} _ {n} + {\ widetilde {\ mathbf {\ phi } }}(t_{n},\mathbf {y} _{n};h_{n})+{\frac {h_{n}}{2}}\left(\mathbf {k} _{1 }+\mathbf {k} _{2}\right)+\mathbf {g} \left(t_{n}\right)\Delta w_{n}+{\frac {\left(\mathbf {g} \ left(t_{n+1}\right)-\mathbf {g} \left(t_{n}\right)\right)}{h_{n}}}J_{\left(0,1\right)} \quad (7.5)}$

${\ Displaystyle \ quad \ quad \ quad}$

Gdzie

${\ Displaystyle \ mathbf {k} _ {1} = \ mathbf {f} (t_ {n} + {\ Frac {h_ {n}}} {2}}, \ mathbf {y} _ {n} + {\ widetilde {\mathbf {\phi}}}(t_{n},\mathbf {y} _{n};{\frac {h_{n}}{2}})+\gamma _{+})-\ mathbf {f} _ {\mathbf {x}}(t_{n},\mathbf {y} _{n}){\widetilde {\mathbf {\phi}}}(t_{n},\mathbf {y } _{n};{\frac {h_{n}}{2}})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf { f} _{t}\left(t_{n},\mathbf {y} _{n}\right){\frac {h_{n}}{2}},}$

${\ Displaystyle \ mathbf {k} _ {2} = \ mathbf {f} (t_ {n} + {\ Frac {h_ {n}}} {2}}, \ mathbf {y} _ { n}+{\widetilde {\mathbf {\phi}}}(t_{n},\mathbf {y} _{n};{\frac {h_{n}}{2}})+\gamma _{ -})-\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {y} _{n}){\widetilde {\mathbf {\phi}}}(t_{n} ,\mathbf {y} _{n};{\frac {h_{n}}{2}})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right )-\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right){\frac {h_{n}}{2}},}$

z ${\ Displaystyle \ gamma _ {\ pm} = {\ Frac {1} {h_ {n}}} \ mathbf {g} \ lewo (t_ {n} \ prawo) {\ Bigl (} {\ widetilde {J} } _ {\ lewo (1,0 \ prawo)} \ pm {\ sqrt {2 {\ widetilde {J}} _ {\ lewo (1,1,0 \ prawo)} h_ {n} - {\ widetilde { J}}_{\left(1,0\right)}^{2}}}{\Bigr )}}$ .

$widetilde {\ mathbf {\ fi}} }(t_{n},\mathbf {y} _{n};h_{n})=\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}} \mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} }$ ) dla niskowymiarowych SDE i ${\ Displaystyle {\ widetilde {\ mathbf {\ fi}}} (t_ {n },\mathbf {y} _{n};h_{n})=\mathbf {L\mathbf {k}} _{m_{n},k_{n}}^{p,q}(h_{n }, \ mathbf {M} _ {n}, \ mathbf {r} )}$ dla dużych systemów SDE, gdzie ${\ Displaystyle \ mathbf {M} _ {n}}$ L ${\ Displaystyle \ mathbf {L}}$ , ${\ Displaystyle \ mathbf {r}}$ Δ $\ Displaystyle \ Delta \ mathbf {w} _ {n} ^ {i}}$ i ${\ Displaystyle {\ widetilde {J}} _ {\ alfa}}$ są zdefiniowane w kolejności - 2 schematy SLL-Taylor, p + q> 1 i ${\ Displaystyle m_ {n}> 2}$ .

Stabilność i dynamika

Z konstrukcji, silne dyskretyzacje LL i HOLL dziedziczą stabilność i dynamikę liniowych SDE, ale ogólnie nie jest tak w przypadku silnych schematów LL. $sztywne i wysoce oscylacyjne$ 7.2 ) - (7.5) z A . Co więcej, w przypadku liniowych SDE z losowymi atraktorami schematy te mają również losowy atraktor, który jest zbieżny pod względem prawdopodobieństwa do dokładnego, gdy wielkość kroku maleje i zachowuje ergodyczność tych równań dla dowolnej wielkości kroku. Schematy te odtwarzają również podstawowe właściwości dynamiczne prostych i sprzężonych oscylatorów harmonicznych, takie jak liniowy wzrost energii wzdłuż ścieżek, zachowanie oscylacyjne wokół 0, symplektyczna struktura oscylatorów hamiltonowskich i średnia ścieżek. Dla nieliniowych SDE z małym szumem (tj. (7.1) z ${\ Displaystyle \ mathbf {g} _ {i} (t) \ około 0}$ ), ścieżki tych schematów SLL są w zasadzie nielosowymi ścieżkami schematu LL (4.6) dla ODE plus małe zakłócenie związane z małym szumem. W tej sytuacji właściwości dynamiczne tego schematu deterministycznego, takie jak zachowanie linearyzacji i zachowanie dokładnej dynamiki rozwiązania wokół punktów równowagi hiperbolicznej i orbit okresowych, stają się istotne dla ścieżek schematu SLL. Na przykład ryc. 4 przedstawia ewolucję domen w płaszczyźnie fazowej i energii oscylatora stochastycznego

${\ Displaystyle {\ rozpocząć {tablica} {ll} dx (t) = y (t) dt, & x_ {1} (0) = 0,01 \\ dy (t) = - (\ omega ^ {2}x(t)+\epsilon x^{4}(t))dt+\sigma dw_{t},&x_{1}(0)=0.1,\end{tablica}}\qquad \qquad (7.6) }$

oraz ich przybliżenia za pomocą dwóch schematów numerycznych.

Słabe metody LL dla SDE

Rozważ d -wymiarowe stochastyczne równanie różniczkowe

${\ Displaystyle d \ mathbf {x} (t) = \ mathbf {f} (t, \ mathbf {x} (t)) dt + \ suma \ limity _ {i = 1} ^ {m} \ mathbf {g} _{i}(t)d\mathbf {w} ^{i}(t),\qquad t\in \left[t_{0},T\right],\qquad \qquad (8.1)}$

z warunkiem początkowym ${\ Displaystyle \ mathbf {x} (t_ {0}) = \ mathbf {x} _ {0}}$ , gdzie współczynnik dryfu i ${\ Displaystyle \ mathbf {f}}$ sol ${\ Displaystyle \ mathbf {g} _ {i}}$ są funkcjami różniczkowalnymi i ${\ Displaystyle \ mathbf {w = (\ mathbf {w}}$ jest m -wymiarowy standardowy proces Wienera.

Lokalna dyskretyzacja liniowa

Dla dyskretyzacji czasu ${\ Displaystyle \ lewo (t \ prawej) _ {h}}$ , kolejność - ${\ Displaystyle \ mathbb {\ beta} }$${\ Displaystyle (= 1 ,2)}$ Słaba lokalna dyskretyzacja liniowa rozwiązania SDE (8.1) jest zdefiniowana przez relację rekurencyjną

${\ Displaystyle \ mathbf {z} _ {n + 1} = \ mathbf {z} _ {n} + \ mathbf {\ fi} _ {\ mathbb {\ beta}} (t_ {n}, \ mathbf {z } _{n};h_{n})+\mathbf {\eta} (t_{n},\mathbf {z} _{n};h_{n}),\quad z\quad \mathbf {z} _{0}=\mathbf {x} _{0},}$

Gdzie

${\ Displaystyle \ mathbf {\ phi} _ {\ mathbb {\ beta}} (t_ {n}, \ mathbf {z} _ {n}; \ delta) = \ int _ {0} ^ {\ delta} e ^{\mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n})(\delta -u)}(\mathbf {f(} t_{n}, \mathbf {z} _{n})+\mathbf {b} ^{\mathbb {\beta}}(t_{n},\mathbf {z} _{n})u)du}$

z

${\ Displaystyle \ mathbf {b} ^ {\ mathbb {\ beta}} (t_ {n}, \ mathbf {z} _ {n}) = {\ rozpocząć {przypadki} \ mathbf {f} _ {t} ( t_{n},\mathbf {z} _{n})&{\text{for }}\mathbb {\beta } =1\\\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})+{\frac {1}{2}}\sum \limits _{j=1}^{m}\left(\mathbf {I} \otimes \mathbf {g} _{ j}^{\intercal }\left(t_{n}\right)\right)\mathbf {f} _{\mathbf {xx}}(t_{n},\mathbf {z} _{n})\ mathbf {g} _{j}\left(t_{n}\right)&{\text{for}}\mathbb {\beta} =2,\end{przypadki}}}$

i $_$ _

${\ Displaystyle \ mathbf {\ Sigma} (t_ {n}, \ mathbf {z} _ {n}; \ delta) = \ int \ granice _ {0} ^ {\ delta} e ^ {\ mathbf {f} _{\mathbf {x}}(t_{n},\mathbf {z} _{n})(\delta -s)}\mathbf {G} (t_{n}+s)\mathbf {G} ^ {\intercal}(t_{n}+s)e^{\mathbf {f} _{\mathbf {x}}^{\intercal}(t_{n},\mathbf {z} _{n})( \delta -s)}ds.}$

Tutaj oznaczamy pochodne cząstkowe ${\ Displaystyle \ mathbf {f} _ {\ mathbf {x}}}$ , $} _ {t}}$$Displaystyle \ mathbf {$ w odniesieniu do zmiennych odpowiednio ${\ Displaystyle \ mathbf {x}}$ i t , odpowiednio ${\ Displaystyle \ mathbf {f} _ {\ mathbf {xx}}}$ heskiej macierzy ${\ displaystyle \mathbf {f} }$ względem ${\ Displaystyle \ mathbf {x}}$ i ${\ Displaystyle \ mathbf {G} (t) = [\ mathbf {g} _ {1}(t),\ldots,\mathbf {g} _{m}(t)]}$ . Słaba lokalna dyskretyzacja liniowa $Displaystyle \ mathbf {$ się z kolejnością $z} _ {n + 1} }$ (=1,2) do rozwiązania (8.1).

Lokalne schematy linearyzacji

W $zależności$ od sposobu obliczania $i$ uzyskać różne schematy $jest$ implementacja $($ lokalnej dyskretyzacji liniowej ogólnie nazywana schematem słabej lokalnej linearyzacji .

Zamów 1 schemat WLL

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n} + \ mathbf {B} _{14}+(\mathbf {B} _{12}\mathbf {B} _{11}^{\intercal})^{1/2}\mathbf {\xi} _{n}}$

gdzie dla SDE z autonomicznymi współczynnikami dyfuzji i ${\ Displaystyle \ mathbf {B} _ {11}}$ , ${\ Displaystyle \ mathbf {B} _ {12}}$ i ${\ Displaystyle \ mathbf {B } _{14}}$ to podmacierze określone przez podzieloną macierz ${\ Displaystyle \ mathbf {B} = \ mathbf {P} _ {p, q} (2 ^ {- k_ {n}} {\ mathcal {M}} _ {n} h_ {n}}) ^ {2 ^{k_{n}}}}$ , z

${\ Displaystyle {\ mathcal {M}} _ {n} = \ lewo [{\ rozpocząć {tablica} {cccc} \ mathbf {f} _ {\ mathbf {x}} ( t_{n},\mathbf {y} _{n})&\mathbf {GG} ^{\intercal}&\mathbf {f} _{t}(t_{n},\mathbf {y} _{n })&\mathbf {f} (t_{n},\mathbf {y} _{n})\\\mathbf {0} &-\mathbf {f} _{\mathbf {x} }^{\intercal }(t_{n},\mathbf {y} _{n})&\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &0&1\\\mathbf {0} &\mathbf {0} &0&0\end{array}}\right]\in \mathbb {R} ^{(2d+2)\times (2d+2)},}$

i ${\ Displaystyle \ {\ mathbf {\ xi} _ {n} \}}$ jest sekwencją d - wymiarowych niezależnych dwupunktowych wektorów losowych o rozkładzie spełniających ${\ Displaystyle P (\ xi _ {n} ^ {k} = \ pm 1) = {\ Frac {1} {2}}}$ .

Zamów schemat 2 WLL

${\ Displaystyle \ mathbf {y} _ {n + 1} = \ mathbf {y} _ {n} + \ mathbf {B} _{16}+(\mathbf {B} _{14}\mathbf {B} _{11}^{\intercal})^{1/2}\mathbf {\xi} _{n} ,}$

gdzie ${\ Displaystyle \ mathbf {B} _ {11}}$ , ${\ Displaystyle \ mathbf {B} _ {14}}$ i ${\ Displaystyle \ mathbf {B} _ {16}}$ są $2 ^ { -k_{n}}{\mathcal {M}}_{n}h_{n}})^{2^{k_{n}}}}$ k z

${\ Displaystyle {\ mathcal { M}}_{n}=\left[{\begin{array}{cccccc}\mathbf {J} &\mathbf {H} _{2}&\mathbf {H} _{1}&\mathbf {H } _{0}&\mathbf {a} _{2}&\mathbf {a} _{1}\\\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {I} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {I} & \mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {0} &\ mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} &0&1\\\mathbf {0} &\mathbf {0} &\mathbf {0} & \mathbf {0} &0&0\end{array}}\right]\in \mathbb {R} ^{(4d+2)\times (4d+2)},}$

${\ Displaystyle \ mathbf {J} = \ mathbf {f} _ {\ mathbf {x}} (t_ {n} \ mathbf {y } _{n})\qquad \mathbf {a} _{1}=\mathbf {f} (t_{n},\mathbf {y} _{n})\qquad \mathbf {a} _{2} =\mathbf {f} _{t}(t_{n},\mathbf {y} _{n})+{\frac {1}{2}}\sum \limits _{i=1}^{m }(\mathbf {I} \otimes (\mathbf {g} ^{i}(t_{n}))^{\intercal})\mathbf {f} _{\mathbf {xx} }(t_{n} ,\mathbf {y} _{n})\mathbf {g} ^{i}(t_{n})}$

I

${\ Displaystyle \ mathbf {H} _ {0} = \ mathbf {G} (t_ {n}) \ mathbf {G} ^ {\ intercal} (t_ {n}) \ qquad \ mathbf {H} _ {1 }=\mathbf {G} (t_{n}){\frac {d\mathbf {G} ^{\intercal}(t_{n})}{dt}}+{\frac {d\mathbf {G} (t_{n})}{dt}}\mathbf {G} ^{\intercal}(t_{n})\qquad \mathbf {H} _{2}={\frac {d\mathbf {G} ( t_{n})}{dt}}{\frac {d\mathbf {G} ^{\intercal}(t_{n})}{dt}}{\text{.}}}$

Stabilność i dynamika

Ryc. 5 Przybliżona średnia SDE (8.2) obliczona metodą Monte Carlo ze 100 symulacjami różnych schematów z h=1/16 i p=q=6 .

Z założenia słabe dyskretyzacje LL dziedziczą stabilność i dynamikę liniowych SDE, ale ogólnie nie jest tak w przypadku słabych schematów LL. Schematy WLL z $zachowaniem dwóch$ pierwszych momentów średniokwadratowej, jaką może . Obejmuje to na przykład równania sprzężonych oscylatorów harmonicznych napędzanych siłą losową oraz duże układy sztywnych liniowych SDE, które wynikają z metody linii dla liniowych stochastycznych równań różniczkowych cząstkowych. Ponadto te schematy WLL zachowują ergodyczność równań liniowych i są geometrycznie ergodyczne dla niektórych klas nieliniowych SDE. Dla nieliniowych SDE z małym szumem (tj. (8.1) z ${\ Displaystyle \ mathbf {g} _ {i} (t) \ około 0}$ ), rozwiązaniami tych schematów WLL są w zasadzie nielosowe ścieżki schematu LL (4.6) dla ODE plus małe zakłócenie związane z małym szumem. W tej sytuacji właściwości dynamiczne tego schematu deterministycznego, takie jak zachowanie linearyzacji i zachowanie dokładnej dynamiki rozwiązania wokół punktów równowagi hiperbolicznej i orbit okresowych, stają się istotne dla średniej schematu WLL. Na przykład ryc. 5 przedstawia przybliżoną średnią SDE

${\ Displaystyle dx = - t ^ {2} x {\ text{ }}dt+{\frac {3}{2(t+1)}}e^{-t^{3}/3}{\text{ }}dw_{t},\qquad \qquad x(0 )=1,\qquad \quad (8.2)}$

obliczane różnymi schematami.

Notatki historyczne

Poniżej znajduje się oś czasu przedstawiająca główne zmiany metody linearyzacji lokalnej (LL).

• Pope DA (1963) wprowadza dyskretyzację LL dla ODE i schemat LL oparty na rozwinięciu Taylora.
• Ozaki T. (1985) wprowadza metodę LL do całkowania i szacowania SDE. Po raz pierwszy użyto terminu „linearyzacja lokalna”.
• Biskajski R. i in. (1996) przeformułowali metodę silnego LL dla SDE.
• Shoji I. i Ozaki T. (1997) przeformułowali metodę słabego LL dla SDE.
• Hochbrück M. i in. (1998) wprowadzają schemat LL dla ODE oparty na aproksymacji podprzestrzeni Kryłowa.
• Jimenez JC (2002) wprowadza schemat LL dla ODE i SDE oparty na racjonalnym przybliżeniu Padé.
• Carbonell FM i in. (2005) wprowadzają metodę LL dla RDE.
• Jimenez JC i in. (2006) przedstawiają metodę LL dla DDE.
• De la Cruz H. i in. (2006,2007) i Tokman M. (2006) przedstawiają dwie klasy integratorów HOLL dla ODE: oparte na integratorze i oparte na kwadraturze.
• De la Cruz H. i in. (2010) wprowadzili silną metodę HOLL dla SDE.