Multilateracja rzeczywistego zakresu

Multilateracja rzeczywistego zasięgu (nazywana również multilateracją zakresu i multilateracją sferyczną ) to metoda określania położenia ruchomego pojazdu lub nieruchomego punktu w przestrzeni przy użyciu wielu zakresów ( odległości ) między pojazdem/punktem a wieloma oddzielonymi przestrzennie znanymi lokalizacjami ( często określane jako „stacje”). Fale energii mogą być zaangażowane w określanie zasięgu, ale nie są wymagane.

Multilateracja rzeczywistego zakresu jest zarówno tematem matematycznym, jak i techniką stosowaną stosowaną w kilku dziedzinach. Praktyczne zastosowanie związane z ustaloną lokalizacją występuje w geodezji . Aplikacje związane z lokalizacją pojazdu nazywane są nawigacją , gdy osoby/sprzęt na pokładzie są informowane o jego lokalizacji, a nazywane są inwigilacją , gdy jednostki znajdujące się poza pojazdem są informowane o lokalizacji pojazdu.

Dwa zakresy nachylenia z dwóch znanych lokalizacji mogą być wykorzystane do zlokalizowania trzeciego punktu w dwuwymiarowej przestrzeni kartezjańskiej (płaszczyźnie), co jest często stosowaną techniką (np. w geodezji). Podobnie dwa zakresy sferyczne mogą być użyte do zlokalizowania punktu na kuli, co jest fundamentalną koncepcją starożytnej dyscypliny nawigacji na niebie — określanej jako problem przecięcia wysokości . Ponadto, jeśli dostępnych jest więcej niż minimalna liczba zakresów, dobrą praktyką jest ich wykorzystanie. Ten artykuł dotyczy ogólnego problemu określania pozycji przy użyciu wielu zakresów.

W geometrii dwuwymiarowej wiadomo, że jeśli punkt leży na dwóch okręgach, to środki okręgów i dwa promienie dostarczają informacji wystarczających do zawężenia możliwych lokalizacji do dwóch — z których jedno jest rozwiązaniem pożądanym, a drugie rozwiązaniem niejednoznaczne rozwiązanie. Dodatkowe informacje często zawężają możliwości do unikalnej lokalizacji. W geometrii trójwymiarowej, gdy wiadomo, że punkt leży na powierzchniach trzech sfer, to środki trzech sfer wraz z ich promieniami również dostarczają informacji wystarczających do zawężenia możliwych lokalizacji do nie więcej niż dwóch (chyba że środki leżą na linii prostej).

Multilaterację rzeczywistego zasięgu można porównać do częściej spotykanej multilateracji pseudozakresowej , która wykorzystuje różnice w zakresie do zlokalizowania (zwykle ruchomego) punktu. Multilateracja pseudozakresu jest prawie zawsze realizowana poprzez pomiar czasów nadejścia (TOA) fal energii. Multilaterację w rzeczywistym zakresie można również przeciwstawić triangulacji , która obejmuje pomiar kątów .

Terminologia

Nie ma akceptowanego ani szeroko stosowanego ogólnego terminu na to, co nazywa się tutaj multilateracją rzeczywistego zasięgu . Wybrano tę nazwę, ponieważ: (a) jest dokładnym opisem i częściowo znaną terminologią ( w tym kontekście często używa się multilateracji ); (b) unika określania liczby zaangażowanych zakresów (jak np. range-range ; (c) unika sugerowania zastosowania (jak np. nawigacja DME/DME lub trilateracja ) oraz (d) i unika pomylenia z bardziej wspólna multilateracja pseudozakresu .

Uzyskanie zakresów

W przypadku podobnych zasięgów i błędów pomiarowych system nawigacji i nadzoru oparty na multilateracji rzeczywistego zasięgu zapewnia obsługę znacznie większego obszaru 2-D lub objętości 3-D niż systemy oparte na multilateracji pseudo- zakresu . Jednak mierzenie prawdziwych zakresów jest często trudniejsze lub bardziej kosztowne niż mierzenie pseudozakresów. W przypadku odległości do kilku mil i stałych lokalizacji rzeczywisty zasięg można zmierzyć ręcznie. Robiono to w geodezji od kilku tysięcy lat – np. za pomocą lin i łańcuchów.

W przypadku dłuższych odległości i/lub poruszających się pojazdów zazwyczaj potrzebny jest system radiowo-radarowy. Technologia ta została po raz pierwszy opracowana około 1940 roku w połączeniu z radarem. Od tego czasu zastosowano trzy metody:

Dwukierunkowy pomiar zasięgu, jedna strona aktywna - Jest to metoda stosowana przez tradycyjne radary (czasami nazywane radarami pierwotnymi ) do określania zasięgu niewspółpracującego celu, a obecnie używana przez dalmierze laserowe . Jego główne ograniczenia polegają na tym, że: (a) cel nie identyfikuje się, aw sytuacji wielu celów może wystąpić błędne przypisanie zwrotu; (b) sygnał zwrotny jest tłumiony (w stosunku do sygnału nadawanego) o czwartą potęgę zasięgu pojazdu-stacji (tak więc dla odległości dziesiątek mil lub więcej stacje generalnie wymagają nadajników dużej mocy i/lub dużych/czułych anteny); oraz (c) wiele systemów wykorzystuje propagację w linii wzroku, co ogranicza ich zasięg do mniej niż 20 mil, gdy obie strony znajdują się na podobnych wysokościach nad poziomem morza.
Dwukierunkowy pomiar zasięgu, obie strony aktywne - podobno ta metoda została po raz pierwszy zastosowana do nawigacji przez system naprowadzania samolotu Y-Gerät, wprowadzony w 1941 roku przez Luftwaffe. Jest obecnie używany na całym świecie w kontroli ruchu lotniczego – np. wtórnym i nawigacji DME/DME. Wymaga, aby obie strony miały zarówno nadajniki, jak i odbiorniki, i może wymagać rozwiązania problemów związanych z zakłóceniami.
Jednokierunkowy pomiar zasięgu – Czas przelotu (TOF) energii elektromagnetycznej między wieloma stacjami a pojazdem jest mierzony na podstawie transmisji przez jedną stronę i odbioru przez drugą. Jest to ostatnio opracowana metoda, którą umożliwił rozwój zegarów atomowych ; wymaga, aby pojazd (użytkownik) i stacje posiadały zsynchronizowane zegary. Zostało to pomyślnie zademonstrowane (eksperymentalnie) z Loran-C i GPS.

Metody rozwiązania

multilateracji rzeczywistego zasięgu można podzielić na podstawie

wymiar przestrzeni problemowej (na ogół dwa lub trzy),
geometria przestrzeni problemowej (ogólnie kartezjańska lub sferyczna) oraz
obecność zbędnych pomiarów (więcej niż wymiar przestrzeni problemowej).

Każdy algorytm multilateracji pseudozakresu może być wyspecjalizowany do użytku z multilateracją prawdziwego zasięgu.

Dwa wymiary kartezjańskie, dwa zmierzone zakresy nachylenia (trilateracja)

Ryc. 1 Scenariusz 2-D kartezjańskiej multilateracji rzeczywistego zakresu (trilateracji). C1 i C2 to środki okręgów o

znanej

. P

\

punktem, którego

współrzędne są

na podstawie i zakresów i

displaystyle r_ {1}

i

displaystyle r_ {} 2}}

.

Rozwiązanie analityczne jest prawdopodobnie znane od ponad 1000 lat i jest podane w kilku tekstach. Co więcej, można łatwo dostosować algorytmy do trójwymiarowej przestrzeni kartezjańskiej.

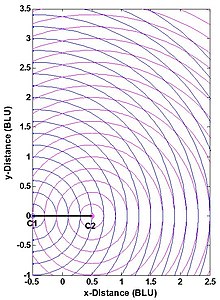
Najprostszy algorytm wykorzystuje geometrię analityczną i układ współrzędnych oparty na stacji. Rozważmy zatem środki okręgów (lub stacje) $,$ i C2 na ryc. 1 które mają znane współrzędne (np. zostały już zbadane), a zatem których separacja jest znana. Rysunek „strona” zawiera C1 i C2 . Jeżeli trzeci „punkt zainteresowania” P (np. pojazd lub inny punkt do zbadania) znajduje się w nieznanym punkcie ${\ Displaystyle (x, y)}$ , to twierdzenie Pitagorasa daje wyniki

{\ Displaystyle {\ rozpocząć {wyrównane} r_ {1} ^ {2} i = x ^ {2} + y ^ { 2}\\[4pt]r_{2}^{2}&=(Ux)^{2}+y^{2}\end{wyrównane}}}

Zatem,

${\ Displaystyle {\ rozpocząć {wyrównane} x & = {\ Frac {r_ {1} ^ {2} -r_ {2} }^{2}+U^{2}}{2U}}\\[4pt]y&=\pm {\sqrt {r_{1}^{2}-x^{2}}}\end{wyrównane} }}$

()

Zauważ, że $wartości$ (tj. rozwiązanie jest niejednoznaczne); zazwyczaj nie stanowi to problemu.

Chociaż istnieje wiele ulepszeń, równanie 1 jest najbardziej podstawową relacją multilateracji w rzeczywistym zakresie. Przykładem jej zastosowania jest nawigacja samolotowa DME/DME oraz trilateracyjna metoda geodezyjna. Podczas II wojny światowej Oboe i podczas wojny koreańskiej SHORAN stosował tę samą zasadę do naprowadzania samolotów na podstawie zmierzonych odległości do dwóch stacji naziemnych. SHORAN był później używany do poszukiwań ropy naftowej na morzu i do pomiarów lotniczych. Australijski system badań lotniczych Aerodist wykorzystywał dwuwymiarową kartezjańską multilaterację rzeczywistego zasięgu. Ten dwuwymiarowy scenariusz jest na tyle ważny, że termin trilateracja jest często stosowana we wszystkich zastosowaniach obejmujących znane pomiary linii bazowej i dwóch zakresów.

Linia bazowa zawierająca środki okręgów jest linią symetrii. Poprawne i niejednoznaczne rozwiązania są prostopadłe i jednakowo oddalone od (po przeciwnych stronach) linii bazowej. Zwykle niejednoznaczne rozwiązanie jest łatwe do zidentyfikowania. Na przykład, jeśli P jest pojazdem, każdy ruch w kierunku lub od linii podstawowej będzie przeciwny do ruchu niejednoznacznego rozwiązania; w związku z tym wystarczy przybliżony pomiar kursu pojazdu. Drugi przykład: geodeci doskonale wiedzą, po której stronie linii bazowej leży P. Trzeci przykład: w zastosowaniach, w których P to statek powietrzny, a C1 i C2 są na ziemi, niejednoznaczne rozwiązanie jest zwykle pod ziemią.

W razie potrzeby kąty wewnętrzne trójkąta C1-C2-P można znaleźć za pomocą twierdzenia trygonometrycznego cosinusów . Ponadto, jeśli to konieczne, współrzędne P mogą być wyrażone w drugim, lepiej znanym układzie współrzędnych — np. układzie Universal Transverse Mercator (UTM) — pod warunkiem, że współrzędne C1 i C2 są znane w tym drugim układzie. Oba są często wykonywane w geodezji, gdy stosowana jest metoda trilateracji. ustaleniu współrzędnych P , linie C1-P i C2-P mogą być używane jako nowe linie bazowe i dodatkowe badane punkty. W ten sposób duże obszary lub odległości można badać na podstawie wielu mniejszych trójkątów — zwanych trawersami .

Domniemanym założeniem, że powyższe równanie jest prawdziwe, jest to, że i odnoszą się do tej samej pozycji $}$ r ${1}$ Gdy P jest pojazdem, to zazwyczaj i $displaystyle$ $r_ {2}}$ muszą być mierzone w ramach tolerancji synchronizacji, która zależy od prędkości pojazdu i dopuszczalnego błędu położenia Alternatywnie, ruch pojazdu między pomiarami odległości może być uwzględniony, często przez zliczanie martwe.

Możliwe jest również rozwiązanie trygonometryczne (przypadek side-side-side). Możliwe jest również rozwiązanie wykorzystujące grafikę. Rozwiązanie graficzne jest czasami stosowane podczas nawigacji w czasie rzeczywistym, jako nakładka na mapę.

Trzy wymiary kartezjańskie, trzy zmierzone zakresy nachylenia

Ryc. 2 Scenariusz multilateracji 3-D True-Range. C1, C2 i C3 to znane środki sfer na płaszczyźnie x,y. P jest punktem, którego współrzędne (x,y,z) są pożądane na podstawie jego zakresów do C1, C2 i C3.

3-D Tri lateration ogranicza liczbę potencjalnych pozycji do dwóch (tutaj A lub B)

Istnieje wiele algorytmów, które bezpośrednio rozwiązują trójwymiarowy kartezjański problem multilateracji rzeczywistego zasięgu (tj. w formie zamkniętej) – np. Fang. Ponadto można przyjąć algorytmy w postaci zamkniętej opracowane dla multilateracji pseudozakresowej . Algorytm Bancrofta (zaadaptowany) wykorzystuje wektory, co w niektórych sytuacjach jest zaletą.

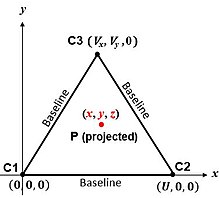
Najprostszy algorytm odpowiada środkom sfer na ryc. 2. Figura „strona” to płaszczyzna zawierająca C1 , C2 i C3 . Jeśli P jest „punktem zainteresowania” (np. pojazdem) w punkcie ${\ Displaystyle (x, y, z)}$ , to twierdzenie Pitagorasa daje zakresy nachylenia między P a środkami sfer: ( x , y , z )

{\ Displaystyle {\ rozpocząć {wyrównane} r_ {1} ^ {2} & = x ^ {2} + y ^ {2} + z ^ {2} \\ [4pt] r_ {2} ^ {2} i =(xU)^{2}+y^{2}+z^{2}\\[4pt]r_{3}^{2}&=(x-V_{x})^{2}+(y -V_{y})^{2}+z^{2}\end{wyrównane}}}

Zatem współrzędne P to:

${\ Displaystyle {\ rozpocząć {wyrównane} x & = {\ Frac {r_ {1} ^ {2} -r_ {2} ^ {2} + U ^ {2}} {2U}} \\ [4pt] y & = {\frac {r_{1}^{2}-r_{3}^{2}+V_{x}^{2}+V_{y}^{2}-2V_{x}x}{2V_{y }}}\\[4pt]z&=\pm {\sqrt {r_{1}^{2}-x^{2}-y^{2}}}\end{wyrównane}}}$

()

Płaszczyzna zawierająca środki sfer jest płaszczyzną symetrii. Poprawne i niejednoznaczne rozwiązania są prostopadłe do niej i jednakowo od niej oddalone, po przeciwnych stronach.

Wiele zastosowań trójwymiarowej multilateracji rzeczywistego zakresu obejmuje krótkie zakresy — np. produkcja precyzyjna. Integracja pomiaru zasięgu z trzech lub więcej radarów (np. ERAM FAA ) to trójwymiarowa aplikacja do obserwacji samolotów. Trójwymiarowa multilateracja rzeczywistego zasięgu została wykorzystana eksperymentalnie z satelitami GPS do nawigacji lotniczej. Wymóg wyposażenia statku powietrznego w zegar atomowy wyklucza jego ogólne użycie. Jednak wspomaganie zegara odbiornika GPS jest obszarem aktywnych badań, w tym wspomagania przez sieć. W związku z tym wnioski mogą ulec zmianie. Organizacja Międzynarodowego Lotnictwa Cywilnego oceniła trójwymiarową multilaterację rzeczywistego zasięgu jako system lądowania samolotu, ale inna technika okazała się bardziej wydajna. Dokładny pomiar wysokości samolotu podczas podejścia i lądowania wymaga wielu stacji naziemnych wzdłuż toru lotu.

Dwa wymiary sferyczne, dwa lub więcej mierzonych zakresów sferycznych

Rys. 3 Przykład problemu przecięcia wysokości nawigacji na niebie (linie pozycji są zniekształcone przez odwzorowanie mapy)

Jest to klasyczny problem nawigacji na niebie (lub astronomii), nazywany problemem przecięcia wysokości (ryc. 3). Jest to ekwiwalent geometrii sferycznej metody trilateracji geodezji (chociaż odległości są na ogół znacznie większe). Rozwiązanie na morzu (niekoniecznie obejmujące słońce i księżyc) było możliwe dzięki chronometrowi morskiemu (wprowadzonemu w 1761 r.) i odkryciu „linii położenia” (LOP) w 1837 r. Metoda rozwiązania jest obecnie najczęściej nauczana na uniwersytetach ( np. Akademia Marynarki Wojennej Stanów Zjednoczonych) wykorzystuje sferyczną trygonometrię do rozwiązania ukośnego trójkąta sferycznego w oparciu o sekstansowe pomiary „wysokości” dwóch ciał niebieskich. Ten problem można również rozwiązać za pomocą analizy wektorowej. stosowano techniki graficzne – np. metodę przechwytywania . Mogą one pomieścić więcej niż dwie zmierzone „wysokości”. Ze względu na trudność dokonywania pomiarów na morzu, często zaleca się od 3 do 5 „wysokości”.

Ponieważ Ziemię lepiej modeluje się jako elipsoidę obrotową niż kulę, w nowoczesnych implementacjach można zastosować techniki iteracyjne. W samolotach i pociskach latających na dużych wysokościach podsystem nawigacji kosmicznej jest często zintegrowany z podsystemem nawigacji inercyjnej w celu wykonywania zautomatyzowanej nawigacji - np. US Air Force SR-71 Blackbird i B-2 Spirit .

Choć pomyślany jako „sferyczny” system multilateracji pseudozakresu, Loran-C był również używany jako „sferyczny” system multilateracji prawdziwego zasięgu przez dobrze wyposażonych użytkowników (np. Kanadyjska Służba Hydrograficzna). Umożliwiło to znaczne zwiększenie zasięgu triady stacji Loran-C (np. podwojenie lub potrojenie) oraz zmniejszenie minimalnej liczby dostępnych nadajników z trzech do dwóch. We współczesnym lotnictwie częściej mierzone są zasięgi skośne niż sferyczne; jednakże, gdy znana jest wysokość samolotu, zakresy nachylenia są łatwo konwertowane na zakresy sferyczne.

Nadmiarowe pomiary zasięgu

Gdy dostępnych jest więcej pomiarów zasięgu niż wymiarów problemowych, albo z tych samych stacji C1 i C2 (lub C1 , C2 i C3 ), albo z dodatkowych stacji, naliczają się przynajmniej następujące korzyści:

„Złe” pomiary można zidentyfikować i odrzucić
Niejednoznaczne rozwiązania mogą być identyfikowane automatycznie (tj. bez udziału człowieka) – wymaga dodatkowej stacji
Błędy w „dobrych” pomiarach można uśrednić, zmniejszając ich wpływ.

Iteracyjny algorytm Gaussa-Newtona do rozwiązywania nieliniowych problemów najmniejszych kwadratów (NLLS) jest generalnie preferowany, gdy jest więcej „dobrych” pomiarów niż niezbędne minimum. Ważną zaletą metody Gaussa-Newtona w porównaniu z wieloma algorytmami w postaci zamkniętej jest to, że traktuje ona błędy zakresu liniowo, co często jest ich naturą, zmniejszając w ten sposób wpływ błędów zakresu poprzez uśrednianie. Metodę Gaussa-Newtona można również zastosować przy minimalnej liczbie mierzonych zakresów. Ponieważ jest iteracyjna, metoda Gaussa-Newtona wymaga wstępnego oszacowania rozwiązania.

W trójwymiarowej przestrzeni kartezjańskiej czwarta sfera eliminuje niejednoznaczne rozwiązanie, które występuje w przypadku trzech zakresów, pod warunkiem, że jej środek nie jest współpłaszczyznowy z pierwszymi trzema. W dwuwymiarowej przestrzeni kartezjańskiej lub sferycznej trzeci okrąg eliminuje niejednoznaczne rozwiązanie, które występuje w przypadku dwóch zakresów, pod warunkiem, że jego środek nie jest współliniowy z dwoma pierwszymi.

Aplikacja jednorazowa a aplikacja powtarzalna

Ten artykuł w dużej mierze opisuje „jednorazowe” zastosowanie techniki multilateracji rzeczywistego zasięgu, która jest najbardziej podstawowym zastosowaniem tej techniki. W odniesieniu do fig. 1, cechą charakterystyczną sytuacji „jednorazowych” jest to, że punkt P i co najmniej jeden z C1 i C2 zmieniają się od jednego zastosowania techniki multilateracji rzeczywistego zasięgu do następnego. Jest to odpowiednie do pomiarów geodezyjnych, nawigacji na niebie z wykorzystaniem obserwacji ręcznych oraz nawigacji DME/DME niektórych statków powietrznych.

Jednak w innych sytuacjach technika multilateracji w rzeczywistym zakresie jest stosowana w sposób powtarzalny (zasadniczo w sposób ciągły). W takich sytuacjach C1 i C2 (i być może Cn, n = 3,4,... ) pozostają stałe, a P to ten sam pojazd Przykładowe zastosowania (i wybrane odstępy między pomiarami) to: obserwacja wielu radarów statków powietrznych (5 i 12 sekund, w zależności od zasięgu pokrycia radarowego), pomiary lotnicze, nawigacja Loran-C z bardzo dokładnym zegarem użytkownika (około 0,1 sekundy) oraz niektóre nawigacja DME/DME samolotu (około 0,1 sekundy). Ogólnie rzecz biorąc, implementacje do powtarzalnego użytku: a) wykorzystują algorytm „śledzący” (oprócz algorytmu rozwiązania multilateracji), który umożliwia porównanie i uśrednienie pomiarów zebranych w różnym czasie; oraz (b) wykorzystują iteracyjny algorytm rozwiązania, ponieważ (b1) dopuszczają różne liczby pomiarów (w tym pomiary redundantne) oraz (b2) z natury mają wstępne przypuszczenie za każdym razem, gdy algorytm rozwiązania jest wywoływany.

Hybrydowe systemy multilateracyjne

Hybrydowe systemy multilateracyjne – takie, które nie są ani systemami prawdziwego zasięgu, ani pseudo-zakresu – są również możliwe. Na przykład na ryc. 1, jeśli środki okręgów są przesunięte w lewo, tak że C1 znajduje się w punkcie ${\ Displaystyle x_ {1} ^ {\ pierwsza} = - { \tfrac {1}{2}}U,y_{1}^{\prime }=0}$ i C2 jest w punkcie ${\ Displaystyle x_ {2} ^ {\ pierwsza} = {\ tfrac {1}{2}} U, y_ {2} ^ {\ pierwsza} = 0}$ to punkt zainteresowania P znajduje się w

{\ Displaystyle {\ rozpocząć {wyrównane} x ^ {\ pierwsza} & = {\ Frac {(r_ {1} ^ {\ pierwsza} + r_ {2} ^ {\ pierwsza}) (r_ {1} ^ {\prime}-r_{2}^{\prime})}{2U}}\\[4pt]y^{\prime}&=\pm {\frac {{\sqrt {(r_{1}^{ \prime }+r_{2}^{\prime })^{2}-U^{2}}}{\sqrt {U^{2}-(r_{1}^{\prime }-r_{2 }^{\prime})^{2}}}}{2U}}\end{wyrównane}}}

$r_ {1} ^ {\ pierwsza}}$ rozwiązania wyraźnie zależy od sumy i różnicy 1 $displaystyle$ i nie $„$ $-rozwiązania$ ” od . Można go zaimplementować jako system multilateracji rzeczywistego zasięgu, mierząc i ${\ displaystyle r_ {1} ^ {\ pierwsza}$ } ${\ displaystyle r_ {2} ^ {\ pierwsza}}$ .

Jednak można go również zaimplementować jako hybrydowy system multilateracji, mierząc ${\ Displaystyle r_ {1} ^ {\ pierwsza} + r_ {2} ^ {\ pierwsza}}$ i $dwoma$ przy użyciu innego sprzętu - np. Do obserwacji przez multistatyczny z jednym odbiornikami (zamiast dwóch radarów monostatycznych ). Chociaż wyeliminowanie jednego nadajnika jest korzystne, istnieje równoważący go „koszt”: tolerancja synchronizacji dla dwóch stacji staje się zależna od prędkości propagacji (zwykle prędkości światła), a nie od prędkości punktu P , w celu dokładnego pomiaru oba ${\ Displaystyle r_ {1} ^ {\ pierwsza} \ pm r_ {2} ^ {\ pierwsza}}$ .

Hybrydowe systemy multilateracji, które nie zostały wdrożone operacyjnie, zostały zbadane pod kątem nadzoru statków powietrznych w pobliżu lotnisk oraz jako zapasowy system nawigacji GPS dla lotnictwa.

Obliczenia wstępne i końcowe

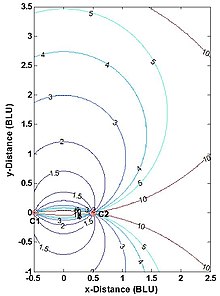
Ryc. 4 Dwuwymiarowe pomiary odległości systemu multilateracji (trilateracji) w rzeczywistym zakresie

Dokładność pozycji systemu multilateracji rzeczywistego zakresu - np. Dokładność współrzędnych $punktu$ P na ryc zakresu dokładność pomiaru oraz (2) stosunek geometryczny P do stacji systemu C1 i C2 . Można to zrozumieć na podstawie ryc. 4. Dwie stacje są pokazane jako kropki, a BLU oznacza jednostki podstawowe. (Wzorzec pomiaru jest symetryczny zarówno względem linii bazowej, jak i prostopadłej dwusiecznej linii bazowej i jest obcięty na rysunku). Jak zwykle, przyjmuje się, że błędy pomiaru poszczególnych zakresów są niezależne od zakresu, statystycznie niezależne i mają identyczny rozkład. To rozsądne założenie oddziela wpływ geometrii stacji użytkownika i błędów pomiaru zasięgu na błąd obliczonych współrzędnych P. ${\ Displaystyle (x, y)}$ . W tym przypadku geometria pomiaru to po prostu kąt, pod którym przecinają się dwa okręgi — lub równoważnie kąt między liniami P-C1 i P-C2 . Gdy punkt P- nie leży na okręgu, błąd jego położenia jest w przybliżeniu proporcjonalny do obszaru ograniczonego dwoma najbliższymi niebieskimi i dwoma najbliższymi purpurowymi okręgami.

Bez zbędnych pomiarów system multilateracji rzeczywistego zakresu nie może być dokładniejszy niż pomiary zakresu, ale może być znacznie mniej dokładny, jeśli geometria pomiaru nie zostanie wybrana prawidłowo. W związku z tym niektóre aplikacje nakładają ograniczenia na położenie punktu P. W przypadku sytuacji kartezjańskiej 2-D (trilateracji) ograniczenia te przybierają jedną z dwóch równoważnych postaci:

Dopuszczalny kąt wewnętrzny w punkcie P między liniami P-C1 i P-C2 : Ideałem jest kąt prosty, który występuje w odległości od linii podstawowej wynoszącej połowę lub mniej długości linii podstawowej; można określić maksymalne dopuszczalne odchylenia od idealnych 90 stopni.
Poziome rozcieńczenie precyzji (HDOP), które mnoży błąd zakresu przy określaniu błędu pozycji: dla dwóch wymiarów idealny (minimalny) HDOP to pierwiastek kwadratowy z 2 ( 2 ≈ 1,414 {\ $sqrt {2}}} \około 1,414}$ ), co występuje, gdy kąt między P-C1 i P-C2 wynosi 90 stopni; można określić maksymalną dopuszczalną wartość HDOP. (Tutaj równe HDOP to po prostu zbiór punktów na ryc. 4 o tym samym kącie przecięcia.)

Ryc. 5 Kontury HDOP dla dwuwymiarowego systemu multilateracji (trilateracji) w rzeczywistym zakresie

Planowanie multilateracyjnego systemu nawigacji lub nadzoru w rzeczywistym zasięgu często obejmuje analizę rozmycia precyzji (DOP) w celu podjęcia decyzji dotyczących liczby i lokalizacji stacji oraz obszaru usług systemu (dwa wymiary) lub wielkości usług (trzy wymiary). Ryc. 5 przedstawia poziome DOP (HDOP) dla 2-D, dwustanowiskowego systemu multilateracji rzeczywistego zasięgu. HDOP jest nieskończony wzdłuż linii bazowej i jej przedłużeń, ponieważ w rzeczywistości mierzony jest tylko jeden z dwóch wymiarów. Użytkownik takiego systemu powinien znajdować się mniej więcej poza linią bazową iw zakresie zależnym od aplikacji. Na przykład w przypadku poprawek nawigacyjnych DME/DME przez samolot maksymalny HDOP dozwolony przez amerykańską FAA jest dwukrotnością minimalnej możliwej wartości lub 2,828, co ogranicza maksymalny zakres użytkowania (który występuje wzdłuż dwusiecznej linii bazowej) do 1,866-krotności długości linii bazowej . (Płaszczyzna zawierająca dwie stacje naziemne DME i samolot nie jest ściśle pozioma, ale zwykle jest prawie taka). Podobnie geodeci wybierają punkt P na ryc. 1 tak, że C1-C2-P z grubsza tworzą trójkąt równoboczny (gdzie HDOP = 1,633).

Błędy w badaniach trójlateracyjnych są omówione w kilku dokumentach. Ogólnie rzecz biorąc, nacisk kładzie się na skutki błędów pomiaru zakresu, a nie na skutki błędów numerycznych algorytmu.

Aplikacje

Geodezja metodą trilateracji
Pomiary lotnicze
Geodezja archeologii morskiej
Nawigacja samolotowa DME/DME RNAV
Integracja wielu radarów (np. FAA ERAM )
Niebiańska nawigacja przy użyciu metody przecięcia wysokości
Metoda przecięcia — graficzne rozwiązanie problemu przecięcia wysokości
Kalibracja interferometrów laserowych
SHORAN , Oboe , Gee-H — Systemy naprowadzania samolotów opracowane do bombardowania „na ślepo”
JTIDS ( Joint Tactical Information Distribution System ) - system USA / NATO, który (między innymi) lokalizuje uczestników w sieci za pomocą zakresów między uczestnikami
USAF SR-71 Blackbird — wykorzystuje nawigację astro-inercyjną
USAF B-2 Spirit — wykorzystuje nawigację astro-inercyjną
Eksperymentalna technika Loran-C

Zalety i wady nawigacji samochodowej i nadzoru

Systemy nawigacji i nadzoru zwykle obejmują pojazdy i wymagają, aby jednostka rządowa lub inna organizacja rozmieściła wiele stacji, które wykorzystują technologię radiową (tj. wykorzystują fale elektromagnetyczne). W poniższej tabeli przedstawiono zalety i wady zastosowania multilateracji rzeczywistego zasięgu w takim systemie.

Zalety	Niedogodności
Lokalizacje stacji są elastyczne; mogą być umieszczone centralnie lub peryferyjnie Dokładność spada powoli wraz z odległością od stacji (ogólnie lepsza niż multilateracja pseudoodległości) Wymaga o jedną stację mniej niż system multilateracji pseudozakresu Synchronizacja stacji nie jest wymagająca (w oparciu o prędkość punktu szczególnego i może być adresowana przez zliczanie martwe )	Często od użytkownika wymagane jest posiadanie zarówno nadajnika, jak i odbiornika Dokładność systemu współpracy jest wrażliwa na błąd obrotu sprzętu Nie można używać do niewidzialnej obserwacji Obserwacja niewspółpracująca wiąże się z utratą ścieżki do czwartej potęgi odległości

Multilateracja rzeczywistego zasięgu jest często porównywana z multilateracją (pseudozakresu), ponieważ obie wymagają pewnej formy zakresów użytkownika do wielu stacji. Złożoność i koszt wyposażenia użytkownika jest prawdopodobnie najważniejszym czynnikiem ograniczającym wykorzystanie multilateracji rzeczywistego zasięgu do nawigacji i nadzoru pojazdów. Niektóre zastosowania nie są pierwotnym celem wdrożenia systemu – np. nawigacja samolotowa DME/DME.

Zobacz też

Problem geometrii odległości , podobna technika zastosowana do cząsteczek
Niebiańska nawigacja — starożytna technika nawigacji oparta na ciałach niebieskich
Sprzęt do pomiaru odległości (DME) — system używany do pomiaru odległości między statkiem powietrznym a stacją naziemną
Odległość euklidesowa
Metoda przechwytywania — technika graficzna stosowana w nawigacji na niebie
Dalmierz laserowy
Multilateracja — odnosi się do multilateracji pseudozakresu
Dalmierz — systemy używane do pomiaru odległości między dwoma punktami na ziemi
Resekcja (orientacja)
SHORAN — opracowany jako system nawigacji samolotów wojskowych, później używany do celów cywilnych
Geodezja
Tellurometr — pierwszy elektroniczny dalmierz mikrofalowy
Triangulacja – Metoda geodezyjna oparta na pomiarze kątów

Linki zewnętrzne

stackexchange.com , Implementacja PHP / Python