Podatność elektryczna

W elektryczności ( elektromagnetyzmie ) podatność elektryczna ( $w$ Susceptibilis " receptive " ) jest bezwymiarową stałą proporcjonalności, która wskazuje stopień polaryzacji materiału dielektrycznego reakcja na przyłożone pole elektryczne . Im większa podatność elektryczna, tym większa zdolność materiału do polaryzacji w odpowiedzi na pole, a tym samym do zmniejszenia całkowitego pola elektrycznego wewnątrz materiału (i magazynowania energii). W ten sposób podatność elektryczna wpływa na przenikalność elektryczną materiału, a tym samym wpływa na wiele innych zjawisk w tym ośrodku, od pojemności kondensatorów po prędkość światła .

Definicja dielektryków liniowych

Jeśli materiał dielektryczny jest dielektrykiem liniowym, to podatność elektryczną definiuje się jako stałą proporcjonalności (która może być macierzą) odnoszącą pole elektryczne E do indukowanej gęstości polaryzacji dielektrycznej P takiej, że

{\ Displaystyle \ mathbf {P} = \ varepsilon _ {0} \ chi _ {\ tekst {e}} {\ mathbf {E}},}

Gdzie

${\ Displaystyle \ mathbf {P}}$ to gęstość polaryzacji;
${\ Displaystyle \ varepsilon _ {0}}$ to przenikalność elektryczna wolnej przestrzeni (stała elektryczna);
${\ Displaystyle \ chi _ {\ tekst {e}}}$ to podatność elektryczna;
${\ Displaystyle \ mathbf {E}}$ jest polem elektrycznym.

W materiałach, w których podatność jest anizotropowa (różna w zależności od kierunku), podatność jest reprezentowana jako macierz znana jako tensor podatności. Wiele dielektryków liniowych jest izotropowych, ale mimo to materiał może wykazywać zachowanie zarówno liniowe, jak i anizotropowe, lub materiał może być nieliniowy, ale izotropowy. Anizotropowa, ale liniowa podatność jest powszechna w wielu kryształach.

Podatność jest związana z jego względną przenikalnością (stała dielektryczna) przez ${\ displaystyle \ varepsilon _ {\ textrm {r}}}$

{\ Displaystyle \ chi _ {\ tekst {e}} \ = \ varepsilon _ {\ tekst {r}} -1}

więc w przypadku próżni

{\ Displaystyle \ chi _ {\ tekst {e}} \ = 0.}

Jednocześnie przemieszczenie elektryczne D jest powiązane z gęstością polaryzacji P następującą zależnością:

{\ Displaystyle \ mathbf {D} \ = \ \ varepsilon _ {0} \ mathbf {E} + \ mathbf {P } \ =\ \varepsilon _{0}(1+\chi _{\text{e}})\mathbf {E} \ =\ \varepsilon _{\text{r}}\varepsilon _{0}\mathbf {E} \ =\ \varepsilon \mathbf {E} }

Gdzie

${\ Displaystyle \ varepsilon \ = \ \ varepsilon _ {\ tekst {r}} \ varepsilon _ {0}}$
${\ Displaystyle \ varepsilon _ {\ tekst {r}} \ = \ (1 + \ chi _ {\ tekst {e}})}$

Polaryzowalność molekularna

Podobny parametr istnieje, aby powiązać wielkość indukowanego momentu dipolowego p pojedynczej cząsteczki z lokalnym polem elektrycznym E , które indukowało dipol. Tym parametrem jest polaryzowalność molekularna ( α ), a moment dipolowy wynikający z lokalnego pola elektrycznego E _local wyraża się wzorem:

{\ Displaystyle \ mathbf {p} = \ varepsilon _ {0} \ alfa \ mathbf {E _ {\ tekst {lokalny}}}}

Wprowadza to jednak komplikacje, ponieważ lokalnie pole może znacznie różnić się od ogólnego zastosowanego pola. Mamy:

{\ Displaystyle \ mathbf {P} = N \ mathbf {p} = N \ varepsilon _ {0} \ alfa \ mathbf {E} _ {\ tekst {lokalny}}, }

gdzie P to polaryzacja na jednostkę objętości, a N to liczba cząsteczek na jednostkę objętości, które przyczyniają się do polaryzacji. Zatem, jeśli lokalne pole elektryczne jest równoległe do otaczającego pola elektrycznego, mamy:

{\ Displaystyle \ chi _ {\ tekst {e}} \ mathbf {E} = N \ alfa \ mathbf {E} _ {\ tekst {lokalny}}}

Zatem tylko wtedy, gdy pole lokalne jest równe polu otoczenia, możemy napisać:

{\ Displaystyle \ chi _ {\ tekst {e}} = N \ alfa.}

W przeciwnym razie należałoby znaleźć związek między polem lokalnym a polem makroskopowym. W niektórych materiałach obowiązuje i brzmi relacja Clausiusa – Mossottiego

{\ Displaystyle {\ Frac {\ chi _ {\ tekst {e}}} {3+ \ chi _ {\ tekst {e}}}} = {\ frac {N \ alfa} {3}}.}

Niejasność w definicji

Definicja polaryzowalności molekularnej zależy od autora. W powyższej definicji

{\ Displaystyle \ mathbf {p} = \ varepsilon _ {0} \ alfa \ mathbf {E_ {\ tekst {lokalny}}}}

}

polaryzowalność

p

i są w jednostkach molekularna ma wymiar objętości (m ³ ). Inną definicją byłoby zachowanie jednostek SI i zintegrowanie w :

displaystyle

\ varepsilon _ {0}}

\

{\ Displaystyle \ mathbf {p} = \ alfa \ mathbf {E_ {\ tekst {lokalny}}}.}

W tej drugiej definicji polaryzowalność miałaby jednostkę SI Cm2 ^/ V. Istnieje jeszcze inna definicja, w której $}$ są wyrażane w systemie cgs i $nadal$ są definiowane jako $displaystyle p$

{\ Displaystyle \ mathbf {p} = \ alfa \ mathbf {E_ {\ tekst {lokalny}}}.}

Użycie $,$ cgs daje $objętości$ jak w pierwszej definicji, ale o wartości niższej

Podatność nieliniowa

W wielu materiałach polaryzowalność zaczyna się nasycać przy dużych wartościach pola elektrycznego. To nasycenie można modelować za pomocą nieliniowej podatności . Te podatności są ważne w optyce nieliniowej i prowadzą do efektów, takich jak generowanie drugiej harmonicznej (na przykład używanej do przekształcania światła podczerwonego w światło widzialne w zielonych wskaźnikach laserowych ).

Standardowa definicja podatności nieliniowych w jednostkach SI polega na rozwinięciu Taylora reakcji polaryzacji na pole elektryczne:

{\ Displaystyle P = P_ {0} + \ varepsilon _ {0} \ chi ^ {(1)} E + \ varepsilon _ {0} \ chi ^ {(2)} E ^ {2} + \ varepsilon _ {0 }\chi ^{(3)}E^{3}+\cdots .}

(Z wyjątkiem

}

ferroelektrycznych wbudowana polaryzacja wynosi zero .)

\ Displaystyle \ chi ^ {(1)

składnik podatności, } odpowiada liniowej podatności opisanej powyżej. Chociaż ten pierwszy wyraz jest bezwymiarowy, kolejne nieliniowe podatności mają jednostki

(m / V) n -1

Displaystyle \ chi ^ {(n)}}

\

Nieliniowe podatności można uogólnić na materiały anizotropowe , w których podatność nie jest jednakowa we wszystkich kierunkach. W tych materiałach $staje$ podatność stopnia ( $n + 1$ )

Dyspersja i przyczynowość

Wykres stałej dielektrycznej w funkcji częstotliwości przedstawiający kilka rezonansów i plateau, które wskazują procesy, które reagują na skalę czasu okresu . Pokazuje to, że myślenie o podatności w kategoriach jej transformaty Fouriera jest przydatne.

Ogólnie rzecz biorąc, materiał nie może natychmiast spolaryzować się w odpowiedzi na przyłożone pole, więc bardziej ogólne sformułowanie w funkcji czasu to

{\ Displaystyle \ mathbf {P} (t) = \ varepsilon _ {0} \ int _ {- \ infty} ^ {t} \ chi _ {\ tekst {e}} (tt ') \ mathbf {E} ( t')\,\mathrm {d} t'.}

Oznacza to, że polaryzacja jest splotem pola elektrycznego w poprzednich czasach z podatnością zależną od czasu określoną przez ${\ Displaystyle \ chi _ {\ tekst {e}} (\ Delta t)}$ . ${\ Displaystyle \ chi _ {\ tekst {e}} (\ Delta t) = 0}$ dla Δ $\ styl wyświetlania \Delta t<0}$ . χ $}}\delta (\Delta t)}$ ${\ Displaystyle \ chi _ {\ tekst {e}} (\ Delta t) = \ chi _ {\$ tekst { .

W systemie liniowym wygodniej jest przyjąć transformatę Fouriera i zapisać tę zależność jako funkcję częstotliwości. Dzięki twierdzeniu o splotach całka staje się iloczynem,

{\ Displaystyle \ mathbf {P} (\ omega) = \ varepsilon _ {0} \ chi _ {\ tekst {e}} (\ omega) \ mathbf {E} (\ omega).}

Ma to podobną postać do relacji Clausiusa – Mossottiego :

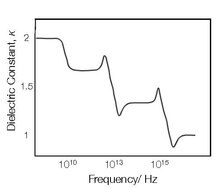
{\ Displaystyle \ mathbf {P} (\ mathbf { r} )=\varepsilon _{0}{\frac {N\alpha (\mathbf {r})}{1-{\frac {1}{3}}N(\mathbf {r})\alpha (\ mathbf {r} )}}\mathbf {E} (\mathbf {r} )=\varepsilon _{0}\chi _{\text{e}}(\mathbf {r} )\mathbf {E} (\ matematyka {r} )}

Ta zależność podatności od częstotliwości prowadzi do zależności przenikalności od częstotliwości. Kształt podatności względem częstotliwości charakteryzuje dyspersyjne materiału.

Co więcej, fakt, że polaryzacja może zależeć tylko od pola elektrycznego w poprzednich czasach (tj. ${\ Displaystyle \ chi _ {\ tekst {e}} (\ Delta t) = 0}$ dla ${\ Displaystyle \ Delta t <0}$ ), konsekwencja przyczynowości , nakłada ograniczenia Kramersa-Kroniga na podatność ${\ Displaystyle \ chi _ {\ tekst {e}} (0)}$ .

Zobacz też