Dipol

Ten artykuł dotyczy zjawiska elektromagnetycznego. W przypadku innych zastosowań zobacz dipol (ujednoznacznienie) .

Pole magnetyczne kuli z północnym biegunem magnetycznym na górze i południowym biegunem magnetycznym na dole. Dla porównania, Ziemia ma południowy biegun magnetyczny w pobliżu północnego bieguna geograficznego i północny biegun magnetyczny w pobliżu bieguna południowego.

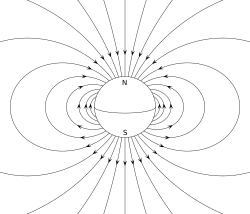
W fizyce dipol (z greckiego δίς (dis) „dwa razy” i πόλος (polos) „oś ” ) jest zjawiskiem elektromagnetycznym , które występuje na dwa sposoby:

• Dipol elektryczny zajmuje się separacją dodatnich i ujemnych ładunków elektrycznych występujących w dowolnym układzie elektromagnetycznym. Prostym przykładem tego systemu jest para ładunków o równej wielkości, ale przeciwnych znakach, oddzielonych zazwyczaj niewielką odległością. (Stały dipol elektryczny nazywany jest elektretem ) .
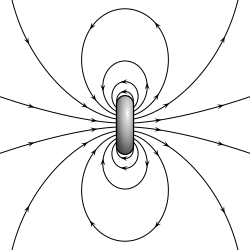
• Dipol magnetyczny to zamknięty obieg systemu prądu elektrycznego . Prostym przykładem jest pojedyncza pętla drutu, przez którą przepływa stały prąd. Przykładem magnesu o stałym magnetycznym momencie dipolowym jest magnes sztabkowy .

Dipole, czy to elektryczne, czy magnetyczne, można scharakteryzować za pomocą ich momentu dipolowego, wielkości wektorowej. W przypadku prostego dipola elektrycznego moment dipolowy jest skierowany od ładunku ujemnego w kierunku ładunku dodatniego i ma wielkość równą sile każdego ładunku pomnożonej przez odległość między ładunkami. ( Dla ścisłości: do określenia momentu dipolowego należy zawsze brać pod uwagę „granicę dipolową”, gdzie np . sposób, że iloczyn pozostaje dodatnią stałą).

Dla magnetycznej (dipolowej) pętli prądowej, magnetyczny moment dipolowy przechodzi przez pętlę (zgodnie z regułą prawego uchwytu ), z wielkością równą prądowi w pętli pomnożonemu przez powierzchnię pętli.

Podobnie jak magnetyczne pętle prądowe, cząstka elektronu i niektóre inne podstawowe cząstki mają magnetyczne momenty dipolowe, ponieważ elektron wytwarza pole magnetyczne identyczne z polem generowanym przez bardzo małą pętlę prądową. Jednak magnetyczny moment dipolowy elektronu nie wynika z pętli prądowej, ale z wewnętrznej właściwości elektronu. Elektron może również mieć elektryczny moment dipolowy, chociaż takiego jeszcze nie zaobserwowano (patrz elektryczny moment dipolowy elektronu ).

Wykres konturowy potencjału elektrostatycznego zorientowanego poziomo dipola elektrycznego o nieskończenie małych rozmiarach. Mocne kolory oznaczają najwyższy i najniższy potencjał (tam, gdzie znajdują się przeciwne ładunki dipola).

Magnes trwały, taki jak magnes sztabkowy, zawdzięcza swój magnetyzm wewnętrznemu magnetycznemu momentowi dipolowemu elektronu. Dwa końce magnesu sztabkowego są określane jako bieguny - nie mylić z monopolami , patrz klasyfikacja poniżej) - i mogą być oznaczone jako „północ” i „południe”. Jeśli chodzi o pole magnetyczne Ziemi, są to odpowiednio bieguny „szukające północy” i „szukające południa”: gdyby magnes był swobodnie zawieszony w polu magnetycznym Ziemi, biegun północny wskazywałby północ i południe- biegun poszukiwawczy wskazywałby na południe. Moment dipolowy magnesu sztabkowego jest skierowany od jego południa magnetycznego do północnego bieguna magnetycznego . W kompasie magnetycznym biegun północny magnesu sztabkowego wskazuje północ. Oznacza to jednak, że geomagnetyczny biegun północny Ziemi jest południowym (biegunem poszukującym południa) jego momentu dipolowego i odwrotnie.

Jedynymi znanymi mechanizmami tworzenia dipoli magnetycznych są pętle prądowe lub spin kwantowo-mechaniczny, ponieważ nigdy nie wykazano eksperymentalnie istnienia monopoli magnetycznych .

Klasyfikacja

Linie pola elektrycznego dwóch przeciwstawnych ładunków oddzielonych skończoną odległością.

Linie pola magnetycznego prądu pierścieniowego o skończonej średnicy.

Linie pola dipola punktowego dowolnego typu, elektrycznego, magnetycznego, akustycznego itp.

Fizyczny dipol składa się z dwóch równych i przeciwnych ładunków punktowych: w dosłownym znaczeniu dwóch biegunów. Jego pole przy dużych odległościach (tj. odległościach dużych w porównaniu z odległością od siebie biegunów) zależy prawie całkowicie od momentu dipolowego, jak zdefiniowano powyżej. punktowy (elektryczny) to granica uzyskana przez pozwolenie separacji na dążenie do 0 przy jednoczesnym utrzymaniu stałego momentu dipolowego. Pole dipola punktowego ma szczególnie prostą postać, a człon rzędu 1 w rozwinięciu multipolowym jest właśnie polem dipolowym.

Chociaż w przyrodzie nie ma znanych monopoli magnetycznych , istnieją dipole magnetyczne w postaci spinu kwantowo-mechanicznego związanego z cząstkami takimi jak elektrony (chociaż dokładny opis takich efektów wykracza poza klasyczny elektromagnetyzm). Teoretyczny punktowy dipol magnetyczny ma pole magnetyczne o dokładnie takiej samej postaci jak pole elektryczne punktu elektrycznego. Bardzo mała pętla przewodząca prąd jest w przybliżeniu dipolem punktu magnetycznego; magnetyczny moment dipolowy takiej pętli jest iloczynem prądu płynącego w pętli i pola (wektorowego) pętli.

Każda konfiguracja ładunków lub prądów ma „moment dipolowy”, który opisuje dipol, którego pole jest najlepszym przybliżeniem, na dużych odległościach, pola danej konfiguracji. Jest to po prostu jeden składnik w rozwinięciu wielobiegunowym, gdy całkowity ładunek („moment monopolowy”) wynosi 0 - jak to zawsze ma miejsce w przypadku magnetycznego, ponieważ nie ma monopoli magnetycznych. Składnik dipolowy jest dominujący na dużych odległościach: jego pole spada proporcjonalnie do 1 / r ³ , w porównaniu do 1 / r ⁴ dla następnego ( kwadrupolowego ) składnika i wyższych potęg 1 / r dla wyższych składników, czyli 1 / r ² dla terminu monopolu.

Dipole molekularne

Zobacz też: Polarność chemiczna

Wiele cząsteczek ma takie momenty dipolowe z powodu nierównomiernego rozkładu ładunków dodatnich i ujemnych na różnych atomach. Tak jest w przypadku związków polarnych, takich jak fluorowodór (HF), w których gęstość elektronów rozkłada się nierównomiernie między atomami. Dlatego dipol cząsteczki jest dipolem elektrycznym z własnym polem elektrycznym, którego nie należy mylić z dipolem magnetycznym , który generuje pole magnetyczne.

Fizykochemik Peter JW Debye był pierwszym naukowcem, który dogłębnie zbadał dipole molekularne, w związku z czym momenty dipolowe są mierzone w jednostce spoza układu SI , nazwanej na jego cześć debye .

W przypadku cząsteczek istnieją trzy rodzaje dipoli:

Dipole trwałe

Występują, gdy dwa atomy w cząsteczce mają zasadniczo różną elektroujemność : jeden atom przyciąga elektrony bardziej niż inny, stając się bardziej ujemny, podczas gdy drugi atom staje się bardziej dodatni. Cząsteczka o stałym momencie dipolowym nazywana jest polarną . Zobacz atrakcje dipol-dipol .

Chwilowe dipole

Występują przypadkowo, gdy elektrony są bardziej skoncentrowane w jednym miejscu niż w innym w cząsteczce , tworząc tymczasowy dipol. Dipole te mają mniejszą wielkość niż dipole trwałe, ale nadal odgrywają dużą rolę w chemii i biochemii ze względu na ich rozpowszechnienie. Zobacz chwilowy dipol .

Dipole indukowane

Mogą one wystąpić, gdy jedna cząsteczka ze stałym dipolem odpycha elektrony innej cząsteczki, indukując moment dipolowy w tej cząsteczce. Cząsteczka jest spolaryzowana , gdy zawiera indukowany dipol. Zobacz przyciąganie dipolowe indukowane .

Mówiąc bardziej ogólnie, indukowany dipol o dowolnym polaryzowalnym rozkładzie ładunku ρ (pamiętaj, że cząsteczka ma rozkład ładunku) jest powodowany przez pole elektryczne zewnętrzne względem ρ . Pole to może na przykład pochodzić od jonu lub cząsteczki polarnej w pobliżu ρ lub może być makroskopowe (np. cząsteczka między okładkami naładowanego kondensatora ) . Wielkość indukowanego momentu dipolowego jest równa iloczynowi natężenia pola zewnętrznego i polaryzowalności dipolowej ρ .

Wartości momentu dipolowego można uzyskać z pomiaru stałej dielektrycznej . Niektóre typowe wartości fazy gazowej w jednostkach debye to:

• dwutlenek węgla : 0
• tlenek węgla : 0,112 D
• ozon : 0,53 D
• fosgen : 1,17 D
• NH ₃ ma moment dipolowy 1,42 D
• para wodna : 1,85 D
• cyjanowodór : 2,98 D
• cyjanamid : 4,27 D
• bromek potasu : 10,41 D

Liniowa cząsteczka CO ₂ ma zerowy dipol, ponieważ dwa dipole wiążące znoszą się.

Bromek potasu (KBr) ma jeden z najwyższych momentów dipolowych, ponieważ jest związkiem jonowym występującym jako cząsteczka w fazie gazowej.

Wygięta cząsteczka H ₂ O ma dipol netto. Dwa dipole wiązań nie anulują się.

Całkowity moment dipolowy cząsteczki można przybliżyć jako sumę wektorową momentów dipolowych wiązań . Jako suma wektorów zależy to od względnej orientacji wiązań, tak że z momentu dipolowego można wywnioskować informacje o geometrii cząsteczki .

Na przykład dipol zerowy CO ₂ implikuje, że dwa momenty dipolowe wiązania C=O znoszą się, więc cząsteczka musi być liniowa. Dla H ₂ O momenty wiązań O−H nie znoszą się, ponieważ cząsteczka jest wygięta. Dla ozonu (O ₃ ), który jest również zakrzywioną cząsteczką, momenty dipolowe wiązań nie są zerowe, mimo że wiązania O-O występują między podobnymi atomami. Jest to zgodne ze strukturami Lewisa dla form rezonansowych ozonu, które wykazują ładunek dodatni na centralnym atomie tlenu.

cis , moment dipolowy 1,90 D

trans , moment dipolowy zero

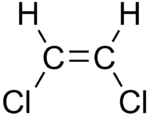
Przykładem w chemii organicznej roli geometrii w określaniu momentu dipolowego są izomery cis i trans 1,2- dichloroetenu . W cis dwa polarne wiązania C-Cl znajdują się po tej samej stronie podwójnego wiązania C=C, a cząsteczkowy moment dipolowy wynosi 1,90 D. W izomerze trans moment dipolowy wynosi zero, ponieważ dwa wiązania C-Cl są po przeciwnych stronach C=C i anulują się (a dwa momenty wiązań dla znacznie mniej polarnych wiązań C-H również się anulują).

Innym przykładem roli geometrii molekularnej jest trifluorek boru , który ma trzy wiązania polarne z różnicą elektroujemności większą niż tradycyjnie podawany próg 1,7 dla wiązania jonowego . Jednak ze względu na równoboczny trójkątny rozkład jonów fluorkowych wyśrodkowanych na tej samej płaszczyźnie co kation boru iw tej samej płaszczyźnie co kation boru, symetria cząsteczki powoduje, że jej moment dipolowy wynosi zero.

Kwantowy mechaniczny operator dipolowy

Rozważmy zbiór N cząstek o ładunkach q _i i wektorach położenia r _i . Na przykład tym zbiorem może być cząsteczka składająca się z elektronów, z których wszystkie mają ładunek − e , oraz jąder o ładunku eZ _i , gdzie Z _i jest liczbą atomową i - tego jądra. Obserwowalny dipol (wielkość fizyczna) ma kwantowo-mechaniczny operator dipolowy :

${\ Displaystyle {\ mathfrak {p}} = \ suma _ {i = 1} ^ {N} \, q_ {i} \, \ mathbf {r} _ {i} \,.}$

Zauważ, że ta definicja obowiązuje tylko dla neutralnych atomów lub cząsteczek, tzn. całkowity ładunek równy zeru. W zjonizowanym przypadku mamy

${\ Displaystyle {\ mathfrak {p}} = \ suma _ {i = 1} ^ {N} \, q_ {i} \, (\ mathbf {r} _ {i}-\mathbf {r} _ {c}),}$

gdzie $\ mathbf {r} _ {c}} .$ środkiem masy cząsteczki / grupy cząstek r do {\

Dipole atomowe

niezdegenerowany ( stan S ) może mieć tylko zerowy trwały dipol. Fakt ten wynika z kwantowo-mechanicznej symetrii atomów. Wszystkie 3 składowe operatora dipolowego są antysymetryczne przy inwersji względem jądra,

${\ Displaystyle {\ mathfrak {I}} \; {\ mathfrak {p}} \; {\ mathfrak {I}} ^ {- 1} = - {\ mathfrak {p} },}$

gdzie $inwersji$ operatorem dipolowym i $jest$ .

Stały moment dipolowy atomu w stanie niezdegenerowanym (patrz zdegenerowany poziom energii ) jest podawany jako oczekiwana (średnia) wartość operatora dipolowego,

${\ Displaystyle \ lewo \ langle {\ mathfrak {p}} \ prawo \ rangle = \ lewo \ langle \, S \, | {\ mathfrak {p}} | \, S \, \ prawo \ rangle, }$

gdzie ${\ Displaystyle |\, S \, \ rangle}$ jest funkcją falową w stanie S , niezdegenerowaną, która jest symetryczna lub antysymetryczna przy odwróceniu: ${\ Displaystyle {\ mathfrak {I}} \,|\, S \, \ rangle = \ pm |\, S \, \ rangle}$ . Ponieważ iloczyn funkcji falowej (w ket) i jej złożonego koniugatu (w staniku) jest zawsze symetryczny pod wpływem inwersji i jej odwrotności,

${\ Displaystyle \ lewo \ langle {\ mathfrak {p}} \ prawo \ rangle = \ lewo \ langle \, {\ mathfrak {I}} ^ {- 1} \, S \, | {\mathfrak {p}}|\,{\mathfrak {I}}^{-1}\,S\,\right\rangle =\left\langle \,S\,|{\mathfrak {I}}\ ,{\mathfrak {p}}\,{\mathfrak {I}}^{-1}|\,S\,\right\rangle =-\left\langle {\mathfrak {p}}\right\rangle}$

wynika z tego, że wartość oczekiwana zmienia znak pod wpływem inwersji. Wykorzystaliśmy tutaj fakt, że będąc operatorem symetrii, jest $- 1} = { \ mathfrak {I}} ^ {*} \,}$ - 1 ${$ iz definicji sprzężenie hermitowskie ${\ Displaystyle {\ mathfrak {I}} ^ {*} \,}$ może zostać przeniesione z biustonosza do ket, a następnie staje się ${\ Displaystyle {\ mathfrak {I}} ^ {**} = {\ mathfrak {I}} \,}$ . Ponieważ jedyną wielkością równą samemu minusowi jest zero, wartość oczekiwana znika,

${\ Displaystyle \ lewo \ langle {\ mathfrak {p}} \ prawo \ rangle = 0.}$

W przypadku atomów z otwartą powłoką o zdegenerowanych poziomach energii moment dipolowy można określić za pomocą efektu Starka pierwszego rzędu . Daje to niezanikający dipol (z definicji proporcjonalny do niezanikającego przesunięcia Starka pierwszego rzędu) tylko wtedy, gdy niektóre funkcje falowe należące do zdegenerowanych energii mają przeciwną parzystość ; tj. mają różne zachowanie w przypadku inwersji. Jest to rzadkie zjawisko, ale zdarza się w przypadku wzbudzonego atomu H, w którym stany 2s i 2p są „przypadkowo” zdegenerowane (patrz artykuł Laplace – Runge – Lenz wektor o pochodzeniu tej degeneracji) i mają przeciwną parzystość (2s jest parzysta i 2p jest nieparzyste).

Pole statycznego dipola magnetycznego

Zobacz też: Magnes § Dwa modele magnesów: bieguny magnetyczne i prądy atomowe

Ogrom

Natężenie pola dalekiego B dipolowego pola magnetycznego jest określone wzorem

${\ Displaystyle B (m, r, \ lambda) = {\ Frac {\ mu _ {0}} { 4\pi }}{\frac {m}{r^{3}}}{\sqrt {1+3\sin ^{2}(\lambda )}}\,,}$

Gdzie

B to natężenie pola mierzone w teslach

r to odległość od centrum mierzona w metrach

λ to szerokość geograficzna magnetyczna (równa 90° − θ ) gdzie θ to colatitude magnetyczna mierzona w radianach lub stopniach od dipola oś

m to moment dipolowy mierzony w ampero -metrach kwadratowych lub dżulach na teslę

₀ μ to przepuszczalność wolnej przestrzeni mierzona w henrach na metr.

Konwersję na współrzędne cylindryczne uzyskuje się za pomocą r ² = z ² + ρ ² i

${\ Displaystyle \ lambda = \ arcsin \ lewo ({\ Frac {z} {\ sqrt {z ^ {2} + \ rho ^ {2}}}} \ prawo )}$

gdzie ρ jest prostopadłą odległością od osi z . Następnie,

${\ Displaystyle B (\ rho, z) = {\ Frac {\ mu _ {0 }m}{4\pi \left(z^{2}+\rho ^{2}\right)^{\frac {3}{2}}}}{\sqrt {1+{\frac {3z^ {2}}{z^{2}+\rho^{2}}}}}}$

Forma wektorowa

Samo pole jest wielkością wektorową:

${\ Displaystyle \ mathbf {B} (\ mathbf {m}, \ mathbf {r}) = {\ Frac {\ mu _{0}}{4\pi}}\ {\frac {3(\mathbf {m} \cdot {\kapelusz {\mathbf {r}}}){\kapelusz {\mathbf {r}}}- \mathbf {m} }{r^{3}}}}$

Gdzie

B to pole

r to wektor od pozycji dipola do pozycji, w której mierzone jest pole

r to wartość bezwzględna r : odległość od dipola

r̂ = r / r to wektor jednostkowy równoległy do ​​r ;

m to (wektorowy) moment dipolowy

₀ μ to przepuszczalność wolnej przestrzeni

Jest to dokładnie pole dipola punktowego, dokładnie człon dipolowy w wielobiegunowym rozwinięciu dowolnego pola iw przybliżeniu pole dowolnej konfiguracji podobnej do dipoli na duże odległości.

Magnetyczny potencjał wektorowy

Potencjał wektorowy A dipola magnetycznego wynosi

${\ Displaystyle \ mathbf {A} (\ mathbf {r}) = {\ Frac {\ mu _ {0}} {4 \ pi}} {\ Frac {\mathbf {m} \times {\ kapelusz {\mathbf {r}}}}{r^{2}}}}$

z tymi samymi definicjami, co powyżej.

Pole z dipola elektrycznego

Potencjał elektrostatyczny w pozycji r wywołany dipolem elektrycznym na początku jest określony wzorem:

${\ Displaystyle \ Phi (\ mathbf {r}) = {\ Frac {1} {4 \ pi \ epsilon _ {0}}} \, {\ frac {\mathbf {p} \cdot {\ kapelusz {\mathbf {r}}}}{r^{2}}}}$

₀ gdzie p jest (wektorowym) momentem dipolowym , a є jest przenikalnością wolnej przestrzeni .

Składnik ten pojawia się jako drugi składnik w wielobiegunowym rozwinięciu dowolnego potencjału elektrostatycznego Φ( r ). Jeśli źródłem Φ( r ) jest dipol, jak tu założono, to człon ten jest jedynym niezerującym wyrazem w rozwinięciu multipolowym Φ( r ). Pole elektryczne z dipola można znaleźć z gradientu tego potencjału:

${\ Displaystyle \ mathbf {E} = - \ nabla \ Phi = {\ Frac {1} {4 \ pi \ epsilon _ {0}}} \ {\ Frac {3 (\ mathbf {p} \ cdot {\ kapelusz {\mathbf {r}}}){\hat {\mathbf {r}}}-\mathbf {p} }{r^{3}}}-\delta ^{3}(\mathbf {r}){ \frac {\mathbf {p}}{3\epsilon_{0}}}.}$

Jest to ta sama forma wyrażenia dla pola magnetycznego punktowego dipola magnetycznego, pomijając funkcję delta. Jednak w prawdziwym dipolu elektrycznym ładunki są fizycznie oddzielone, a pole elektryczne rozchodzi się lub zbiega w punktach ładunków. Różni się to od pola magnetycznego prawdziwego dipola magnetycznego, które jest wszędzie ciągłe. Funkcja delta reprezentuje silne pole skierowane w przeciwnym kierunku między ładunkami punktowymi, co często jest pomijane, ponieważ rzadko interesuje nas pole w pozycji dipola. Dalsze dyskusje na temat wewnętrznego pola dipoli można znaleźć w artykule Moment magnetyczny # Wewnętrzne pole magnetyczne dipola .

Moment obrotowy na dipolu

Ponieważ kierunek pola elektrycznego jest zdefiniowany jako kierunek siły działającej na ładunek dodatni, linie pola elektrycznego skierowane są od ładunku dodatniego w kierunku ładunku ujemnego.

Po umieszczeniu w jednorodnym polu elektrycznym lub magnetycznym po obu stronach dipola powstają równe, ale przeciwne siły , tworzące moment obrotowy τ }:

${\ Displaystyle {\ boldsymbol {\ tau}} = \ mathbf {p} \ razy \ mathbf {E}}$

dla elektrycznego momentu dipolowego p (w kulombometrach) lub

${\ Displaystyle {\ boldsymbol {\ tau}} = \ mathbf {m} \ razy \ mathbf {B}}$

dla magnetycznego momentu dipolowego m (w amperach kwadratowych).

Wynikowy moment obrotowy będzie dążył do wyrównania dipola z przyłożonym polem, co w przypadku dipola elektrycznego daje energię potencjalną

${\ Displaystyle U = - \ mathbf {p} \ cdot \ mathbf {E}}$ .

Energia dipola magnetycznego jest podobna

${\ Displaystyle U = - \ mathbf {m} \ cdot \ mathbf {B}}$ .

Promieniowanie dipolowe

Moduł wektora Poyntinga dla oscylującego dipola elektrycznego (rozwiązanie dokładne). Te dwa ładunki są pokazane jako dwie małe czarne kropki.

Zobacz też: Antena dipolowa

Oprócz dipoli w elektrostatyce często bierze się również pod uwagę dipol elektryczny lub magnetyczny, który oscyluje w czasie. Jest to rozszerzenie lub bardziej fizyczny następny krok do falowego .

₀ W szczególności rozważ harmonicznie oscylujący dipol elektryczny o częstotliwości kątowej ω i momencie dipolowym p wzdłuż kierunku ẑ postaci

${\ Displaystyle \ mathbf {p} (\ mathbf {r}, t) = \ mathbf {p} (\ mathbf {r}) e ^ {-i \ omega t} = p_ {0} {\ kapelusz {\ mathbf {z} }}e^{-i\omega t}.}$

W próżni dokładne pole wytwarzane przez ten oscylujący dipol można wyprowadzić za pomocą wzoru na potencjał opóźniony jako:

${\ Displaystyle {\ rozpocząć {wyrównane} \ mathbf {E} & = {\ Frac {1} {4 \ pi \ varepsilon _ {0}}} \ lewo \ {{\ Frac {\ omega ^ {2}}} c^{2}r}}\left({\hat {\mathbf {r}}}\times \mathbf {p} \right)\times {\hat {\mathbf {r}}}+\left({ \frac {1}{r^{3}}}-{\frac {i\omega }{cr^{2}}}\right)\left(3{\hat {\mathbf {r}}}\left [{\hat {\mathbf {r}}}\cdot \mathbf {p} \right]-\mathbf {p} \right)\right\}e^{\frac {i\omega r}{c}} e^{-i\omega t}\\\mathbf {B} &={\frac {\omega ^{2}}{4\pi \varepsilon _{0}c^{3}}}({\hat {\mathbf {r}}}\times \mathbf {p} )\left(1- {\frac {c}{i\omega r}}\right){\frac {e^{i\omega r/c }}{r}}e^{-i\omega t}.\end{wyrównane}}}$

Dla rω / c ≫ 1 pole dalekie przybiera prostszą postać promieniującej fali „sferycznej”, ale z zależnością kątową osadzoną w iloczynie krzyżowym:

${\ Displaystyle {\ rozpocząć {wyrównane} \ mathbf {B} & = {\ Frac {\ omega ^ {2}} {4 \ pi \ varepsilon _ {0} c ^ {3}}} ({\ kapelusz {\ mathbf {r}}}\times \mathbf {p} ){\frac {e^{i\omega (r/ct)}}{r}}={\frac {\omega ^{2}\mu _{ 0}p_{0}}{4\pi c}}({\kapelusz {\mathbf {r}}}\razy {\kapelusz {\mathbf {z}}}){\frac {e^{i\omega (r/ct)}}{r}}=-{\frac {\omega ^{2}\mu _{0}p_{0}}{4\pi c}}\sin(\theta){\frac {e^{i\omega (r/ct)}}{r}}\mathbf {\hat {\phi}} \\\mathbf {E} &=c\mathbf {B} \times {\hat {\ mathbf {r}}}=-{\frac {\omega ^{2}\mu _{0}p_{0}}{4\pi}}\sin(\theta)\left({\kapelusz {\fi }}\times \mathbf {\hat {r}} \right){\frac {e^{i\omega (r/ct)}}{r}}=-{\frac {\omega ^{2}\ mu _{0}p_{0}}{4\pi}}\sin(\theta){\frac {e^{i\omega (r/ct)}}{r}}{\kapelusz {\theta} }.\end{wyrównane}}}$

Uśredniony w czasie wektor Poyntinga

${\ Displaystyle \ langle \ mathbf {S} \ rangle = \ lewo ({\ Frac {\ mu _ {0 }p_{0}^{2}\omega ^{4}}{32\pi ^{2}c}}\right){\frac {\sin ^{2}(\theta)}{r^{2 }}}\mathbf {\kapelusz {r}}}$

nie jest rozłożony izotropowo, ale skoncentrowany wokół kierunków leżących prostopadle do momentu dipolowego, w wyniku niesferycznych fal elektrycznych i magnetycznych. W rzeczywistości sferyczna funkcja harmoniczna (sin θ ) odpowiedzialna za taki toroidalny rozkład kątowy to właśnie fala l = 1 „p”.

Całkowitą średnią w czasie moc wypromieniowaną przez pole można następnie wyprowadzić z wektora Poyntinga jako

${\ Displaystyle P = {\ Frac {\ mu _ {0} \ omega ^ {4} p_ {0} ^ {2}} {12 \ pi c}}.}$

Zauważ, że zależność mocy od czwartej potęgi częstotliwości promieniowania jest zgodna z rozpraszaniem Rayleigha i leżącymi u jego podstaw efektami, dlaczego niebo składa się głównie z koloru niebieskiego.

Dipol spolaryzowany kołowo jest opisywany jako superpozycja dwóch dipoli liniowych.

Zobacz też

• Gęstość polaryzacji
• Modele dipoli magnetycznych
• Model dipolowy pola magnetycznego Ziemi
• Elektret
• Dipol Oceanu Indyjskiego i Subtropikalny Dipol Oceanu Indyjskiego , dwa zjawiska oceanograficzne
• Magnetyczne oddziaływanie dipol-dipol
• Spinowy moment magnetyczny
• Monopol
• Solidne harmoniczne
• Osiowe momenty wielobiegunowe
• Cylindryczne momenty wielobiegunowe
• Sferyczne momenty wielobiegunowe
• Rozwinięcie Laplace'a
• Ciało stałe molekularne
• Moment magnetyczny # Wewnętrzne pole magnetyczne dipola

Linki zewnętrzne

• Program geomagnetyzmu USGS
• Fields of Force : rozdział z internetowego podręcznika
• Elektryczny potencjał dipolowy autorstwa Stephena Wolframa i gęstość energii dipola magnetycznego autorstwa Franza Kraffta. Projekt Demonstracje Wolframa .