Równoważny promień anteny

Równoważny promień przewodu antenowego definiuje się jako:

${\ Displaystyle r_ {e} = \ exp \ lewo \ {{1 \ nad L ^ {2}} \ oint _ {\ ell} \ oint _ {\ ell} \ ln \ vert {\ pogrubiony symbol {x}}-{\boldsymbol {y}}\vert \;dx\;dy\right\}}$

gdzie ${\ Displaystyle \ scriptstyle \ ell} oznacza$ obwód przewodnika , ${\ Displaystyle \ scriptstyle {L}}$$\ scriptstyle {\ boldsymbol {y}}}$ długość obwodu, i $\ scriptstyle {\ boldsymbol {x}}}$$displaystyle$$displaystyle$ to wektory lokalizujące punkty wzdłuż obwodu, a i $to$ segmenty różniczkowe Promień równoważny pozwala na wykorzystanie wzorów analitycznych lub danych obliczeniowych lub eksperymentalnych uzyskanych dla anten zbudowanych z małych przewodników o jednorodnych, okrągłych przekrojach poprzecznych do zastosowania w analizie anten zbudowanych z małych przewodników o jednorodnych, niekołowych przekrojach poprzecznych. Tutaj „mały” oznacza $, że$ ​​największy wymiar przekroju poprzecznego jest znacznie mniejszy niż długość .

Formuły

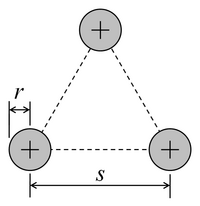
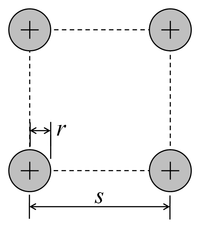
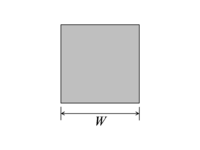
W poniższej tabeli wymieniono równoważne promienie dla różnych przekrojów przewodów wyprowadzone przy założeniu, że 1) wszystkie wymiary są znacznie mniejsze niż , 2) dla przekrojów składających się z wielu przewodów odległości między przewodami wynoszą ${\ displaystyle \ scriptstyle {\ lambda}}$ znacznie większy niż jakikolwiek wymiar pojedynczego przewodnika. . Wzory na przekrój kwadratowy i trójkątny wynikają z numerycznego obliczenia całki podwójnej. Wszystkie inne formuły są dokładne.

Przekrój	Opis	Równoważny promień
	Dwa identyczne okrągłe przewodniki	${\ Displaystyle {\ sqrt {rs}}}$
	Dwa okrągłe przewodniki o nierównych promieniach	${\ Displaystyle \ exp \ lewo \ {{r_ {1} ^{2}\ln r_{1}+r_{2}^{2}\ln r_{2}+2r_{1}r_{2}\ln S \over (r_{1}+r_{2}) ^{2}}\prawo\}}$
	Identyczne okrągłe przewodniki ułożone w trójkąt	${\ Displaystyle \ lewo (rs ^ {2} \ prawo) ^ {1/3}}$
	Identyczne okrągłe przewodniki ułożone w kwadracie	${\ Displaystyle \ lewo ({\ sqrt {2}} \ rs ^ {3} \ prawej) ^ {1/4}}$
	Identyczne okrągłe przewodniki ułożone w pięciokąt	${\ Displaystyle \ lewo (2,62 \, rs ^ {4} \ prawo) ^ {1/5}}$
	Identyczne okrągłe przewodniki ułożone w sześciokąt	${\ Displaystyle \ lewo (6 \, rs ^ {5} \ prawo) ^ {1/6}}$
	${\ displaystyle N}$ Identyczne okrągłe przewodniki równomiernie rozmieszczone wokół okręgu	${\ Displaystyle \ lewo (NrR ^ {N-1} \ prawo) ^ {1/N}}$
	Płaski, nieskończenie cienki przewodnik	${-3/2} \ około 0,22 \, W}}$
	Kwadratowy dyrygent	${\ Displaystyle \ Displaystyle {0,58 \, W}}$
	Przewodnik trójkąta równobocznego	${\ Displaystyle \ Displaystyle {0,41 \, W}}$

Pochodzenie

Równoważny promień uzyskuje się przez zrównanie średniego potencjału wektora magnetycznego na powierzchni przewodnika o dowolnym przekroju z potencjałem na powierzchni walca.

Załóżmy, że wymiary przekroju poprzecznego przewodnika są małe w porównaniu z długością fali, prąd płynie tylko osiowo wzdłuż przewodnika, rozkład prądu powoli zmienia się wzdłuż długości przewodnika, a prąd jest w przybliżeniu równomiernie rozłożony wzdłuż jego obwodu (ze względu na efekt naskórkowy ) . Co więcej, tylko prąd w sąsiedztwie dowolnego punktu przewodnika znacząco wpływa na potencjał w tym punkcie. Zależność od czasu jest ignorowana, ponieważ można ją uwzględnić, mnożąc rozkład prądu przez zmienną w czasie sinusoidę. $)$ i że geometria jest w rzeczywistości jedną z nieskończenie długich przewodników o stałej gęstości prądu powierzchniowego (prąd na powierzchnię , zmniejszając w ten sposób trzy problemu dwuwymiarowego na problem dwuwymiarowy. Sugeruje się również, że potencjał wektora magnetycznego jest równoległy do ​​osi przewodnika.

Najpierw rozważ potencjał w stałym punkcie $.$ obwodzie dowolnego przekroju Gdy obwód jest podzielony na segmenty różnicowe , rozkład prądu można przybliżyć, umieszczając prąd w linii pionowej w każdym segmencie, z których każdy ma gęstość liniową $re$$\ scriptstyle { Q\,dx}}$ (prąd na długość). Powszechnie wiadomo, że potencjał takiego prądu liniowego wynosi ${\ Displaystyle \ scriptstyle {- (\ mu _ {0} Qdx / 2 \ pi) \ ln \ vert {\ boldsymbol {x}} - {\ boldsymbol {y}} \ vert}}, gdzie μ {$ \ $\ scriptstyle {\mu _{0}}}$ to stała przepuszczalności. Potencjał w jest sumą potencjałów dla wszystkich pasków, czyli ${\ displaystyle \ scriptstyle {\ boldsymbol {y}}}$

${\ Displaystyle A ({\ boldsymbol {y}}) = - {\ mu _ {0} Q \ ponad 2 \ pi} \ oint _ {\ ell} \ ln \ vert {\ boldsymbol {x}} - {\ symbol pogrubienia {y}}\vert \;dx.}$

Średni potencjał jest wtedy

${\ Displaystyle {\ bar {A}} = {1 \ ponad L} \ oint _ {\ ell} A ({\ boldsymbol {y}}) \; dy \, = - {\ mu _ {0} Q \ nad 2\pi L}\oint _{\ell }\oint _{\ell }\ln \vert {\boldsymbol {x}}-{\boldsymbol {y}}\vert \;dx\;dy.}$

Rozważmy teraz przypadek cylindra o takiej samej liniowej gęstości prądu jak przewodnik o dowolnym przekroju. Wiadomo również, że potencjał w dowolnym punkcie na jego powierzchni, który jest również równy jego średniemu potencjałowi, wynosi

${\ Displaystyle A_ {c} = - {\ mu _ {0} QL \ ponad 2 \ pi} \ ln \ lewo (r_ {e} \ prawo).}$

Zrównanie daje ${\ Displaystyle \ scriptstyle {\ bar {A}}}$ i ${\ Displaystyle \ scriptstyle {A_ {c}}}$

${\ Displaystyle \ ln \ lewo (r_ {e} \ prawo) = {1 \ nad L ^ {2}} \ oint _ {\ ell} \ oint _ {\ ell} \ ln \ vert {\ boldsymbol {x} }-{\boldsymbol {y}}\vert \;dx\;dy.}$

Potęgowanie obu stron prowadzi do wzoru na równoważny promień.

Wzór na równoważny promień zapewnia spójne wyniki. Jeśli wymiary przekroju poprzecznego przewodu są skalowane przez współczynnik $,$ promień jest skalowany przez ${\ Displaystyle \ scriptstyle {|\ alfa |}}$ . Również równoważny promień cylindrycznego przewodnika jest równy promieniowi przewodnika.