Rozszczepienie bieguna

Rozszczepianie biegunów jest zjawiskiem wykorzystywanym w niektórych formach kompensacji częstotliwości stosowanych we wzmacniaczach elektronicznych . Kiedy kondensator jest wprowadzony między stronę wejściową i wyjściową wzmacniacza z zamiarem przesunięcia bieguna o najniższej częstotliwości (zwykle bieguna wejściowego) do niższych częstotliwości, rozszczepienie biegunów powoduje ruch bieguna o następnej częstotliwości (zwykle biegun wyjściowy). na wyższą częstotliwość. Ten ruch biegunów zwiększa stabilność wzmacniacza i poprawia jego odpowiedź skokową kosztem zmniejszonej prędkości.

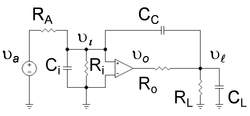
Przykład podziału biegunów

Rysunek 1: Wzmacniacz operacyjny z kondensatorem kompensacyjnym C _C między wejściem a wyjściem; zauważ, że wzmacniacz ma zarówno impedancję wejściową R _i jak i impedancję wyjściową R _o .

Rysunek 2: Wzmacniacz operacyjny z kondensatorem kompensacyjnym przekształconym przy użyciu twierdzenia Millera w celu zastąpienia kondensatora kompensacyjnego kondensatorem Millera na wejściu i zależnym od częstotliwości źródłem prądu na wyjściu.

Ten przykład pokazuje, że wprowadzenie kondensatora oznaczonego jako C _C we wzmacniaczu z rysunku 1 ma dwa skutki: po pierwsze powoduje, że biegun najniższej częstotliwości wzmacniacza przesuwa się jeszcze niżej, a po drugie, powoduje, że biegun wyższy przesuwa się wyżej w częstotliwości. Wzmacniacz z rysunku 1 ma biegun niskiej częstotliwości , _ze względu na dodatkową rezystancję wejściową _Ri RA || _Ri i _pojemność Ci ze stałą czasową Ci _. ( ) Częstotliwość tego bieguna jest obniżana przez efekt Millera . Wzmacniacz otrzymuje biegun wyjściowy wysokiej częstotliwości przez dodanie rezystancji obciążenia R _L i pojemności C _L , ze stałą czasową C _L ( R _o || R _L ). Ruch w górę bieguna wysokiej częstotliwości występuje, ponieważ wzmacniany przez Millera kondensator kompensacyjny C _C zmienia zależność częstotliwościową dzielnika napięcia wyjściowego.

Pierwszy cel, aby pokazać, że najniższy biegun maleje z częstotliwością, jest ustalany przy użyciu tego samego podejścia, co artykuł z twierdzenia Millera . Postępując zgodnie z procedurą opisaną w artykule na temat twierdzenia Millera , obwód z rysunku 1 przekształca się w obwód z rysunku 2, który jest elektrycznie równoważny z rysunkiem 1. Zastosowanie prawa Kirchhoffa do strony wejściowej rysunku 2 określa napięcie wejściowe ${\ displaystyle \ v_ {i}}$ do idealnego wzmacniacza operacyjnego w funkcji przyłożonego napięcia sygnału ${\ Displaystyle \ v_ {a}}$ , a mianowicie

${\ Displaystyle {\ Frac {v_ {i}} {v_ {a}} }={\frac {R_{i}}{R_{i}+R_{A}}}{\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A }\|R_{i})}}\ ,}$

który wykazuje spadek z częstotliwością zaczynającą się od f ₁ gdzie

${\ Displaystyle {\ rozpocząć {wyrównane} f_ {1} i = {\ Frac {1} {2} \pi (C_{M}+C_{i})(R_{A}\|R_{i})}}\\&={\frac {1}{2\pi \tau _{1}}}\ ,\\\koniec {wyrównany}}}$

$co$ wprowadza notację najniższego bieguna. Ta częstotliwość { _jest niższa niż początkowa niska częstotliwość wzmacniacza, która dla $\ pi C_ {i$ \ .

Przechodząc do drugiego celu, pokazującego, że wyższy biegun porusza się z jeszcze większą częstotliwością, konieczne jest spojrzenie na wyjściową stronę obwodu, która ma drugi czynnik w ogólnym wzmocnieniu i dodatkową zależność częstotliwości. Napięcie $\ displaystyle \ v_ {o}}$ określane przez wzmocnienie idealnego wzmacniacza operacyjnego wewnątrz wzmacniacza jako v o

${\ Displaystyle \ v_ {o} = A_ {v} v_ {i} \ .}$

Korzystając z tej zależności i stosując obecne prawo Kirchhoffa do wyjściowej strony obwodu, określa się napięcie obciążenia jako funkcję napięcia na wejściu $\ ell}$$\ displaystyle v _ {$ do idealnego wzmacniacza operacyjnego jako:

${o}}}\,\!}$${\ Displaystyle {\ Frac {v_ {\ ell}} {v_ {i}}} = A_ {v} {\ Frac {R_ {L}} {R_ {L}+$${\ Displaystyle \ cdot {\ Frac {1 + j \ omega C_ {C} R_ {o} / A_ {v}} {1 + j \ omega (C_ {L} + C_ {C}) (R_ {o} \|R_{L})}}\ .}$

To wyrażenie jest łączone ze współczynnikiem wzmocnienia znalezionym wcześniej dla strony wejściowej obwodu, aby uzyskać całkowite wzmocnienie jako

${\ Displaystyle {\ Frac {v_ {\ ell}} {v_ {a}}} = {\ Frac {v_ {\ ell}} {v_ {i}} {\ Frac {v_ {i}} {v_ {a}}}}$

${\ Displaystyle = A_ {v} {\ Frac {R_ { i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\,\!}$${\ Displaystyle \ cdot {\ Frac {1} {1 + j \ omega (C_ {M} + C_ {i}) (R_ {A} \| R_$${\ Displaystyle \ cdot {\ Frac {1 + j \ omega C_ {C} R_ {o} / A_ {v}} {1 + j \ omega (C_ {L} + C_ {C}) (R_ {o} \|R_{L})}}\ .}$

Ten wzór wzmocnienia wydaje się pokazywać prostą odpowiedź dwubiegunową z dwiema stałymi czasowymi. (Wykazuje również zero w liczniku, ale zakładając, że wzmocnienie wzmacniacza Av jest duże, to zero jest ważne tylko przy częstotliwościach zbyt wysokich, aby mieć znaczenie _w tej dyskusji, więc licznik można przybliżyć jako jedność.) Jednakże, chociaż wzmacniacz ma zachowanie dwubiegunowe, dwie stałe czasowe są bardziej skomplikowane, niż sugeruje powyższe wyrażenie, ponieważ pojemność Millera zawiera ukrytą zależność częstotliwościową, która nie ma znaczenia przy niskich częstotliwościach, ale ma znaczący wpływ na wysokie częstotliwości. To znaczy, zakładając wyjście RC iloczyn CL _{przybliżenia} ( R _o || R _L ) odpowiada częstotliwości znacznie powyżej bieguna niskiej częstotliwości, należy użyć dokładnej postaci pojemności Millera, a nie Millera . Zgodnie z artykułem na temat efektu Millera , pojemność Millera jest dana przez

${\ Displaystyle {\ rozpocząć {wyrównane} C_ {M} & = C_ {C} \ lewo (1- {\ Frac {v_ {\ ell}} {v_ {i}}} \ prawej) \\& = C_ { C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/ A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\right)\ .\\\end{aligned}}}$

(Dla dodatniej pojemności Millera, A _v jest ujemne.) Po podstawieniu tego wyniku do wyrażenia wzmocnienia i zbierania składników, wzmocnienie jest przepisywane jako:

${\ Displaystyle {\ Frac {v _ {\ ell}}} {v_ {a}}}=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}{\frac {R_{L}}{R_{L}+R_{o} }}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{D_{\omega}}}\ ,}$

z D _ω określonym przez kwadrat w ω, a mianowicie:

${\ Displaystyle D _ {\ omega} \ \!}$${\ Displaystyle = [1 + j \ omega (C_ {L } + C_ {C}) (R_ {o} \ | R_ {L})] \, \!} ⋅ [ 1 + jot ω do$$1+ j\omega C_{i}(R_{A}\|R_{i})]\,\!}$ ${\ Displaystyle \ + j \ omega C_ {C} (R_ {A} \ | R_ {i}) \ \!}$${\ Displaystyle \ cdot \ lewo (1-A_ {v} {\ Frac {R_ {L}} {R_ {L} + R_ {O}}} \ prawej) \, \!}$${\ Displaystyle \ + (j \ omega) ^ {2} C_ {C} C_ {L} (R_ {A} \ | R_ {i}) (R_ {O} \| R_ {L}) \ .}$

Każdy kwadrat ma dwa dzielniki, a to wyrażenie wygląda na prostsze, jeśli zostanie zapisane jako

${\ Displaystyle \ D _ {\ omega} = (1 + j \ omega {\ tau} _ {1}) (1 + j \ omega {\tau}_ {2})}$

${\ Displaystyle = 1 + j \ omega ({\ tau} _ {1} + {\ tau} _ {2}}) + (j \ omega) ^ {2} \ tau _ {1} \ tau _ {2 }\ ,\ }$

gdzie i $są$ D _kombinacjami pojemności i $.$ na Odpowiadają one stałym czasowym dwóch biegunów wzmacniacza. Jedna lub druga stała czasowa jest najdłuższa; załóżmy, że $1$ stałą czasową, odpowiadającą najniższemu biegunowi, i załóżmy, że $Displaystyle \ tau _ {1}}$ >> ${\ Displaystyle \ tau _ {2}}$ . (Dobra reakcja krokowa wymaga ${\ displaystyle \ tau _ {1}}$ >> ${\ displaystyle \ tau _ {2}}$ . Zobacz Wybór C _C poniżej.)

Przy niskich częstotliwościach w pobliżu najniższego bieguna tego wzmacniacza, zwykle człon liniowy w ω jest ważniejszy niż człon kwadratowy, więc zachowanie D _{ω przy niskich częstotliwościach} jest następujące:

${\ Displaystyle {\ rozpocząć {wyrównane} \ D _ {\ omega} i = 1 + j \ omega [(C_ {M} + C_ {i}) (R_ {A} \| R_ {i} )+(C_{L}+C_{C})(R_{o}\|R_{L})]\\&=1+j\omega (\tau _{1}+\tau _{2}) \około 1+j\omega \tau _{1}\ ,\ \\\end{wyrównane}}}$

gdzie teraz C _M jest przedefiniowane przy użyciu przybliżenia Millera jako

$\ Displaystyle C_ {M} = C_ {C} \ lewo (1-A_ {v}} {\ Frac {R_ {L}}} R_{L}+R_{o}}}\prawo)\ ,}$

która jest po prostu poprzednią pojemnością Millera ocenianą przy niskich częstotliwościach. Na tej podstawie określa się, pod warunkiem, że $Displaystyle$$\ tau _ {1}}$ >> ${2}}$ . Ponieważ C _{M jest duża,} $.$ czasowa jest znacznie większa niż jej pierwotna wartość do _ja ( R ZA _| R _ja )

Przy wysokich częstotliwościach człon kwadratowy staje się ważny. Zakładając, że powyższy wynik dla jest ważny, drugą stałą czasową, położenie bieguna wysokiej częstotliwości, oblicza się z wyrażenia kwadratowego w D _ω jako τ ${\ displaystyle \ tau _ {1}$

${\ Displaystyle \ tau _ {2} = {\ Frac {\ tau _ {1} \ tau _ {2}} {\ tau _ {1}}} \ około {\ Frac {\ tau _ {1} \ tau _{2}}{\tau _{1}+\tau_{2}}}\ .}$

$_ {1}}$ kwadratowy odpowiadający iloczynowi wraz $\ Displaystyle \$ oszacowaniem dla { znaleziono oszacowanie położenia drugiego bieguna:

${\ Displaystyle {\ rozpocząć {wyrównane} \ tau _ {2} & = {\ Frac {(C_ {C} C_ {L} + C_ {L} C_ {i} + C_ {i} C_ {C}) ( R_{A}\|R_{i})(R_{O}\|R_{L})}{(C_{M}+C_{i})(R_{A}\|R_{i})+( C_{L}+C_{C})(R_{o}\|R_{L})}}\\&\około {\frac {C_{C}C_{L}+C_{L}C_{i} +C_{i}C_{C}}{C_{M}}}(R_{O}\|R_{L})\ ,\\\koniec{wyrównany}}}$

a ponieważ C _M jest duży, wydaje się, że $jego$ R _rozmiar jest zmniejszony w stosunku do pierwotnej wartości C _L ( | R _L ); to znaczy, że wyższy biegun przesunął się jeszcze wyżej z częstotliwością z powodu C _C .

Krótko mówiąc, wprowadzenie kondensatora C _C przesunęło niski biegun w dół, a wysoki w górę, więc termin rozszczepienie biegunów wydaje się dobrym opisem.

Wybór _C.C

Rysunek 3: Wyidealizowany wykres Bode dla projektu wzmacniacza dwubiegunowego. Spadki wzmocnienia od pierwszego bieguna przy f ₁ przy 20 dB / dekadę do drugiego bieguna przy f ₂ , gdzie nachylenie wzrasta do 40 dB / dekadę.

Jaka wartość jest dobrym wyborem dla C _C ? Do zastosowań ogólnych, tradycyjna konstrukcja (często nazywana bieguna dominującego lub kompensacją jednobiegunową ) wymaga spadku wzmocnienia wzmacniacza o 20 dB na dekadę od częstotliwości narożnej do wzmocnienia 0 dB lub nawet niższego. Dzięki tej konstrukcji wzmacniacz jest stabilny i ma prawie optymalną odpowiedź skokową, nawet jako bufor napięciowy o wzmocnieniu równym jedności. Bardziej agresywną techniką jest kompensacja dwubiegunowa.

Droga do położenia f2 w celu _uzyskania projektu jest pokazana na rysunku 3. Na najniższym biegunie f1 wykres wzmocnienia Bodego załamuje zbocze opadające przy 20 dB/dekada _. Celem jest utrzymanie nachylenia 20 dB/dekadę aż do zera dB i przyjęcie stosunku pożądanego spadku wzmocnienia (w dB) o 20 log 10 A _v do _wymaganej zmiany częstotliwości (na logarytmie częstotliwości skala) z ( log ₁₀ fa ₂ − log ₁₀ fa ₁ ) = log ₁₀ ( fa ₂ / f ₁ ) nachylenie odcinka między f ₁ a f ₂ wynosi:

Nachylenie na dekadę częstotliwości ${\ Displaystyle = 20 {\ Frac {\ operatorname {log_ {10}} (A_ {v}) }{\mathrm {log_{10}} (f_{2}/f_{1})}}\ ,}$

czyli 20 dB/dekadę pod _{warunkiem ,} że f2 = _Avf1 . Jeśli f ₂ nie jest tak duże, druga przerwa w wykresie Bodego, która pojawia się na drugim biegunie, przerywa wykres, zanim wzmocnienie spadnie do 0 dB, co w konsekwencji spowoduje niższą stabilność i degradację odpowiedzi skokowej.

Rysunek 3 pokazuje, że aby uzyskać prawidłową zależność wzmocnienia od częstotliwości, drugi biegun ma co najmniej współczynnik Av _wyższą częstotliwość niż pierwszy biegun. Wzmocnienie jest nieco zmniejszone przez dzielniki napięcia na wejściu i wyjściu wzmacniacza, więc po korekcie A _v dla dzielników napięcia na wejściu i wyjściu warunek stosunku biegunów dla dobrej odpowiedzi skokowej wygląda następująco:

${\ Displaystyle {\ Frac {\ tau _ {1}} {\ tau _ {2}}} \ około A_ { v {\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,}$

Rysunek 4: Pojemność Millera przy niskich częstotliwościach C _M (góra) i kondensator kompensacyjny C _C (dół) jako funkcja wzmocnienia przy użyciu Excela . Jednostką pojemności jest pF.

Korzystając z przybliżeń dla stałych czasowych opracowanych powyżej,

${\ Displaystyle {\ Frac {\ tau _ {1}} {\tau _{2}}}\około {\frac {(\tau _{1}+\tau _{2})^{2}}{\tau _{1}\tau _{2}}} \około A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}} \ ,}$

Lub

${\ Displaystyle {\ Frac {[(C_ {M} + C_ {i}) (R_ {A} \| R_ {i}) + (C_ {L} + C_ {C })(R_{o}\|R_{L})]^{2}}{(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})( R_ {A}\|R_{i})(R_{O}\|R_{L})}}\,\!}$${\ Displaystyle {\ kolor {biały} \ cdot} = A_ {v} {\ Frac {R_ {i}} {R_ {i} + R_ {A}}} \ cdot {\ Frac {R_ {L}} R_{L}+R_{o}}}\ ,}$

który zapewnia równanie kwadratowe w celu określenia odpowiedniej wartości dla C _C . Rysunek 4 przedstawia przykład zastosowania tego równania. Przy niskich wartościach wzmocnienia ten przykładowy wzmacniacz spełnia warunek stosunku biegunów bez kompensacji (czyli na rysunku 4 kondensator kompensacyjny C _C jest mały przy niskim wzmocnieniu), ale wraz ze wzrostem wzmocnienia szybko staje się konieczna pojemność kompensacyjna (tzn. na rysunku 4 kondensator kompensacyjny CC wzrasta szybko wraz ze wzmocnieniem) _, ponieważ niezbędny stosunek biegunów wzrasta wraz ze wzmocnieniem. Aby uzyskać jeszcze większy zysk, niezbędne C _C spada wraz ze wzrostem wzmocnienia, ponieważ wzmocnienie CC Millera _mniejszą CC _, które wzrasta wraz ze wzmocnieniem (patrz równanie Millera ), pozwala na wartość .

prawej _{Aby zapewnić większy margines bezpieczeństwa dla niepewności projektowych, często Av} tego _{zwiększa się do dwu- lub trzykrotnego Av} po stronie równania. Zobacz Sansen lub Huijsing i artykuł na temat odpowiedzi skokowej .

Szybkość narastania

Powyższe jest analizą małosygnałową. Jednakże, gdy używane są duże sygnały, potrzeba ładowania i rozładowywania kondensatora kompensacyjnego niekorzystnie wpływa na szybkość narastania wzmacniacza ; CC _w szczególności odpowiedź na wejściowy sygnał rampy jest ograniczona przez konieczność ładowania .

Zobacz też

• Kompensacja częstotliwości
• Efekt Millera
• Zasilanie główne
• Fabuła Bodego
• Odpowiedź krokowa
• Wzmacniacz CMOS

Linki zewnętrzne

• Wykresy Bode w Wikibook Teoria obwodów
• Działki Bode w Control Systems Wikibook