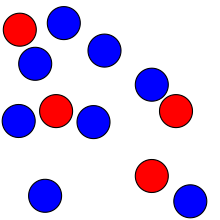
Podporządkowanie
Subityzacja to szybka, dokładna i pewna ocena liczb dokonywana dla niewielkiej liczby elementów. Termin został ukuty w 1949 roku przez EL Kaufmana i wsp. I wywodzi się od łacińskiego przymiotnika subitus (oznaczającego „nagły”) i oddaje poczucie natychmiastowej wiedzy, ile przedmiotów znajduje się w scenie wizualnej, kiedy liczba obecnych przedmiotów spada w zakresie subityzacji. Zestawów większych niż około cztery elementy nie można podzielić, chyba że elementy pojawiają się we wzorze znanym danej osobie (takim jak sześć kropek na jednej ściance kostki). Duże, znane zestawy mogą być liczone jeden po drugim (lub osoba może obliczyć liczbę za pomocą szybkiego obliczenia, jeśli potrafi mentalnie pogrupować elementy w kilka małych zestawów). Osoba może również oszacować liczbę dużego zestawu - umiejętność podobna do dzielenia na części, ale różniąca się od niej.
Dokładność, szybkość i pewność, z jaką obserwatorzy dokonują oceny liczby elementów, są w dużym stopniu zależne od liczby elementów do wyliczenia. Oceny dokonane w przypadku ekspozycji składających się z około jednego do czterech elementów są szybkie, dokładne i pewne. Jednak gdy do policzenia jest więcej niż cztery elementy, oceny są dokonywane z malejącą dokładnością i pewnością. Ponadto czasy reakcji rosną dramatycznie, dodając dodatkowe 250–350 ms dla każdego dodatkowego elementu na wyświetlaczu powyżej około czterech.
Podczas gdy wzrost czasu odpowiedzi dla każdego dodatkowego elementu na wyświetlaczu wynosi 250–350 ms na element poza zakresem podziału na części, nadal istnieje znaczny, choć mniejszy wzrost o 40–100 ms na element w zakresie podziału na części. Podobny wzór czasów reakcji występuje u małych dzieci, chociaż z bardziej stromymi zboczami zarówno dla zakresu subityzacji, jak i zakresu wyliczania. Sugeruje to, że nie ma rozpiętości obaw jako takie, jeśli jest to zdefiniowane jako liczba elementów, które mogą być natychmiast uchwycone przez procesy poznawcze, ponieważ z każdym dodatkowym wyliczonym elementem wiąże się dodatkowy koszt. Jednak względne różnice w kosztach związanych z wyliczaniem pozycji w zakresie subityzacji są niewielkie, niezależnie od tego, czy są mierzone pod względem dokładności, pewności, czy szybkości odpowiedzi . Co więcej, wartości wszystkich miar wydają się znacznie różnić wewnątrz i na zewnątrz zakresu subityzacji. Tak więc, chociaż może nie być rozpiętości obaw, wydają się istnieć rzeczywiste różnice w sposobach, w jakie niewielka liczba elementów jest przetwarzana przez system wizualny (tj. około czterech lub mniej elementów), w porównaniu z większą liczbą elementów (tj. w przybliżeniu więcej niż cztery pozycje).
Badanie z 2006 roku wykazało, że subityzacja i liczenie nie ograniczają się do percepcji wzrokowej, ale obejmują również percepcję dotykową, kiedy obserwatorzy musieli nazwać liczbę stymulowanych opuszek palców. Badanie z 2008 roku wykazało również zastępowanie i liczenie w percepcji słuchowej. Chociaż kwestionowano istnienie subityzacji w percepcji dotykowej, efekt ten był wielokrotnie powtarzany i dlatego można go uznać za solidny. Efekt subityzowania uzyskano również w percepcji dotykowej u dorosłych niewidomych od urodzenia. Łącznie odkrycia te wspierają ideę, że subityzacja jest ogólnym mechanizmem percepcyjnym rozciągającym się na przetwarzanie słuchowe i dotykowe.
Wyliczanie powidoków
Jak sugeruje pochodzenie terminu „subityzacja”, uczucie związane z dokonaniem oceny liczbowej w zakresie subityzacji polega na natychmiastowym uświadomieniu sobie wyświetlanych elementów. Gdy liczba prezentowanych obiektów przekracza zakres subityzacji, to uczucie zanika, a obserwatorzy często zgłaszają wrażenie przesuwania punktu widzenia wokół wyświetlacza, aż do policzenia wszystkich prezentowanych elementów. Zdolność obserwatorów do zliczania liczby elementów na wyświetlaczu może być ograniczona przez szybką prezentację i późniejsze maskowanie elementów lub wymaganie od obserwatorów szybkiej reakcji. Obie procedury mają niewielki, jeśli w ogóle, wpływ na wyliczanie w zakresie subityzacji. Techniki te mogą ograniczać zdolność obserwatorów do liczenia przedmiotów, ograniczając stopień, w jakim obserwatorzy mogą kolejno przesuwać swoją „strefę uwagi” na różne elementy na wyświetlaczu.
Atkinson, Campbell i Francis wykazali, że powidoki wizualne można wykorzystać do osiągnięcia podobnych rezultatów. Używając lampy błyskowej do oświetlenia linii białych dysków, byli w stanie wygenerować intensywne powidoki u obserwatorów przystosowanych do ciemności. Obserwatorzy byli zobowiązani do ustnego zgłaszania, ile dysków zostało przedstawionych, zarówno po 10, jak i po 60 sekundach od ekspozycji z lampy błyskowej. Obserwatorzy zgłosili, że byli w stanie zobaczyć wszystkie prezentowane dyski przez co najmniej 10 s i byli w stanie dostrzec przynajmniej niektóre z dysków po 60 S. W przeciwieństwie do zwykłego wyświetlania obrazów w odstępach 10 i 60 sekund, gdy są one prezentowane w formie powidoków, ruchy gałek ocznych nie mogą być wykorzystywane do liczenia: kiedy badani poruszają oczami, obrazy również się poruszają. Pomimo długiego czasu na wyliczenie liczby przedstawionych dysków, gdy liczba przedstawionych dysków wypadła poza zakres podziału na części (tj. 5–12 dysków), obserwatorzy popełniali spójne błędy wyliczania zarówno w warunkach 10 s, jak i 60 s . W przeciwieństwie do tego, nie wystąpiły żadne błędy w zakresie subityzacji (tj. 1–4 dysków), ani w warunkach 10 s, ani 60 s.
Struktury mózgu zaangażowane w subityzację i liczenie
Praca nad wyliczaniem powidoków potwierdza pogląd, że różne procesy poznawcze służą do wyliczania elementów wewnątrz i na zewnątrz zakresu subityzacji, i jako takie stwarzają możliwość, że subityzacja i liczenie obejmują różne obwody mózgowe. Jednak obrazowania funkcjonalnego zostały zinterpretowane zarówno w celu wspierania różnych, jak i wspólnych procesów.
zespół Bálinta
Dowody kliniczne potwierdzające pogląd, że subityzacja i liczenie mogą obejmować funkcjonalnie i anatomicznie odrębne obszary mózgu, pochodzą od pacjentów z jednoczesną gnozją , jedną z kluczowych składowych zespołu Bálinta . Pacjenci z tym zaburzeniem cierpią na niezdolność do prawidłowego postrzegania scen wizualnych, nie są w stanie zlokalizować obiektów w przestrzeni, czy to poprzez patrzenie na przedmioty, wskazywanie na nie, czy ustne zgłaszanie ich położenia. Mimo tych dramatycznych objawów tacy pacjenci są w stanie poprawnie rozpoznać poszczególne obiekty. Co najważniejsze, osoby z symultanagnozją nie są w stanie wyliczyć obiektów poza zakresem subityzacji, albo nie potrafią policzyć niektórych obiektów, albo alternatywnie liczą ten sam obiekt kilka razy.
Jednak osoby z symultanagnozją nie mają trudności z wyliczaniem obiektów w zakresie subityzacji. Zaburzenie jest związane z obustronnym uszkodzeniem płata ciemieniowego , obszaru mózgu związanego z przestrzennymi przesunięciami uwagi. Te wyniki neuropsychologiczne są zgodne z poglądem, że proces liczenia, ale nie subityzowania, wymaga aktywnego przesunięcia uwagi. Jednak ostatnie badania zakwestionowały ten wniosek, stwierdzając, że uwaga wpływa również na zastępowanie.
Wyliczanie obrazu
Dalsze źródło badań nad neuronowymi procesami subityzacji w porównaniu do liczenia pochodzi z badań pozytonowej tomografii emisyjnej (PET) na zwykłych obserwatorach. Takie badanie porównuje aktywność mózgu związaną z procesami wyliczania wewnątrz (tj. 1–4 pozycji) w celu dzielenia na podpunkty i na zewnątrz (tj. 5–8 pozycji) w przypadku liczenia.
Takie badania pokazują, że w zakresie subityzacji i liczenia aktywacja zachodzi obustronnie w korze potylicznej ekstraprążkowia i górnym płacie ciemieniowym / bruździe śródciemieniowej. Zostało to zinterpretowane jako dowód, że zaangażowane są wspólne procesy. Jednak istnienie dalszych aktywacji podczas liczenia w prawych dolnych obszarach czołowych i przednim zakręcie zostało zinterpretowane jako sugerujące istnienie odrębnych procesów podczas liczenia związanych z aktywacją regionów zaangażowanych w przenoszenie uwagi.
Aplikacje edukacyjne
Historycznie rzecz biorąc, wiele systemów próbowało użyć subityzacji do identyfikacji pełnych lub częściowych ilości. W XX wieku nauczyciele matematyki zaczęli stosować niektóre z tych systemów, jak przedstawiono w poniższych przykładach, ale często przestawiali się na bardziej abstrakcyjne kodowanie kolorami, aby reprezentować wielkości do dziesięciu.
W latach 90. wykazano, że trzytygodniowe niemowlęta rozróżniają 1–3 obiekty, czyli podporządkowują. Nowsze meta-badanie podsumowujące pięć różnych badań wykazało, że niemowlęta rodzą się z wrodzoną zdolnością do różnicowania ilości w niewielkim zakresie, który zwiększa się z czasem. W wieku siedmiu lat ta zdolność wzrasta do 4–7 przedmiotów. Niektórzy praktycy twierdzą, że dzięki szkoleniu dzieci są w stanie poprawnie zamienić obiekty powyżej 15 lat. [ potrzebne źródło ]
Liczydło
Hipotetyczne użycie yupany , systemu liczenia Inków, umieszczało do pięciu liczników w połączonych tacach do obliczeń.
W każdej wartości miejsca chińskie liczydło używa czterech lub pięciu koralików do reprezentowania jednostek, które są podpisane, oraz jednego lub dwóch oddzielnych koralików, które symbolizują piątki. Pozwala to na wykonywanie wielocyfrowych operacji, takich jak przenoszenie i pożyczanie, bez subityzacji powyżej pięciu.
Liczydła europejskie używają dziesięciu koralików w każdym rejestrze, ale zwykle dzielą je na piątki według koloru.
Narzędzia dydaktyczne XX wieku
Idea natychmiastowego rozpoznawania wielkości została przyjęta przez kilka systemów pedagogicznych, takich jak Montessori , Cuisenaire i Dienes . Jednak systemy te tylko częściowo wykorzystują subityzację, starając się, aby wszystkie wielkości od 1 do 10 były natychmiast rozpoznawalne. Aby to osiągnąć, kodują ilości według koloru i długości reprezentujących je prętów lub sznurków koralików. Rozpoznawanie takich wizualnych lub dotykowych reprezentacji i kojarzenie z nimi ilości wymaga innych operacji umysłowych niż podporządkowanie.
Inne aplikacje
Jednym z najbardziej podstawowych zastosowań jest grupowanie cyfr w duże liczby, które pozwalają na określenie rozmiaru na pierwszy rzut oka, zamiast konieczności liczenia. Na przykład zapisanie jednego miliona (1000000) jako 1 000 000 (lub 1 000 000 lub 1 000 000 ) lub jednego ( krótkiego ) miliarda (1 000 000 000) jako 1 000 000 000 (lub innych form, takich jak 1 00 00 00 000 w numeracji indyjskiej system ) znacznie ułatwia czytanie. Jest to szczególnie ważne w księgowości i finansach, ponieważ błąd jednej cyfry dziesiętnej zmienia kwotę dziesięciokrotnie. Znajduje się to również w komputerze języki programowania dla wartości literalnych ; zobacz literał całkowity § Separatory cyfr .
Kości , karty do gry i inne urządzenia do gier tradycyjnie dzielą ilości na grupy, które można podzielić na części, z rozpoznawalnymi wzorami. Behawioralna zaleta tej metody grupowania została naukowo zbadana przez Ciccione i Dehaene , którzy wykazali, że wyniki liczenia są lepsze, jeśli grupy dzielą tę samą liczbę elementów i ten sam powtarzalny wzór.
Porównywalnym zastosowaniem jest dzielenie reprezentacji liczb binarnych i szesnastkowych, numerów telefonów, numerów kont bankowych (np. IBAN , numery PESEL, tablice rejestracyjne itp.) lub inne separatory. Ma to na celu wsparcie nadzorowania kompletności liczby podczas porównywania lub ponownego wpisywania. Ta praktyka grupowania znaków ułatwia również zapamiętywanie dużych liczb i struktur znaków.
Samoocena
Istnieje co najmniej jedna gra, w którą można grać online, aby samodzielnie ocenić swoją zdolność do podporządkowania się.