Tasowanie Faro

Faro shuffle (amerykański), weave shuffle (brytyjski) lub tasowanie jaskółczego ogona to metoda tasowania kart do gry , w której połowa talii jest trzymana w każdej ręce z kciukami do wewnątrz, a następnie karty są uwalniane przez kciuki tak, że spadają na stół przeplatane. Diaconis, Graham i Kantor nazywają to również techniką używaną w magii.

Porównanie doskonałego faro out-shuffle i in-shuffle, liczby oznaczające pozycje każdej karty przed tasowaniem

Matematycy używają terminu „przetasowanie faro”, aby opisać precyzyjne przegrupowanie talii na dwa równe stosy po 26 kart, które następnie są idealnie przeplatane.

Opis

Praworęczny praktykujący trzyma karty od góry w lewej ręce i od dołu w prawej ręce. Talia jest podzielona na dwie, najlepiej równe części, po prostu lekko podnosząc połowę kart prawym kciukiem i odsuwając pakiet lewej ręki od prawej ręki. Te dwa pakiety są często krzyżowane i uderzane o siebie, aby je wyrównać. Następnie są one zsuwane razem na krótszych bokach i wyginane w górę lub w dół. Karty będą wtedy naprzemiennie opadać na siebie, najlepiej naprzemiennie jedna po drugiej z każdej połowy, podobnie jak zamek błyskawiczny . Zawijas może być dodany poprzez sprężyste pakiety razem poprzez wywieranie nacisku i zginanie ich od góry.

Gra w Faro kończy się dwoma równymi stosami kart, które krupier musi połączyć, aby rozdać je w następnej grze. Według maga Johna Maskelyne'a zastosowano powyższą metodę, którą nazywa „tasowaniem rozdającego faro”. Maskelyne był pierwszym, który dał jasne instrukcje, ale tasowanie było używane i kojarzone z faro wcześniej, co odkrył głównie matematyk i magik Persi Diaconis .

Idealne przetasowania

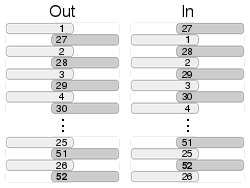
Tasowanie faro, które pozostawia oryginalną górną kartę na górze, a oryginalną dolną kartę na dole, jest znane jako out-shuffle , podczas gdy takie, które przesuwa oryginalną górną kartę na drugą, a oryginalną dolną kartę na drugą od dołu, jest znane jako przetasowanie . Nazwy te zostały ukute przez magika i programistę komputerowego Alexa Elmsleya . Idealne tasowanie faro, w którym karty są idealnie ułożone naprzemiennie, wymaga od tasującego podzielenia talii na dwa równe stosy i zastosowania odpowiedniego nacisku podczas spychania połówek talii jedna na drugą.

Tasowanie faro to kontrolowane tasowanie, w którym talia nie jest w pełni losowa. Jeśli ktoś potrafi wykonać perfekcyjne tasowanie, 26 tasowań odwróci kolejność talii, a kolejne 26 przywróci jej pierwotną kolejność.

Ogólnie rzecz biorąc, doskonałe $tasowanie$ przywróci porządek talii $Displaystyle$ , jeśli $2 ^ {k} \ równoważnik 1 {\pmod {n+1}}}$ . Na przykład 52 kolejne przetasowania przywracają kolejność talii 52 kart, ponieważ ${\ Displaystyle 2 ^ {52} \ equiv 1 {\ pmod {53}}}$ .

Ogólnie rzecz biorąc, $idealne$ przetasowanie przywróci porządek talii $kart$ , jeśli ${\ Displaystyle 2 ^ {k} \$ . Na przykład, jeśli uda się wykonać osiem przetasowań z rzędu, talia 52 kart zostanie przywrócona do pierwotnej kolejności, ponieważ ${\ Displaystyle 2 ^ {8} \ równoważnik 1 {\pmod {51}}}$ . Jednak tylko 6 faro out-shuffle jest wymaganych do przywrócenia porządku w talii 64 kart.

Innymi słowy, liczba tasowań wymaganych do przywrócenia talii kart o parzystym rozmiarze N do pierwotnego porządku jest określona przez multiplikatywny rząd 2 modulo ( N + 1).

Na przykład dla talii o rozmiarze N = 2, 4, 6, 8, 10, 12 ... liczba potrzebnych przetasowań to: 2, 4, 3, 6, 10, 12, 4, 8, 18 , 6, 11, ... (sekwencja A002326 w OEIS ).

Zgodnie z przypuszczeniem Artina na temat prymitywnych korzeni , wynika z tego, że istnieje nieskończenie wiele rozmiarów talii, które wymagają pełnego zestawu n przetasowań.

Operacją analogiczną do out shuffle dla nieskończonej sekwencji jest sekwencja przeplotu .

Przykład

Dla uproszczenia użyjemy talii sześciu kart.

Poniżej przedstawiono kolejność talii po każdym przetasowaniu lub przetasowaniu. Zwróć uwagę, że talia tej wielkości powraca do swojej pierwotnej kolejności po 3 w tasowaniu.

Krok	Górna karta	2	3	4	5	Dolna karta
Początek
1
2
3

Poniżej przedstawiono kolejność talii po każdym tasowaniu. Zwróć uwagę, że talia tej wielkości powraca do swojej pierwotnej kolejności po 4 przetasowaniach.

Krok	Górna karta	2	3	4	5	Dolna karta
Początek
1
2
3
4

Jako manipulacja talią

Magik Alex Elmsley odkrył ^{[ potrzebne źródło ]} , że kontrolowana seria tasowań wejściowych i wyjściowych może być wykorzystana do przesunięcia górnej karty talii w dowolne miejsce. Sztuczka polega na wyrażeniu żądanej pozycji karty jako liczby binarnej , a następnie przetasowaniu na wejściu dla każdej 1 i przetasowaniu na zewnątrz dla każdego 0.

Na przykład, aby przesunąć górną kartę w dół, tak aby znajdowało się nad nią dziesięć kart, wyraź liczbę dziesięć w systemie binarnym (1010 ₂ ). Wmieszaj się, wyjdź, wejdź, wyjdź. Rozdaj dziesięć kart z wierzchu talii; jedenasta będzie twoją oryginalną kartą. Zauważ, że nie ma znaczenia, czy liczbę dziesięć wyrażasz jako 1010 ₂ czy 00001010 ₂ ; wstępne tasowanie nie wpłynie na wynik, ponieważ tasowanie zawsze powoduje, że górna karta jest na wierzchu.

Aspekty teorii grup

W matematyce idealne przetasowanie można uznać za element grupy symetrycznej .

Mówiąc bardziej ogólnie, w idealnym tasowaniem jest permutacja, która dzieli zestaw na 2 stosy i przeplata je: ${\ displaystyle S_ {2n}}$

{\ Displaystyle S_ {2n}}

=

{\ Displaystyle {\ rozpocząć {pmatrix} 1 i 2 i 3 i 4 i \ cdots & 2n -1&2n\\1&n+1&2&n+2&\cdots &n&2n\end{pmacierz}}}

Innymi słowy, jest to mapa

{\ Displaystyle k \ mapsto {\ rozpocząć {przypadki} {\ Frac {k + 1} {2}} i k \ {\ tekst {nieparzysty}} \\ n+{\frac {k}{2}}&k\ {\text{parzyste}}\end{przypadki}}}

Analogicznie, $stosów$ permutacja $dzieli$ elementem zbiór na i

( ${\ Displaystyle (2, n)}$ -doskonałe tasowanie, oznaczone , $\ Displaystyle (2 2 , n )$ ( $1)} -$ ${\ Displaystyle (2, n)$ ${\ Displaystyle \ rho _ {n}}$ idealne tasowanie z $cyklem$ , więc znak to :

{\ Displaystyle {\ mbox {sgn}} (\ rho _ {n}) = (-1) ^ {n + 1} {\ mbox {sgn}} (\ rho _ {n-1}).}

Znak jest więc 4-okresowy:

{\ Displaystyle {\ mbox {sgn}} (\ rho _{n})=(-1)^{\lfloor n/2\rfloor }={\begin{przypadki}+1&n\równoważnik 0,1{\pmod {4}}\\-1&n\równoważnik 2, 3{\pmod {4}}\end{przypadki}}}

Kilka pierwszych doskonałych tasowań to: ${0}}$ $rho$ , a transpozycja to ${\ displaystyle \$ ${\ Displaystyle (23) \ w S_ {4}}$ .

Notatki

Diaconis, P .; Graham, RL ; Kantor WM (1983). „Matematyka doskonałych tasowań” (PDF) . Postępy w matematyce stosowanej . 4 (2): 175–196. doi : 10.1016/0196-8858(83)90009-X .

Ellis, J.; Wentylator, H.; Shallit, J. (2002). „Cykle permutacji Multiway Perfect Shuffle” (PDF) . Matematyka dyskretna i informatyka teoretyczna . 5 : 169-180. doi : 10.46298/dmtcs.308 . Źródło 26 grudnia 2013 r .

Maskelyne, John (1894). Sharps and Flats: kompletne ujawnienie tajemnic oszukiwania w grach losowych i zręcznościowych . Longmans, Green and Company . Źródło 26 grudnia 2013 r .

Morris, S. Brent (1998). Magiczne sztuczki, tasowanie kart i dynamiczne pamięci komputerowe . Stowarzyszenie Matematyczne Ameryki. ISBN 0-883-85527-5 . Źródło 26 grudnia 2013 r .

Kolata, Gina (kwiecień 1982). „Doskonałe przetasowania i ich związek z matematyką”. nauka . 216 (4545): 505–506. Bibcode : 1982Sci...216..505K . doi : 10.1126/science.216.4545.505 . PMID 17735734 .
Jain, Peiyush (maj 2008). „Prosty algorytm w miejscu dla tasowania” . arXiv : 0805.1598 [ cs.DS ].