Wieża Hanoi

Ten artykuł dotyczy matematycznej gry dyskowej. Jeśli chodzi o grę karcianą, zobacz Wieża Hanoy . Aby zapoznać się z wietnamskim wieżowcem, zobacz Keangnam Hanoi Landmark Tower .

Zestaw modeli Wieży Hanoi (z 8 dyskami)

Animowane rozwiązanie zagadki Wieża Hanoi dla T (4, 3)

Interaktywny wyświetlacz Wieża Hanoi w Muzeum Universum w Meksyku

Wieża Hanoi (zwana także Problemem Świątyni Benares lub Wieżą Brahmy lub Wieżą Lucasa , a czasami w liczbie mnogiej jako Wieże lub po prostu układanka piramidy ) to gra matematyczna lub układanka składająca się z trzech prętów i wielu dysków o różnych średnicach , który może wsunąć się na dowolny pręt. Zagadka zaczyna się od dysków ułożonych na jednym pręcie w kolejności malejącej wielkości, najmniejszy u góry, przybliżając w ten sposób stożkową kształt. Celem układanki jest przesunięcie całego stosu na ostatni pręt, przestrzegając następujących zasad:

1. Jednocześnie można przenosić tylko jeden dysk.
2. Każdy ruch polega na zabraniu górnego dysku z jednego ze stosów i umieszczeniu go na wierzchu innego stosu lub na pustym pręcie.
3. Żaden dysk nie może być umieszczony na dysku, który jest od niego mniejszy.

Z 3 dyskami układankę można rozwiązać w 7 ruchach. Minimalna liczba ruchów wymaganych do rozwiązania zagadki Wieża Hanoi to 2 ⁿ - 1, gdzie n to liczba krążków.

Pochodzenie

Układanka została sprowadzona na Zachód przez francuskiego matematyka Édouarda Lucasa w 1883 roku. Niemal natychmiast pojawiły się liczne mity dotyczące starożytnej i mistycznej natury układanki, w tym jeden o indyjskiej świątyni w Kashi Vishwanath , zawierającej duży pokój z trzema zniszczonymi przez czas w nim słupy, otoczone 64 złotymi dyskami. Wykonując polecenie starożytnej przepowiedni, bramini kapłani od tego czasu poruszają tymi dyskami zgodnie z niezmiennymi zasadami Brahmy. Dlatego zagadka jest również znana jako Wieża Brahmy . Według legendy, gdy ostatni ruch układanki zostanie zakończony, nastąpi koniec świata.

Gdyby legenda była prawdziwa i gdyby kapłani byli w stanie przenosić dyski z szybkością jednego dysku na sekundę, przy użyciu najmniejszej liczby ruchów, zajęłoby im to 2 64 ⁻ 1 sekundy, czyli mniej więcej 585 miliardów lat, czyli około 42 razy więcej niż obecny wiek wszechświata.

Istnieje wiele odmian tej legendy. Na przykład w niektórych przekazach świątynia jest klasztorem , a kapłani są mnichami . Świątynia lub klasztor mogą znajdować się w różnych miejscach, w tym w Hanoi , i mogą być związane z dowolną religią . W niektórych wersjach wprowadzane są inne elementy, takie jak fakt, że wieża powstała na początku świata, czy też to, że kapłani lub mnisi mogą wykonać tylko jeden ruch dziennie.

Rozwiązanie

W układankę można grać dowolną liczbą dysków, chociaż wiele wersji zabawek ma ich około 7 do 9. Minimalna liczba ruchów wymaganych do rozwiązania zagadki Wieża Hanoi to 2 ⁿ - 1 , gdzie n to liczba krążków. To jest dokładnie n- ^ta liczba Mersenne'a bez wymagań co do pierwszości.

Rozwiązanie iteracyjne

Animacja iteracyjnego algorytmu rozwiązującego problem z 6 dyskami

Prostym rozwiązaniem układanki z zabawkami jest naprzemienne ruchy między najmniejszym i nie najmniejszym elementem. Przesuwając najmniejszy element, zawsze przesuwaj go do następnej pozycji w tym samym kierunku (w prawo, jeśli początkowa liczba elementów jest parzysta, w lewo, jeśli początkowa liczba elementów jest nieparzysta). Jeśli w wybranym kierunku nie ma pozycji wieży, przesuń element na przeciwny koniec, ale następnie kontynuuj ruch we właściwym kierunku. Na przykład, jeśli zacząłeś od trzech kawałków, przesunąłbyś najmniejszy kawałek na przeciwny koniec, a następnie kontynuowałbyś w lewo. Kiedy kolej ma ruszyć nie najmniejszą figurę, jest tylko jeden legalny ruch. W ten sposób ułożysz układankę w jak najmniejszej liczbie ruchów.

Prostsze stwierdzenie rozwiązania iteracyjnego

Dla parzystej liczby dysków:

• wykonać legalny ruch między kołkami A i B (w dowolnym kierunku),
• wykonać legalny ruch między kołkami A i C (w dowolnym kierunku),
• wykonać legalny ruch między kołkami B i C (w dowolnym kierunku),
• powtarzaj do skutku.

Dla nieparzystej liczby dysków:

• wykonać legalny ruch między kołkami A i C (w dowolnym kierunku),
• wykonać legalny ruch między kołkami A i B (w dowolnym kierunku),
• wykonać legalny ruch między kołkami B i C (w dowolnym kierunku),
• powtarzaj do skutku.

wykonuje się łącznie 2 ^{n − 1 ruchów.}

Równoważne rozwiązanie iteracyjne

Inny sposób generowania unikalnego optymalnego rozwiązania iteracyjnego:

Ponumeruj dyski od 1 do n (od największego do najmniejszego).

• Jeśli n jest nieparzyste, pierwszy ruch jest od kołka A do kołka C.
• Jeśli n jest parzyste, pierwszy ruch jest od kołka A do kołka B.

Teraz dodaj te ograniczenia:

• Żaden nieparzysty dysk nie może być umieszczony bezpośrednio na nieparzystym dysku.
• Żaden parzysty dysk nie może być umieszczony bezpośrednio na parzystym dysku.
• Czasami będą dwa możliwe kołki: jeden będzie miał dyski, a drugi będzie pusty. Umieść krążek na niepustym kołku.
• Nigdy nie przesuwaj dysku dwa razy z rzędu.

Biorąc pod uwagę te ograniczenia po pierwszym ruchu, w każdej kolejnej turze jest tylko jeden legalny ruch.

Sekwencja tych unikalnych ruchów jest optymalnym rozwiązaniem problemu równoważnym opisanemu powyżej rozwiązaniu iteracyjnemu.

Rozwiązanie rekurencyjne

Ilustracja rekurencyjnego rozwiązania układanki Wieże Hanoi z 4 dyskami. W pliku SVG kliknij szary przycisk, aby go rozwinąć lub zwinąć

Kluczem do rozwiązania problemu rekurencyjnie jest rozpoznanie, że można go podzielić na zbiór mniejszych podproblemów, z których każdy ma zastosowanie do tej samej ogólnej procedury rozwiązywania, której szukamy , a następnie całkowite rozwiązanie można znaleźć w kilku prostych drogi od rozwiązań tych podproblemów. Każdy z tych utworzonych podproblemów, będąc „mniejszym”, gwarantuje, że przypadek podstawowy zostanie ostatecznie osiągnięty. Stąd dla Wież Hanoi:

• oznacz kołki A, B, C,
• niech n będzie całkowitą liczbą dysków,
• ponumeruj dyski od 1 (najmniejszy, najwyższy) do n (największy, najniższy).

Zakładając, że wszystkie n krążków jest rozmieszczonych w prawidłowych układach między kołkami; zakładając, że na kołku źródłowym znajduje się m dysków górnych , a wszystkie pozostałe dyski są większe niż m , więc można je bezpiecznie zignorować; przenieść m dysków z kołka źródłowego do kołka docelowego za pomocą zapasowego kołka, bez naruszania zasad:

1. Przenieś m − 1 krążków ze źródła na zapasowy kołek, stosując tę ​​samą ogólną procedurę rozwiązywania . Zasady nie są łamane, z założenia. Pozostawia to dysk m jako górny dysk na kołku źródłowym.
2. Przenieś dysk m od kołka źródłowego do docelowego , co z założenia jest prawidłowym ruchem — prosty krok .
3. Przenieś krążki m − 1, które właśnie umieściliśmy na kołku zapasowym, z kołka zapasowego na docelowy , stosując tę ​​samą ogólną procedurę rozwiązywania , tak aby zostały umieszczone na wierzchu krążka m bez naruszania zasad.
4. 0 Podstawowym przypadkiem jest przeniesienie dysków (w krokach 1 i 3), czyli nic nie robienie – co oczywiście nie łamie zasad.

Pełne rozwiązanie Wieży Hanoi polega następnie na przeniesieniu n dysków z kołka źródłowego A do kołka docelowego C, używając kołka B jako kołka zapasowego.

Podejście to można poddać rygorystycznemu dowodowi matematycznemu za pomocą indukcji matematycznej i jest często używane jako przykład rekurencji podczas nauczania programowania.

Analiza logiczna rozwiązania rekurencyjnego

Podobnie jak w przypadku wielu łamigłówek matematycznych, znalezienie rozwiązania jest łatwiejsze dzięki rozwiązaniu nieco bardziej ogólnego problemu: jak przesunąć wieżę h (wysokości) krążków z kołka początkowego f = A (z) na kołek docelowy t = C (do ), B jest pozostałym trzecim kołkiem i zakładając t ≠ f . Po pierwsze, zauważmy, że problem jest symetryczny dla permutacji nazw kołków ( grupa symetryczna S ₃ ). Jeśli rozwiązanie jest znane, przechodząc od kołka A na kołek C , a następnie zmieniając nazwy kołków, to samo rozwiązanie można zastosować do każdego innego wyboru kołka początkowego i docelowego. Jeśli jest tylko jeden dysk (lub w ogóle go nie ma), problem jest trywialny. Jeśli h = 1, po prostu przesuń krążek z kołka A na kołek C. Jeśli h > 1, to gdzieś w sekwencji ruchów największy krążek musi zostać przesunięty z kołka A na inny kołek, najlepiej na kołek C . Jedyna sytuacja, która pozwala na ten ruch, to sytuacja, w której wszystkie mniejsze krążki h − 1 znajdują się na kołku B . Dlatego najpierw wszystkie h − 1 mniejsze krążki muszą przejść z A do B . Następnie przenieś największy krążek i na koniec przenieś h − 1 krążków mniejszych z kołka B na kołek C . Obecność największego krążka nie przeszkadza żadnemu ruchowi mniejszych krążków o h − 1 i można go chwilowo zignorować. Teraz problem sprowadza się do przeniesienia h − 1 krążków z jednego kołka na drugi, najpierw z A do B , a następnie z B do C , ale tej samej metody można użyć za każdym razem, zmieniając nazwy kołków. Tej samej strategii można użyć do zredukowania h -1 do h -2, h -3 i tak dalej, aż pozostanie tylko jeden krążek. Nazywa się to rekurencją. Algorytm ten można przedstawić schematycznie w następujący sposób.

Zidentyfikuj dyski w kolejności rosnącego rozmiaru według liczb naturalnych od 0 do, ale nie wliczając h . Stąd krążek 0 jest najmniejszy, a krążek h − 1 największy.

Poniżej przedstawiono procedurę przenoszenia wieży h krążków z kołka A na kołek C , przy czym B jest pozostałym trzecim kołkiem:

1. Jeśli h > 1, najpierw użyj tej procedury, aby przesunąć krążki o h - 1 mniejsze z kołka A na kołek B .
2. Teraz największy krążek, czyli krążek h, można przesunąć z kołka A na kołek C.
3. Jeśli h > 1, to ponownie użyj tej procedury, aby przenieść krążki o h - 1 mniejsze z kołka B na kołek C .

Za pomocą indukcji matematycznej można łatwo udowodnić, że powyższa procedura wymaga minimalnej możliwej liczby ruchów i że otrzymane rozwiązanie jest jedynym z taką minimalną liczbą ruchów. Korzystając z relacji rekurencyjnych , dokładną liczbę ruchów wymaganych przez to rozwiązanie można obliczyć ze wzoru: ${\ Displaystyle 2 ^ {h} -1}$ . Wynik ten uzyskuje się, zauważając, że kroki 1 i 3 wykonują ${\ displaystyle T_ {h-1}}$ a krok 2 wykonuje jeden ruch, dając ${\ Displaystyle T_ {h} = 2T_ {h-1} + 1}$ .

Implementacja rekurencyjna

Poniższy kod w języku Python demonstruje rozwiązanie cykliczne.

    
  
  

    
       0
        
              A  =  [  3  ,  2  ,  1  ]  B  =  []  C  =  []  def  move  (  n  ,  source  ,  target  ,  pomocniczy  ):  if  n  >  :  # Przenieś n - 1 dysków ze źródła do pomocniczego, tak aby znalazły się poza sposób  ruchu  (  n  -  1  ,  źródło  ,  pomocniczy  ,  cel  ) 

        
        

        
            

        
              # Przenieś n-ty dysk ze źródła do  celu docelowego   .  append  (  source  .  pop  ()) # Wyświetl nasz   wydruk  postępu  (  A  ,  B  ,  C  ,  '##############'  ,  sep  =  '  \n  '  )  # Przenieś n - 1 dyski, które zostawiliśmy jako pomocnicze w celu  przeniesienia  (  n  -  1  ,  pomocnicze  ,  docelowe  ,  źródłowe 


    )  # Zainicjuj połączenie ze źródła A do celu C za pomocą pomocniczego  ruchu B   (  3  ,  A  ,  C  ,  B  ) 

Rozwiązanie nierekurencyjne

Lista ruchów wieży przenoszonej z jednego kołka na drugi, tworzona przez algorytm rekurencyjny, ma wiele prawidłowości. Licząc ruchy zaczynając od 1, liczba porządkowa dysku, który ma zostać przesunięty podczas ruchu m , jest liczbą razy m można podzielić przez 2. Stąd każdy nieparzysty ruch dotyczy najmniejszego dysku. Można również zauważyć, że najmniejszy krążek przechodzi przez kołki f , t , r , f , t , r , itd. dla nieparzystej wysokości wieży i przechodzi przez kołki f , r , t , f , r , t , itd. dla równej wysokości wieży. Zapewnia to następujący algorytm, który jest łatwiejszy do wykonania ręcznie niż algorytm rekurencyjny.

W ruchach alternatywnych:

• Przenieś najmniejszy krążek na kołek, z którego ostatnio nie pochodził.
• Przenieś legalnie kolejny dysk (będzie tylko jedna możliwość).

W pierwszym ruchu najmniejszy krążek trafia do kołka t, jeśli h jest nieparzyste, i do kołka r, jeśli h jest parzyste.

Należy również zauważyć, że:

• Dyski, których liczby porządkowe mają parzystą parzystość, poruszają się w tym samym kierunku, co najmniejszy dysk.
• Dyski, których liczby porządkowe mają nieparzystą parzystość, poruszają się w przeciwnym kierunku.
• Jeśli h jest parzyste, pozostałym trzecim kołkiem podczas kolejnych ruchów jest t , r , f , t , r , f , itd.
• Jeśli h jest nieparzyste, pozostały trzeci kołek podczas kolejnych ruchów to r , t , f , r , t , f , itd.

Dzięki tej wiedzy zestaw dysków w środku rozwiązania optymalnego można odzyskać bez informacji o stanie większej niż pozycje każdego dysku:

• Nazwij ruchy wyszczególnione powyżej „naturalnym” ruchem dysku.
• Zbadaj najmniejszy górny krążek, który nie jest krążkiem 0, i zanotuj, jaki byłby jego jedyny (legalny) ruch: jeśli nie ma takiego krążka, to jesteśmy albo w pierwszym, albo w ostatnim ruchu.
• Jeśli ten ruch jest „naturalnym” ruchem dysku, to dysk nie został poruszony od ostatniego ruchu dysku 0 i ten ruch powinien zostać wykonany.
• Jeśli ten ruch nie jest „naturalnym” ruchem dysku, przesuń dysk 0.

Rozwiązanie binarne

Pozycje dysków można określić bardziej bezpośrednio na podstawie binarnej (podstawa-2) reprezentacji numeru ruchu (stan początkowy to ruch nr 0, ze wszystkimi cyframi 0, a stan końcowy to wszystkie cyfry 1), stosując następujące zasady:

• jest jedna cyfra binarna ( bit ).
• Najbardziej znaczący (lewy) bit reprezentuje największy dysk. Wartość 0 wskazuje, że największy krążek znajduje się na początkowym kołku, podczas gdy 1 oznacza, że ​​jest na końcowym kołku (prawy kołek, jeśli liczba krążków jest nieparzysta, środkowy kołek w przeciwnym razie).
• Ciąg bitów jest odczytywany od lewej do prawej, a każdy bit może być użyty do określenia lokalizacji odpowiedniego dysku.
• Bit o tej samej wartości co poprzedni oznacza, że ​​odpowiedni dysk jest ułożony na poprzednim dysku na tym samym kołku.

  (To znaczy: prosta sekwencja jedynek lub zer oznacza, że ​​wszystkie odpowiednie krążki znajdują się na tym samym kołku.)

• Bit o innej wartości niż poprzedni oznacza, że ​​odpowiadający mu dysk znajduje się o jedną pozycję w lewo lub w prawo od poprzedniego. To, czy jest w lewo, czy w prawo, zależy od tej reguły:
  • Załóżmy, że początkowy kołek znajduje się po lewej stronie.
  • Załóżmy również „zawijanie” – więc prawy kołek liczy się jako jeden kołek „na lewo” od lewego kołka i odwrotnie.
  • Niech n będzie liczbą większych krążków, które znajdują się na tym samym kołku, co ich pierwszy większy krążek i dodaj 1, jeśli największy krążek znajduje się na lewym kołku. Jeśli n jest parzyste, krążek znajduje się o jeden kołek w prawo, jeśli n jest nieparzyste, krążek znajduje się o jeden kołek w lewo (w przypadku parzystej liczby krążków i odwrotnie).

Na przykład w 8-dyskowym Hanoi:

• Przenieś 0 = 00000000.
  • Największy dysk to 0, więc znajduje się na lewym (początkowym) kołku.
  • Wszystkie inne dyski również mają wartość 0, więc są ułożone na nim. Stąd wszystkie dyski są na początkowym kołku.
• Przenieś 2 ⁸ - 1 = 11111111.
  • Największy dysk to 1, więc znajduje się na środkowym (ostatnim) kołku.
  • Wszystkie pozostałe dyski również mają wartość 1, więc są ułożone na nim. Dlatego wszystkie krążki są na ostatnim kołku, a układanka jest kompletna.
• Przenieś 216 ₁₀ = 11011000.
  • Największy dysk to 1, więc znajduje się na środkowym (ostatnim) kołku.
  • Dysk drugi to również 1, więc jest ułożony na nim, na środkowym kołku.
  • Dysk trzeci to 0, więc jest na innym kołku. Ponieważ n jest nieparzyste ( n = 1), jest to jeden kołek w lewo, tj. na lewym kołku.
  • Dysk czwarty to 1, więc jest na innym kołku. Ponieważ n jest nieparzyste ( n = 1), jest to jeden kołek w lewo, czyli na prawym kołku.
  • Dysk piąty to również 1, więc jest ułożony na nim, na prawym kołku.
  • Krążek szósty to 0, więc jest na innym kołku. Ponieważ n jest parzyste ( n = 2), krążek znajduje się o jeden kołek w prawo, tj. na lewym kołku.
  • Dyski numer siedem i osiem również mają wartość 0, więc są ułożone na nim, na lewym kołku.

Kołki źródłowe i docelowe dla m -tego ruchu można również elegancko znaleźć z binarnej reprezentacji m za pomocą operacji bitowych . Aby użyć składni języka programowania C , przenieś m z peg (m & m - 1) % 3 do peg ((m | m - 1) + 1) % 3 , gdzie dyski zaczynają się na kołku 0 i kończą na kołek 1 lub 2 w zależności od tego, czy liczba krążków jest parzysta czy nieparzysta. Inne sformułowanie to peg (m - (m & -m)) % 3 do peg (m + (m & -m)) % 3 .

Ponadto dysk do przeniesienia jest określany na podstawie tego, ile razy licznik ruchów ( m ) można podzielić przez 2 (tj. liczbę bitów zerowych po prawej stronie), licząc pierwszy ruch jako 1 i identyfikując dyski za pomocą liczb 0, 1, 2 itd. w kolejności rosnącego rozmiaru. Pozwala to bardzo szybkiej nierekurencyjnej implementacji komputerowej na znalezienie pozycji dysków po m ruchach bez odniesienia do jakiegokolwiek poprzedniego ruchu lub dystrybucji dysków.

Operacja zliczania kolejnych zer na końcu liczby binarnej daje proste rozwiązanie problemu: krążki są numerowane od zera, a przy ruchu m liczba dysków kończących zer jest przesuwana na minimalną możliwą odległość do w prawo (w razie potrzeby obracając się z powrotem w lewo).

Rozwiązanie z kodem Graya

Binarny system liczbowy kodów Graya daje alternatywny sposób rozwiązania zagadki. W systemie Graya liczby są wyrażane w postaci binarnej kombinacji 0 i 1, ale kod Graya nie jest standardowym pozycyjnym systemem liczbowym , lecz opiera się na założeniu, że każda wartość różni się od swojej poprzedniczki tylko o jeden (i dokładnie jeden) bit zmienione.

Jeśli liczyć w kodzie Graya o rozmiarze bitowym równym liczbie dysków w określonej Wieży Hanoi, zaczynając od zera i licząc w górę, wówczas bit zmieniany przy każdym ruchu odpowiada dyskowi do przesunięcia, gdzie najmniej znaczący bit to najmniejszy dysk, a najbardziej znaczący bit jest największy.

Licząc ruchy od 1 i identyfikując dyski za pomocą liczb zaczynających się od 0 w kolejności rosnącego rozmiaru, liczba porządkowa dysku, który ma zostać przesunięty podczas ruchu m , to liczba razy m można podzielić przez 2.

Ta technika określa, który dysk należy przenieść, ale nie określa, gdzie go przenieść. W przypadku najmniejszego dysku zawsze istnieją dwie możliwości. W przypadku innych krążków zawsze istnieje jedna możliwość, z wyjątkiem sytuacji, gdy wszystkie krążki są na tym samym kołku, ale w takim przypadku albo najmniejszy krążek musi zostać przeniesiony, albo cel został już osiągnięty. Na szczęście istnieje zasada, która mówi, gdzie przenieść najmniejszy dysk. Niech f będzie kołkiem początkowym, t kołkiem docelowym, a r pozostałym trzecim kołkiem. Jeśli liczba krążków jest nieparzysta, najmniejszy krążek porusza się wzdłuż kołków w kolejności f → t → r → f → t → r , itd. Jeśli liczba krążków jest parzysta, należy to odwrócić: f → r → t → f → r → t , itd.

Pozycja zmiany bitu w rozwiązaniu kodu Graya podaje rozmiar dysku przesuwanego w każdym kroku: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, ... (sekwencja A001511 w OEIS ), sekwencja znana również jako funkcja linijki lub o jeden więcej niż potęga 2 w liczbie ruchu. W języku Wolfram IntegerExponent[Range[2^8 - 1], 2] + 1 daje ruchy dla 8-dyskowej układanki.

Reprezentacja graficzna

Główny artykuł: wykres Hanoi

Gra może być reprezentowana przez graf nieskierowany , węzły reprezentują rozkłady dysków, a krawędzie reprezentują ruchy. Dla jednego dysku wykres jest trójkątem:

Wykres dla dwóch dysków to trzy trójkąty połączone tak, aby tworzyły rogi większego trójkąta.

Dodawana jest druga litera reprezentująca większy dysk. Oczywiście początkowo nie można go przenieść.

Najwyższy mały trójkąt reprezentuje teraz możliwości jednego ruchu z dwoma dyskami:

Węzły w wierzchołkach najbardziej zewnętrznego trójkąta reprezentują rozkłady ze wszystkimi dyskami na tym samym kołku.

Dla dysków h + 1 weź wykres h dysków i zastąp każdy mały trójkąt wykresem dla dwóch dysków.

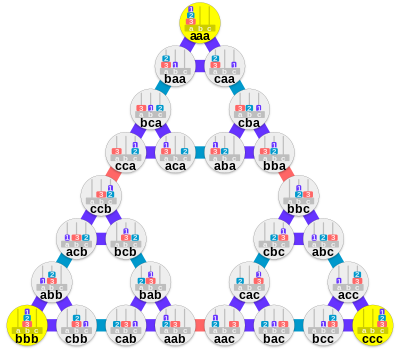
Dla trzech dysków wykres wygląda następująco:

Wykres gry poziomu 7 pokazuje pokrewieństwo z trójkątem Sierpińskiego .

• nazwij kołki a, b i c
• wyświetla pozycje dysków od lewej do prawej w kolejności rosnącego rozmiaru

Boki najbardziej zewnętrznego trójkąta reprezentują najkrótsze sposoby przenoszenia wieży z jednego kołka na drugi. Krawędź pośrodku boków największego trójkąta reprezentuje ruch największego dysku. Krawędź pośrodku boków każdego kolejnego mniejszego trójkąta reprezentuje ruch każdego kolejnego mniejszego krążka. Boki najmniejszych trójkątów reprezentują ruchy najmniejszego krążka.

Ogólnie rzecz biorąc, dla układanki z n dyskami na grafie jest 3 ^{n węzłów;} każdy węzeł ma trzy krawędzie do innych węzłów, z wyjątkiem trzech węzłów narożnych, które mają dwa: zawsze jest możliwe przesunięcie najmniejszego krążka do jednego z dwóch pozostałych kołków i możliwe jest przesunięcie jednego krążka między tymi dwoma kołkami, z wyjątkiem sytuacja, w której wszystkie krążki są ułożone na jednym kołku. Węzły narożne reprezentują trzy przypadki, w których wszystkie dyski są ułożone na jednym kołku. Diagram dla n + 1 dysków uzyskuje się, biorąc trzy kopie n -diagram dysku — każdy z nich reprezentuje wszystkie stany i ruchy mniejszych dysków dla jednej określonej pozycji nowego największego dysku — i łączy je w rogach trzema nowymi krawędziami, reprezentującymi tylko trzy możliwości przesunięcia największego dysku. Wynikowa figura ma zatem 3 ^{n +1} węzłów i nadal ma trzy pozostałe rogi z tylko dwiema krawędziami.

W miarę dodawania kolejnych dysków wykres przedstawiający grę będzie przypominał figurę fraktalną , trójkąt Sierpińskiego . Oczywiste jest, że zdecydowana większość pozycji w układance nigdy nie zostanie osiągnięta przy użyciu najkrótszego możliwego rozwiązania; rzeczywiście, jeśli kapłani z legendy użyją najdłuższego możliwego rozwiązania (bez ponownego odwiedzania jakiejkolwiek pozycji), zajmie im to 3 ⁶⁴ − 1 ruch, czyli więcej niż 10 ²³ lat.

Najdłuższy niepowtarzający się sposób dla trzech dysków można zwizualizować, usuwając nieużywane krawędzie:

Nawiasem mówiąc, tę najdłuższą, nie powtarzającą się ścieżkę można uzyskać, zabraniając wszelkich ruchów od a do c .

Cykl Hamiltona dla trzech dysków to:

Wykresy wyraźnie pokazują, że:

• Z każdego dowolnego rozmieszczenia krążków istnieje dokładnie jeden najkrótszy sposób przeniesienia wszystkich krążków na jeden z trzech kołków.
• Pomiędzy każdą parą dowolnych rozkładów dysków jest jedna lub dwie różne najkrótsze ścieżki.
• Z każdego dowolnego rozmieszczenia krążków istnieje jedna lub dwie najdłuższe, nieskrzyżowane ścieżki, którymi można przenieść wszystkie krążki na jeden z trzech kołków.
• Pomiędzy każdą parą dowolnych rozkładów dysków znajduje się jedna lub dwie różne najdłuższe nie przecinające się ścieżki.
• Niech Nh będzie liczbą nieprzecinających się ścieżek, którymi można przesunąć wieżę h krążków z jednego kołka _na drugi. Następnie:
  • N ₁ = 2
  • N _{godz +1} = ( N _godz ) ² + ( N _godz ) ³

Daje to N _h równe 2, 12, 1872, 6563711232, ... (sekwencja A125295 w OEIS )

Wariacje

Sąsiednie kołki

Jeśli wszystkie ruchy muszą odbywać się między sąsiednimi kołkami (tj. biorąc pod uwagę kołki A, B, C, nie można poruszać się bezpośrednio między kołkami A i C), to przesunięcie stosu n krążków z kołka A na kołek C wymaga 3 ⁿ − 1 ruchów. Rozwiązanie wykorzystuje wszystkie 3 ⁿ ważnych pozycji, zawsze wykonując unikalny ruch, który nie cofa poprzedniego ruchu. Pozycja ze wszystkimi krążkami na kołku B zostaje osiągnięta w połowie, czyli po (3 ⁿ − 1) / 2 ruchach.

Cykliczne Hanoi

W Cyclic Hanoi dostajemy trzy kołki (A, B, C), które są ułożone jako okrąg, przy czym kierunki zgodne z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara są zdefiniowane odpowiednio jako A – B – C – A i A – C – B – A. Kierunek ruchu dysku musi być zgodny z ruchem wskazówek zegara. Wystarczy przedstawić kolejność dysków do przeniesienia. Rozwiązanie można znaleźć za pomocą dwóch wzajemnie rekurencyjnych procedur:

Aby przenieść n dysków w kierunku przeciwnym do ruchu wskazówek zegara do sąsiedniego kołka docelowego:

1. przesuń n − 1 krążków w kierunku przeciwnym do ruchu wskazówek zegara do docelowego kołka
2. przesuń dysk # n o jeden krok w prawo
3. przesuń n − 1 krążków zgodnie z ruchem wskazówek zegara do kołka startowego
4. przesuń dysk # n o jeden krok w prawo
5. przesuń n − 1 krążków w kierunku przeciwnym do ruchu wskazówek zegara do docelowego kołka

Aby przenieść n dysków zgodnie z ruchem wskazówek zegara do sąsiedniego kołka docelowego:

1. przesuń n − 1 krążków przeciwnie do ruchu wskazówek zegara na zapasowy kołek
2. przesuń dysk # n o jeden krok w prawo
3. przesuń n − 1 krążków w kierunku przeciwnym do ruchu wskazówek zegara do docelowego kołka

Niech C(n) i A(n) reprezentują ruch n krążków zgodnie z ruchem wskazówek zegara i przeciwnie do ruchu wskazówek zegara, wtedy możemy zapisać oba wzory:

 C(n) = ZA(n-1) n ZA(n-1) i A(n) = A(n-1) n C(n-1) n ZA(n-1). 

 Zatem C(1) = 1 i A(1) = 1 1, C(2) = 1 1 2 1 1 i A(2) = 1 1 2 1 2 1 1. 

Rozwiązanie dla Cyklicznego Hanoi ma kilka interesujących właściwości:

1) Wzorce ruchu podczas przenoszenia wieży dysków z kołka na inny kołek są symetryczne względem punktów środkowych.

2) Najmniejszy dysk to pierwszy i ostatni dysk do przeniesienia.

3) Grupy najmniejszych ruchów dysków przeplatają się z pojedynczymi ruchami innych dysków.

4) Liczba ruchów dysków określona przez C(n) i A(n) jest minimalna.

Z czterema kołkami i nie tylko

Chociaż wersja z trzema kołkami ma proste rozwiązanie rekurencyjne od dawna znane, optymalne rozwiązanie problemu Wieży Hanoi z czterema kołkami (zwane łamigłówką Reve'a) zostało zweryfikowane dopiero w 2014 roku przez Bouscha.

Jednak w przypadku czterech lub więcej kołków algorytm Frame-Stewart jest znany bez dowodu optymalności od 1941 roku.

Formalne wyprowadzenie dokładnej liczby minimalnych ruchów wymaganych do rozwiązania problemu za pomocą algorytmu Frame-Stewarta (i innych równoważnych metod) można znaleźć w poniższym artykule.

Aby zapoznać się z innymi wariantami problemu czterokołowej Wieży Hanoi, zobacz artykuł ankietowy Paula Stockmeyera.

Tak zwane konfiguracje gier Towers of Bucharest i Towers of Klagenfurt dają trójskładnikowe i pentarne kody Graya.

Algorytm ramy-Stewarta

Algorytm Frame-Stewarta opisano poniżej:

• Niech ${\ displaystyle n}$ będzie liczbą dysków.
• Niech $.$ liczbą kołków
• Zdefiniuj jako minimalną liczbę ruchów wymaganych do przeniesienia $.$

Algorytm można opisać rekurencyjnie:

1. $W$ przypadku niektórych przenieś górne ${\ Displaystyle T (k, r)}$$pojedynczy$$biorąc$ inny początkowe lub .
2. Bez naruszania kołka, który zawiera teraz górne $krążki$$r$ przenieś pozostałe do kołka docelowego, używając tylko pozostałych kołków, $displaystyle r-1$ wykonując ruchy ${\ Displaystyle T (nk, r-1)}$ .
3. $na$ górne $docelowy$ kołek ,

Cały proces trwa ${\ Displaystyle 2 T (k, r) + T (nk, r-1)}$ . Dlatego należy wybrać liczbę $minimalna .$ W przypadku 4-kołkowym optymalne równa się ${\ displaystyle k}$$prawo$$\ rceil + 1}$ , gdzie jest funkcją całkowitą . Na przykład w kursie UPenn CIS 194 dotyczącym Haskella pierwsza strona zadania zawiera listę optymalnych rozwiązań dla 15-krążkowej i 4-kołkowej obudowy jako 129 kroków, które uzyskuje się dla powyższej wartości k .

Zakłada się, że ten algorytm jest optymalny dla dowolnej liczby kołków; jego liczba ruchów wynosi 2 ^{Θ ( n 1/( r −2) )} (dla ustalonego r ).

Ogólne najkrótsze ścieżki i numer 466/885

Ciekawym uogólnieniem pierwotnego celu łamigłówki jest rozpoczęcie od określonej konfiguracji dysków, w której wszystkie dyski niekoniecznie znajdują się na tym samym kołku, i dotarcie w minimalnej liczbie ruchów do innej danej konfiguracji. Ogólnie rzecz biorąc, obliczenie najkrótszej sekwencji ruchów w celu rozwiązania tego problemu może być dość trudne. Rozwiązanie zostało zaproponowane przez Andreasa Hinza i opiera się na obserwacji, że w najkrótszej sekwencji ruchów największy dysk, który należy przesunąć (oczywiście można pominąć wszystkie największe dyski, które zajmą ten sam kołek zarówno w początkowym, jak i ostateczne konfiguracje) przesuną się dokładnie raz lub dokładnie dwa razy.

Matematyka związana z tym uogólnionym problemem staje się jeszcze bardziej interesująca, gdy weźmie się pod uwagę średnią liczbę ruchów w najkrótszej sekwencji ruchów między dwoma początkowymi i końcowymi konfiguracjami dysku, które są wybrane losowo. Hinz i Chan Tat-Hung niezależnie odkryli (patrz także ), że średnia liczba ruchów w n-dyskowej wieży jest określona następującym dokładnym wzorem:

${\ Displaystyle {\ Frac {466} {885}} \ cdot 2 ^ {n} - {\ Frac {1} {3}} - {\ Frac {3} {5}} \ cdot \ lewo ({\ frac {1}{3}}\right)^{n}+\left({\frac {12}{59}}+{\frac {18}{1003}}{\sqrt {17}}\right)\ left({\frac {5+{\sqrt {17}}}{18}}\right)^{n}+\left({\frac {12}{59}}-{\frac {18}{1003 }}{\sqrt {17}}\right)\left({\frac {5-{\sqrt {17}}}{18}}\right)^{n}.}$

${\ Displaystyle 466/885 \ cdot 2 ^ { n} -1/3 + o (1)}$ dużych n tylko pierwszy i drugi wyraz nie zbiegają się zera, więc otrzymujemy wyrażenie asymptotyczne : , jak ${\ Displaystyle n \ do \ infty}$ . Zatem intuicyjnie moglibyśmy zinterpretować ułamek ${\ Displaystyle 466/885 \ około 52,6 \%}$ jako reprezentujący stosunek pracy, którą trzeba wykonać, przechodząc z losowo wybranej konfiguracji do innej losowo wybranej konfiguracji, w stosunku do trudności z koniecznością przekroczenia „najtrudniejszej” ścieżki o długości ${\ Displaystyle 2 ^ {n} -1},$ co polega na przeniesieniu wszystkich dysków z jednego kołka na drugi. Alternatywne wyjaśnienie pojawienia się stałej 466/885, a także nowy i nieco ulepszony algorytm obliczania najkrótszej ścieżki podał Romik.

Magnetyczne Hanoi

Główny artykuł: Magnetyczna Wieża Hanoi

W Magnetic Tower of Hanoi każdy dysk ma dwie odrębne strony północną i południową (zwykle w kolorze „czerwonym” i „niebieskim”). Dyski nie mogą być umieszczane razem z podobnymi biegunami - magnesy w każdym dysku zapobiegają temu nielegalnemu ruchowi. Ponadto każdy dysk musi być odwracany podczas przesuwania.

Początkowa konfiguracja dwukolorowych wież Hanoi (n=4)

Dwukolorowe wieże Hanoi

Ta odmiana słynnej układanki Wieża Hanoi została zaoferowana uczniom klas 3-6 na 2ème Championnat de France des Jeux Mathématiques et Logiques, które odbyły się w lipcu 1988 roku.

Ostateczna konfiguracja dwukolorowych wież Hanoi (n=4)

Zasady układanki są zasadniczo takie same: dyski są przenoszone między kołkami pojedynczo. W żadnym momencie większy dysk nie może być umieszczony na mniejszym. Różnica polega na tym, że teraz dla każdego rozmiaru są dwa dyski: jeden czarny i jeden biały. Ponadto istnieją teraz dwie wieże dysków o naprzemiennych kolorach. Celem układanki jest sprawienie, aby wieże były monochromatyczne (ten sam kolor). Zakłada się, że największe dyski na dole wież zamieniają się miejscami.

Wieża Hanoy

Odmiana układanki została zaadaptowana jako gra w pasjansa z dziewięcioma kartami do gry pod nazwą Tower of Hanoy . Nie wiadomo, czy zmieniona pisownia pierwotnej nazwy jest celowa, czy przypadkowa.

Aplikacje

Topograficzny obraz 3D AFM wielowarstwowej nanocząstki palladu na płytce krzemowej, ze strukturą podobną do Wieży Hanoi.

Wieża Hanoi jest często wykorzystywana w psychologicznych badaniach nad rozwiązywaniem problemów . Istnieje również wariant tego zadania o nazwie Tower of London do neuropsychologicznej diagnozy i leczenia funkcji wykonawczych.

Zhang i Norman wykorzystali kilka izomorficznych (równoważnych) reprezentacji gry, aby zbadać wpływ efektu reprezentacji na projektowanie zadań. Wykazali wpływ na wydajność użytkownika, zmieniając sposób przedstawiania reguł gry, wykorzystując różnice w fizycznym projekcie komponentów gry. Ta wiedza wpłynęła na rozwój ram TURF do reprezentacji interakcji człowiek-komputer .

Wieża Hanoi jest również używana jako schemat rotacji kopii zapasowych podczas wykonywania kopii zapasowych danych komputerowych , w których zaangażowanych jest wiele taśm/nośników.

Jak wspomniano powyżej, Wieża Hanoi jest popularna do nauczania algorytmów rekurencyjnych dla początkujących studentów programowania. Obrazkowa wersja tej układanki jest zaprogramowana w emacs , dostępnym po wpisaniu Mx hanoi. Istnieje również przykładowy algorytm napisany w Prologu .

Wieża Hanoi jest również używana jako test przez neuropsychologów próbujących ocenić deficyty płata czołowego .

W 2010 roku naukowcy opublikowali wyniki eksperymentu, który wykazał, że gatunek mrówek Linepithema humile był w stanie z powodzeniem rozwiązać 3-dyskową wersję problemu Wieży Hanoi poprzez nieliniową dynamikę i sygnały feromonowe.

W 2014 roku naukowcy zsyntetyzowali wielowarstwowe nanocząstki palladu o strukturze przypominającej Wieżę Hanoi.

W kulturze popularnej

W opowiadaniu science fiction „Now Inhale”, autorstwa Erica Franka Russella , człowiek jest przetrzymywany jako więzień na planecie, gdzie lokalnym zwyczajem jest zmuszanie więźnia do grania w grę, dopóki nie zostanie wygrana lub przegrana przed egzekucją. Protagonista wie, że przybycie statku ratunkowego może zająć rok lub dłużej, więc decyduje się zagrać w Wieże Hanoi z 64 dyskami. Ta historia nawiązuje do legendy o mnichach buddyjskich grających w tę grę do końca świata.

W historii Doctor Who The Celestial Toymaker z 1966 roku , tytułowy złoczyńca zmusza Doktora do zagrania w grę Tower of Hanoi składającą się z dziesięciu elementów, składającą się z 1023 ruchów, zatytułowaną The Trilogic Game, w której elementy układają się w kształt piramidy po ułożeniu w stos.

W 2007 roku koncepcja problemu Towers Of Hanoi została wykorzystana w Professor Layton and the Diabolical Box w zagadkach 6, 83 i 84, ale dyski zostały zmienione na naleśniki. Zagadka opierała się na dylemacie, w którym szef kuchni restauracji musiał przenieść stos naleśników z jednego talerza na drugi, zachowując podstawowe zasady oryginalnej układanki (tj. większy naleśnik położyć na mniejszym, itp.)

W filmie Rise of the Planet of the Apes (2011) ta łamigłówka, zwana w filmie „Wieżą Lucasa”, jest używana jako test do badania inteligencji małp człekokształtnych.

Układanka regularnie pojawia się w grach przygodowych i łamigłówkach . Ponieważ jest łatwy do wdrożenia i łatwo rozpoznawalny, dobrze nadaje się do wykorzystania jako układanka w większej grze graficznej (np. Star Wars: Knights of the Old Republic i Mass Effect ). Niektóre implementacje wykorzystują proste dyski, ale inne ukrywają zagadkę w innej formie. Istnieje wersja zręcznościowa firmy Sega .

15-dyskowa wersja układanki pojawia się w grze Sunless Sea jako zamek do grobowca. Gracz ma możliwość kliknięcia każdego ruchu układanki, aby go rozwiązać, ale gra zauważa, że ​​​​ukończenie zajmie 32767 ruchów. Jeśli szczególnie oddany gracz kliknie do końca układanki, okazuje się, że ukończenie układanki nie odblokowuje drzwi.

W Yu-Gi-Oh! VRAINS , grupa hakerska o nazwie „Knight of Hanoi” tworzy strukturę o nazwie „Wieża Hanoi” w sieci wirtualnej rzeczywistości VRAINS o tej samej nazwie.

Zostało to po raz pierwszy użyte jako wyzwanie w Survivor Thailand w 2002 roku, ale zamiast pierścieni, elementy zostały wykonane tak, aby przypominały świątynię. Sook Jai rzucił wyzwanie pozbycia się Jeda, mimo że Shii-Ann doskonale wiedziała, jak rozwiązać zagadkę. Problem został przedstawiony jako część wyzwania z nagrodą w jednym z odcinków amerykańskiej wersji serialu telewizyjnego Survivor z 2011 roku . Obaj gracze ( Ozzy Lusth i Benjamin „Coach” Wade ) starali się zrozumieć, jak rozwiązać zagadkę i są wspomagani przez innych członków plemienia.

W Genshin Impact ta łamigłówka jest pokazana w zadaniu Faruzana „Mechanizm wczesnego uczenia się”, gdzie wspomina, że ​​postrzega ją jako mechanizm i używa jej do stworzenia prototypu zabawki dla dzieci. Nazywa to Pagoda .

Zobacz też

• Wzór ABACABA
• Schemat rotacji kopii zapasowych , aplikacja TOH
• Baguenaudier
• Rekurencja (informatyka)

Linki zewnętrzne

• Weisstein, Eric W. „Wieża Hanoi” . MathWorld .