Wykres Dycka
| Wykres Dycka | |
|---|---|
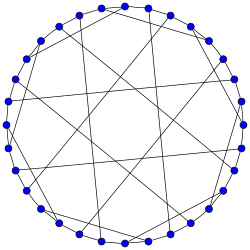 Wykres Dycka
| |
| Nazwany po | W Dyk |
| Wierzchołki | 32 |
| Krawędzie | 48 |
| Promień | 5 |
| Średnica | 5 |
| Obwód | 6 |
| Automorfizmy | 192 |
| Liczba chromatyczna | 2 |
| Indeks chromatyczny | 3 |
| Grubość książki | 3 |
| Numer kolejki | 2 |
| Nieruchomości |
Symetryczny sześcienny hamiltonian dwudzielny graf Cayleya |
| Tabela wykresów i parametrów | |
W matematycznej dziedzinie teorii grafów graf Dycka jest 3- regularnym grafem z 32 wierzchołkami i 48 krawędziami, nazwany na cześć Walthera von Dycka .
Jest hamiltonianem ze 120 różnymi cyklami hamiltonowskimi. Ma liczbę chromatyczną 2, indeks chromatyczny 3, promień 5, średnicę 5 i obwód 6. Jest to również graf spójny z 3 wierzchołkami i 3 krawędziami . Ma grubość książki 3 i numer kolejki 2.
Wykres Dycka jest grafem toroidalnym , a dualnym jego symetrycznym osadzeniem toroidalnym jest graf Shrikhande , silnie regularny graf zarówno symetryczny, jak i hamiltonowski.
Właściwości algebraiczne
Grupa automorfizmów grafu Dycka jest grupą rzędu 192. Działa przechodnio na wierzchołkach, krawędziach i łukach grafu. Dlatego wykres Dycka jest grafem symetrycznym . Ma automorfizmy, które przenoszą dowolny wierzchołek do dowolnego innego wierzchołka i dowolną krawędź do dowolnej innej krawędzi. Według spisu Fostera graf Dycka, oznaczony jako F32A, jest jedynym sześciennym grafem symetrycznym na 32 wierzchołkach.
Charakterystyczny wielomian wykresu Dycka jest równy .
Mapa Dycka
Wykres Dycka jest szkieletem symetrycznej teselacji powierzchni rodzaju trzy na dwanaście ośmiokątów, znanej jako mapa Dycka lub płytki Dycka . Graf dualny dla tego kafelkowania jest kompletnym grafem trójdzielnym K 4,4,4 .
Galeria
Alternatywny rysunek wykresu Dycka.
Liczba chromatyczna wykresu Dycka wynosi 2.
Indeks chromatyczny wykresu Dycka wynosi 3.
