Wykres Errery
| Wykres Errera | |
|---|---|
 Wykres Errery
| |
| Nazwany po | Alfreda Errery |
| Wierzchołki | 17 |
| Krawędzie | 45 |
| Promień | 3 |
| Średnica | 4 |
| Obwód | 3 |
| Automorfizmy | 20 ( D 10 ) |
| Liczba chromatyczna | 4 |
| Indeks chromatyczny | 6 |
| Nieruchomości |
Planarny hamiltonian |
| Tabela wykresów i parametrów | |
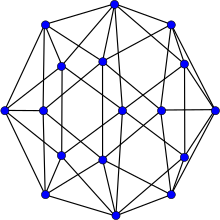
W matematycznej dziedzinie teorii grafów graf Errera to graf z 17 wierzchołkami i 45 krawędziami . Alfred Errera opublikował je w 1921 roku jako kontrprzykład dla błędnego dowodu twierdzenia o czterech kolorach przeprowadzonego przez Kempe ; został nazwany na cześć Errery przez Hutchinson & Wagon (1998) .
Nieruchomości
Graf Errery jest planarny i ma liczbę chromatyczną 4, indeks chromatyczny 6, promień 3, średnicę 4 i obwód 3. Wszystkie jego wierzchołki mają stopień 5 lub 6 i jest to graf złożony z 5 wierzchołków i 5 krawędzi wykres .
Wykres Errera nie jest grafem przechodnim wierzchołków , a jego pełna grupa automorfizmów jest izomorficzna z grupą dwuścienną rzędu 20, grupą symetrii dziesięciokąta , obejmującą zarówno obroty, jak i odbicia.
Wielomian charakterystyczny wykresu Errery to .
Zastosowanie do twierdzenia o czterech kolorach

Twierdzenie o czterech kolorach stwierdza, że wierzchołki każdego grafu planarnego można pokolorować czterema kolorami, tak że żadne dwa sąsiednie wierzchołki nie mają jednakowych kolorów. Błędny dowód został opublikowany w 1879 roku przez Alfreda Kempe , ale okazało się, że był błędny w 1890 roku . błędny. Kontrprzykłady do jego dowodu znaleziono w 1890 i 1896 roku ( wykres Poussina ), a później wykres Fritscha i wykres Soifera dostarczyły dwóch mniejszych kontrprzykładów. Jednak aż do pracy Errery te kontrprzykłady nie wykazały, że cały algorytm kolorowania zawodzi. Założyli raczej, że wszystkie wierzchołki wykresu oprócz jednego zostały już pokolorowane i wykazali, że metoda Kempe (która rzekomo zmodyfikowałaby kolorowanie, aby rozszerzyć je na całe wykresy) zawiodła w tych wstępnie pokolorowanych przypadkach. Z drugiej strony wykres Errera stanowi kontrprzykład dla całej metody Kempe. Kiedy ta metoda jest uruchamiana na grafie Errera, rozpoczynając od braku kolorowych wierzchołków, może nie znaleźć poprawnego kolorowania dla całego grafu. Dodatkowo, w przeciwieństwie do grafu Poussina, wszystkie wierzchołki w grafie Errera mają stopień piąty lub wyższy. Dlatego na tym grafie niemożliwe jest uniknięcie problematycznych przypadków metody Kempe poprzez wybór wierzchołków niższego stopnia.
Rysunek pokazuje przykład, w jaki sposób dowód Kempe może się nie powieść dla tego wykresu. Na rysunku sąsiedztwa między regionami tej mapy tworzą wykres Errera, częściowo czterokolorowy z niekolorowym obszarem zewnętrznym. Błędny dowód Kempe jest zgodny z ideą rozszerzenia kolorowań częściowych, takich jak ten, poprzez ponowne kolorowanie łańcuchów Kempe , połączonych podgrafów, które mają tylko dwa kolory. Każdy taki łańcuch można ponownie pokolorować, zachowując ważność kolorowania, zamieniając dwa kolory na wszystkich wierzchołkach łańcucha. Dowód Kempe ma różne przypadki w zależności od tego, czy następny wierzchołek, który ma być pokolorowany, ma trzech, czterech czy pięciu sąsiadów i od tego, w jaki sposób są pokolorowani. W pokazanym przypadku wierzchołek, który ma być pokolorowany w następnej kolejności, odpowiada zewnętrznemu regionowi mapy. Ten region nie może być bezpośrednio pokolorowany, ponieważ ma już sąsiadów we wszystkich czterech różnych kolorach. Niebiescy i żółci sąsiedzi są połączeni pojedynczym łańcuchem Kempe (pokazanym przez przerywane żółte linie na obrazie), co zapobiega zamianie, która powoduje, że oba są niebieskie lub oba żółte i uwalniają kolor. Podobnie niebieskie i zielone sąsiedztwo są połączone innym łańcuchem Kempe (przerywane zielone linie). W takim przypadku dowód Kempe próbowałby jednocześnie zamienić kolory na dwóch łańcuchach Kempe, lewym czerwono-żółtym łańcuchu i prawym czerwono-zielonym łańcuchu (przerywane czerwone linie). Niebiesko-zielony łańcuch blokuje lewy czerwono-żółty łańcuch przed dotarciem do prawej strony wykresu, a niebiesko-żółty łańcuch blokuje prawy czerwono-zielony łańcuch przed dotarciem do lewej, więc wydaje się, że równoczesna zamiana kolorów na tych dwa łańcuchy to bezpieczna operacja. Ponieważ jednak łańcuchy niebiesko-żółty i niebiesko-zielony przecinają się, a nie pozostają rozdzielone, na środku figury znajduje się obszar, w którym mogą się spotkać łańcuchy czerwono-żółty i czerwono-zielony. Kiedy te dwa łańcuchy spotykają się w środku, jednoczesna zamiana powoduje, że sąsiednie żółte i zielone wierzchołki w tym środkowym obszarze (takie jak wierzchołki reprezentowane przez górne żółte i zielone obszary na rysunku) stają się czerwone, powodując nieprawidłowe kolorowanie.
Zastosowania w chemii
Teoria grafów chemicznych dotyczy teoretycznej struktury grafów cząsteczek i innych skupisk atomów. Zarówno sam wykres Errera, jak i jego podwójny wykres są istotne w tym kontekście.
Atomy metali , takich jak złoto, mogą tworzyć klastry , w których centralny atom jest otoczony przez dwanaście innych atomów, na wzór dwudziestościanu . Inny, większy typ klastra można utworzyć przez połączenie dwóch z tych dwudziestościennych klastrów, tak że centralny atom każdego klastra staje się jednym z atomów granicznych dla drugiego klastra. Powstały klaster 19 atomów ma dwa atomy wewnętrzne (środki dwóch dwudziestościanów) z 17 atomami w powłoce zewnętrznej, zgodnie ze wzorem wykresu Errera.
Grafem dualnym grafu Errery jest fulleren z 30 wierzchołkami, oznaczony w literaturze chemicznej jako C 30 (D 5 h ) lub F 30 (D 5 h ) w celu wskazania jego symetrii i odróżnienia go od innych fullerenów o 30 wierzchołkach. Kształt ten odgrywa również kluczową rolę w konstruowaniu fullerenów o wyższych wymiarach.



