Wykres Tutte'a

Wszystkie wykresy
Wszystkie wykresy
Nazwany po	WT Tutte
Wierzchołki	46
Krawędzie	69
Promień	5
Średnica	8
Obwód	4
Automorfizmy	3 ( Z / 3 Z )
Liczba chromatyczna	3
Indeks chromatyczny	3
Nieruchomości	Sześcienny planarny wielościan
Tabela wykresów i parametrów

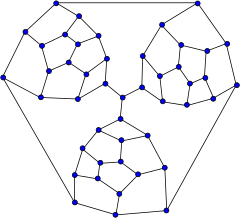
W matematycznej dziedzinie teorii grafów graf Tutte jest 3- regularnym grafem z 46 wierzchołkami i 69 krawędziami, nazwany na cześć WT Tutte . Ma liczbę chromatyczną 3, indeks chromatyczny 3, obwód 4 i średnicę 8.

Graf Tutte jest sześciennym grafem wielościennym , ale nie jest grafem hamiltonowskim . Dlatego jest to kontrprzykład dla hipotezy Taita , że ​​każdy 3-regularny wielościan ma cykl Hamiltona.

Opublikowany przez Tutte w 1946 roku, jest to pierwszy kontrprzykład skonstruowany dla tego przypuszczenia. Później znaleziono inne kontrprzykłady, w wielu przypadkach oparte na twierdzeniu Grinberga .

Budowa

Fragment Tutte.

Z małego płaskiego wykresu zwanego fragmentem Tutte, WT Tutte skonstruował wielościan niehamiltonowski, łącząc trzy takie fragmenty. „Obowiązkowe” krawędzie fragmentów, które muszą być częścią dowolnej ścieżki Hamiltona przez fragment, są połączone w centralnym wierzchołku; ponieważ każdy cykl może wykorzystywać tylko dwie z tych trzech krawędzi, nie może istnieć cykl Hamiltona.

Otrzymany graf jest 3-spójny i płaski , więc zgodnie z twierdzeniem Steinitza jest to wykres wielościanu. Ma 25 twarzy.

Można go zrealizować geometrycznie z czworościanu (którego ściany odpowiadają czterem dużym dziewięciobocznym ścianom na rysunku, z których trzy znajdują się między parami fragmentów, a czwarty tworzy zewnętrzną stronę) przez wielokrotne obcięcie trzech jego wierzchołków .

Właściwości algebraiczne

Grupa automorfizmów grafu Tutte to Z / 3 Z , grupa cykliczna rzędu 3.

Charakterystyczny wielomian wykresu Tutte'a to:

${\ Displaystyle (x-3) (x ^ {15} -22x ^ {13} + x ^ {12} + 184x ^ {11} -26x ^ ​​{10} - 731x^{9}+199x^{8}+1383x^{7}-576x^{6}-1061x^{5}+561x^{4}+233x^{3}-151x^{2}+4x+ 4)^{2}}$

${\ Displaystyle (x ^ {15} + 3x ^ {14} -16x ^ {13} -50x ^ {12} + 94x ^ {11} + 310x ^ {10} -257x ^ {9} -893x ^ {8 }+366x^{7}+1218x^{6}-347x^{5}-717x^{4}+236x^{3}+128x^{2}-56x+4).}$

Powiązane wykresy

Chociaż graf Tutte jest pierwszym odkrytym 3-regularnym grafem wielościennym niehamiltonowskim, nie jest to najmniejszy taki graf.

W 1965 Lederberg znalazł graf Barnette-Bosák-Lederberg na 38 wierzchołkach. W 1968 roku Grinberg skonstruował dodatkowe małe kontrprzykłady do hipotezy Taita - grafy Grinberga na 42, 44 i 46 wierzchołkach. W 1974 roku Faulkner i Younger opublikowali dwa kolejne grafy - grafy Faulknera-Youngera na 42 i 44 wierzchołkach.

Ostatecznie Holton i McKay wykazali, że istnieje dokładnie sześć niehamiltonowskich wielościanów o 38 wierzchołkach, które mają nietrywialne cięcia trójkrawędziowe. Powstają poprzez zastąpienie dwóch wierzchołków graniastosłupa pięciokątnego tym samym fragmentem, którego użyto w przykładzie Tutte.