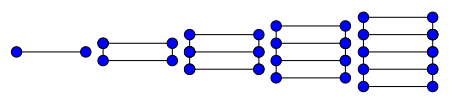
Wykres drabinkowy
| Wykres drabinkowy | |
|---|---|
 Wykres drabinkowy L 8 .
| |
| Wierzchołki | 2 przyp |
| Krawędzie | 3 n – 2 |
| Liczba chromatyczna | 2 |
| Indeks chromatyczny |
3 dla n > 2 2 dla n = 2 1 dla n = 1 |
| Nieruchomości |
Jednostkowa odległość hamiltonowska planarna dwudzielna |
| Notacja | L n |
| Tabela wykresów i parametrów | |
W matematycznej dziedzinie teorii grafów graf drabinkowy Ln nieskierowanym jest planarnym , grafem z 2 n wierzchołkami i 3 n – 2 krawędziami.
Wykres drabinkowy można otrzymać jako iloczyn kartezjański dwóch wykresów ścieżkowych , z których jeden ma tylko jedną krawędź: L n ,1 = P n × P 2 .
Nieruchomości
Z konstrukcji graf drabinkowy L n jest izomorficzny z grafem siatkowym G 2, n i wygląda jak drabina z n szczeblami. Jest hamiltonianem o obwodzie 4 (jeśli n>1 ) i indeksie chromatycznym 3 (jeśli n>2 ).
Liczba chromatyczna wykresu drabinkowego to 2, a jego wielomian chromatyczny to .
Liczba chromatyczna wykresu drabinkowego to 2.
Wykres szczebli drabiny
Czasami termin „wykres drabinkowy” jest używany w odniesieniu do wykresu szczebli drabinkowych n × P 2 , który jest połączeniem grafu n kopii wykresu ścieżkowego P 2 .
Okrągły wykres drabinkowy
Kołowy graf drabinkowy CL n można skonstruować, łącząc w prosty sposób cztery wierzchołki 2-stopniowe lub iloczyn kartezjański cyklu o długości n ≥ 3 i krawędzi. W symbolach CL n = do n × P 2 . Ma 2 n węzłów i 3 n krawędzi. Podobnie jak graf drabinkowy, jest spójny , planarny i hamiltonowski , ale jest dwudzielny wtedy i tylko wtedy, gdy n jest parzyste.
Kołowy wykres drabinkowy to wielościenny wykres graniastosłupa , dlatego częściej nazywany jest wykresem pryzmatycznym .
Kołowe wykresy drabinkowe:
 CL3 |
 CL4 |
 CL5 |
 CL6 |
 CL7 |
 CL8 |
Drabina Möbiusa
poprzeczne czterech wierzchołków 2-stopniowych tworzy graf sześcienny zwany drabiną Möbiusa.