Wykres przyjaźni

Wykres przyjaźni
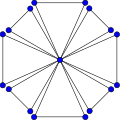Wykres przyjaźni F 8 .
Wierzchołki	2 n + 1
Krawędzie	3 przyp
Promień	1
Średnica	2
Obwód	3
Liczba chromatyczna	3
Indeks chromatyczny	2 przyp
Nieruchomości	Odległość jednostkowa Planarny eulerowski Czynnik krytyczny Lokalnie liniowy
Notacja	F przym
Tabela wykresów i parametrów

Wykresy przyjaźni F ₂ , F ₃ i F ₄ .

W matematycznej dziedzinie teorii grafów graf przyjaźni (lub holenderski Fn _wykres wiatraka lub n -wentylator ) jest planarnym , nieskierowanym grafem z 2 n + 1 wierzchołkami i 3 n krawędziami.

Graf przyjaźni F _n można zbudować łącząc n kopii wykresu cyklu C ₃ wspólnym wierzchołkiem, który staje się wierzchołkiem uniwersalnym dla grafu.

Z konstrukcji graf przyjaźni F _n jest izomorficzny z grafem wiatraka Wd(3, n ) . Jest to jednostka odległości o obwodzie 3, średnicy 2 i promieniu 1. Wykres F ₂ jest izomorficzny z wykresem motyla .

Twierdzenie o przyjaźni

Twierdzenie o przyjaźni Paula Erdősa , Alfréda Rényi i Very T. Sós ( 1966 ) stwierdza, że ​​grafy skończone, których każde dwa wierzchołki mają dokładnie jednego wspólnego sąsiada, są dokładnie grafami przyjaźni. Nieformalnie, jeśli grupa ludzi ma tę właściwość, że każda para ludzi ma dokładnie jednego wspólnego przyjaciela, to musi istnieć jedna osoba, która jest przyjacielem wszystkich pozostałych. Jednak w przypadku grafów nieskończonych może istnieć wiele różnych grafów o tej samej liczności, które mają tę właściwość.

Kombinatoryczny dowód twierdzenia o przyjaźni został podany przez Mertziosa i Ungera. Kolejny dowód dał Craig Huneke. Sformalizowany dowód w Metamath został zgłoszony przez Alexandra van der Vekensa w październiku 2018 roku na liście mailingowej Metamath.

Etykietowanie i kolorowanie

Wykres przyjaźni ma liczbę chromatyczną 3 i indeks chromatyczny 2 n . Jego wielomian chromatyczny można wywnioskować z wielomianu chromatycznego wykresu cyklu C ₃ i jest on równy

${\ Displaystyle (x-2) ^ {n} (x-1) ^ {n} x}$ .

Graf przyjaźni F _n jest pełen wdzięku na krawędziach wtedy i tylko wtedy, gdy n jest nieparzyste. Jest wdzięczny wtedy i tylko wtedy, gdy n ≡ 0 (mod 4) lub n ≡ 1 (mod 4) .

Każdy wykres przyjaźni jest czynnikiem krytycznym .

Ekstremalna teoria grafów

Zgodnie z teorią grafów ekstremalnych każdy $wykres$ z wystarczająco dużą liczbą krawędzi (w stosunku do liczby wierzchołków) musi zawierać jako podgraf. Dokładniej, dotyczy to $,$ jeśli liczba krawędzi wynosi

${\ Displaystyle \ lewo \ lfloor {\ Frac {n ^ {2}} {4}} \ prawo \ rfloor + f (k)}$

gdzie ${\ Displaystyle f (k)}$ jest ${\ Displaystyle k ^ {2} -k},$ jeśli ${\ Displaystyle k}$ jest nieparzyste i ${\ Displaystyle f (k ) )}$ jest równe ${\ Displaystyle k ^ {2} -3k/$$2$ . Te granice uogólniają twierdzenie Turána o liczbie krawędzi w grafie bez trójkątów i są najlepszymi możliwymi granicami tego problemu, ponieważ dla dowolnej mniejszej liczby krawędzi istnieją wykresy, które nie zawierają za k {\ $k}$ -wentylator.