Chiralny politop
W matematyce istnieją dwie konkurencyjne definicje chiralnego polytopu . Jednym z nich jest to, że jest to polytop , który jest chiralny (lub „enancjomorficzny”), co oznacza, że nie ma lustrzanej symetrii . Zgodnie z tą definicją polytop, który w ogóle nie ma symetrii, byłby przykładem chiralnego polytopu.
Inną, konkurencyjną definicją chiralnego polytopu jest to, że jest to polytop, który jest jak najbardziej symetryczny bez lustrzanej symetrii, sformalizowany pod względem działania grupy symetrii polytopu na jego flagach . Zgodnie z tą definicją, nawet wysoce symetryczne i enancjomorficzne polytopy, takie jak kostka snub, nie są chiralne. Wiele badań nad symetrycznymi, ale chiralnymi polytopami przeprowadzono w ramach abstrakcyjnych polytopów , ze względu na niedostatek przykładów geometrycznych.
Polytopy bez lustrzanej symetrii


|
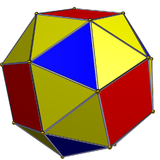
|
| Sześcian snub , wierzchołek przechodni, ale nie lustrzano-symetryczny. | |
Wiele polytopów nie ma lustrzanej symetrii iw tym sensie tworzą chiralne polytopy. Najprostszym przykładem jest trójkąt skaleniczny .
Możliwe jest, że polytopy mają wysoki stopień symetrii, ale brakuje im jeszcze symetrii lustrzanej; prostym przykładem jest disfenoid , gdy jego ściany nie są przystające do trójkąta równoramiennego ; innym przykładem jest kostka snub , która w tym sensie jest przechodnia przez wierzchołek i chiralna.
Symetryczne chiralne polytopy
Definicja
Bardziej techniczna definicja chiralnego polytopu to polytope, który ma dwie orbity flag w swojej grupie symetrii , z sąsiednimi flagami na różnych orbitach. Oznacza to, że musi być przechodnia wierzchołka , przechodnia krawędzi i przechodnia ściany , ponieważ każdy wierzchołek, krawędź lub ściana muszą być reprezentowane przez flagi na obu orbitach; nie może być jednak lustrzanie symetryczny, ponieważ każda symetria lustrzana polytopu wymieniałaby parę sąsiednich flag.
Dla celów tej definicji grupę symetrii polytopu można zdefiniować na dwa różne sposoby: może odnosić się do symetrii polytopu jako obiektu geometrycznego (w takim przypadku polytope nazywa się geometrycznie chiralnym) lub może odnoszą się do symetrii polytope jako struktury kombinatorycznej ( abstrakcyjna polytope ). Chiralność ma znaczenie dla każdego typu symetrii, ale dwie definicje klasyfikują różne politopy jako chiralne lub niechiralne.
W trzech wymiarach
W trzech wymiarach nie jest możliwe, aby geometrycznie chiralny polytop miał skończenie wiele skończonych ścian. Na przykład kostka snub jest przechodnia przez wierzchołki, ale jej flagi mają więcej niż dwie orbity i nie jest ani przechodnia krawędzi, ani przechodnia twarzy, więc nie jest wystarczająco symetryczna, aby spełnić formalną definicję chiralności. Wielościany kwaziregularne i ich liczby podwójne, takie jak ośmiościan sześcienny i dwunastościan rombowy , dostarczają innego interesującego typu sytuacji bliskich chybienia: mają dwie orbity flag, ale są lustrzanie symetryczne i nie każda sąsiednia para flag należy do różnych orbit. Jednak pomimo nieistnienia skończonych chiralnych trójwymiarowych wielościanów istnieją nieskończone trójwymiarowe chiralne wielościany skośne typu {4,6}, {6,4} i {6,6}.
Dalsza lektura
- Monson, Barry; Pisanski, Tomaž ; Schulte, Egon; Weiss , Asia Ivić ( 2007 ) _ _ _ _ _ _ MR 2310743 , S2CID 10203794 .
- Hubard, Izabela; Weiss, Asia Ivić (2005), „Samodualność chiralnych polytopów”, Journal of Combinatorial Theory , Seria A, 111 (1): 128–136, doi : 10.1016/j.jcta.2004.11.012 , MR 2144859 .
- Conder, Marston ; Hubard, Izabela; Pisanski, Tomaž (2008), „Konstrukcje dla chiralnych polytopów”, Journal of the London Mathematical Society , druga seria, 77 (1): 115–129, doi : 10.1112/jlms/jdm093 , MR 2389920 .
- Monson, Barry; Ivić Weiss, Asia (2008), „Wykresy Cayleya i symetryczne 4-politopy” , Ars Mathematica Contemporanea , 1 (2): 185–205, doi : 10.26493/1855-3974.79.919 , MR 2466196 .