Dwupromieniowy model odbicia od podłoża

Model odbicia dwóch promieni od podłoża to wielościeżkowy model propagacji radiowej , który przewiduje straty na ścieżce między anteną nadawczą a anteną odbiorczą, gdy znajdują się one w linii wzroku (LOS) . Ogólnie rzecz biorąc, każda z dwóch anten ma inną wysokość. Odebrany sygnał ma dwie składowe, składową LOS i składową odbiciową utworzoną głównie przez pojedynczą falę odbitą od podłoża.

Diagram odbicia 2 promieni od podłoża, w tym zmienne dla algorytmu propagacji odbicia 2 promieni od podłoża.

Wyprowadzenie matematyczne

Z rysunku otrzymaną składową linii celowania można zapisać jako

${\ Displaystyle r_ {los} (t) = Re \ lewo \ {{{ \frac {\lambda {\sqrt {G_{los}}}}{4\pi}}\times {\frac {s(t)e^{-j2\pi l/\lambda }}{l}}\ Prawidłowy\}}$

a składową odbitą od podłoża można zapisać jako

${\ Displaystyle r_ {gr} (t) = Re \ lewo \ {{\ Frac {\ lambda \ Gamma (\ theta) {\ sqrt {G_ {gr}}}} {4 \ pi}} \ razy {\ frac {s(t-\tau )e^{-j2\pi (x+x')/\lambda }}{x+x'}}\right\}}$

gdzie ${\ Displaystyle s (t)}$ jest transmitowanym sygnałem, $jest$ długością promienia bezpośredniego widzenia (LOS), $\ Displaystyle x + x '}$ to długość promienia odbitego od ziemi, to łączny zysk anteny wzdłuż ścieżki LOS, to $zysk$ sol $}}$ wzdłuż ścieżki odbitej od podłoża, $\ Displaystyle \ lambda} to$${\ Displaystyle \ lambda$$}$ transmisji ( , gdzie jest prędkością światła i ${\ Displaystyle f}$ to częstotliwość transmisji), $)}$$theta$ to współczynnik odbicia od podłoża, a to opóźnienia modelu równy ${\ Displaystyle (x + x'-l) / c}$ . Współczynnik odbicia od podłoża wynosi

${\ Displaystyle \ Gamma (\ teta) = {\ Frac {\ sin \ teta -X} {\ sin \ teta + X}}}$

gdzie ${\ Displaystyle X=X_ {h}}$ lub ${\ Displaystyle X=X_ {v}}$ w zależności od tego, czy sygnał jest odpowiednio spolaryzowany poziomo czy pionowo. ${\ displaystyle X}$ oblicza się w następujący sposób.

${\ Displaystyle X_ {h} = {\ sqrt {\ varepsilon _ {g} - {\ sałata} ^ {2}\theta}},\ X_{v}={\frac {\sqrt {\varepsilon _{g}-{\cos}^{2}\theta}}{\varepsilon _{g}}}= {\frac {X_{h}}{\varepsilon _{g}}}}$

Stała $kąt$ przenikalność gruntu (lub ogólnie rzecz biorąc, materiału, w którym sygnał jest odbijany), $między$ podłożem a odbity promień, jak pokazano na powyższym rysunku.

Z geometrii figury wynika:

${\ Displaystyle x + x '= {\ sqrt {(h_ {t} + h_ {r}) ^ {2} + d ^ {2}} }}$

I

${\ Displaystyle l = {\ sqrt {(h_ {t} -h_ {r}) ^ {2} + d ^ {2}}}}$ ,

Dlatego różnica długości ścieżek między nimi wynosi

${\ Displaystyle \ Delta d = x + x'-l = {\ sqrt {(h_{t}+h_{r})^{2}+d^{2}}}-{\sqrt {(h_{t}-h_{r})^{2}+d^{2} }}}$

a różnica faz między falami wynosi

${\ Displaystyle \ Delta \ phi = {\ Frac {2 \ pi \ Delta d} {\ lambda}}}$

Moc odbieranego sygnału wynosi

${\ Displaystyle P_ {r} = E \ {| r_ {los} (t) + r_ {gr} (t) | ^ {2} \}}$

gdzie $)$ średnią (w

Przybliżenie

Jeśli sygnał jest wąskim pasmem w stosunku do odwrotnego rozrzutu opóźnienia $)$ tak że $($ , równanie mocy można uprościć do

${\ Displaystyle {\ rozpocząć {wyrównane} P_ {r} = E \ {| s (t) | ^ {2} \} \ lewo ({\ Frac {\ lambda} {4 \ pi}} \ prawo) ^ { 2}\times \left|{\frac {{\sqrt {G_{los}}}\times e^{-j2\pi l/\lambda }}{l}}+\Gamma (\theta ){\sqrt {G_{gr}}}{\frac {e^{-j2\pi (x+x')/\lambda }}{x+x'}}\right|^{2}&=P_{t}\ left({\frac {\lambda }{4\pi}}\right)^{2}\times \left|{\frac {\sqrt {G_{los}}}{l}}+\Gamma (\theta ){\sqrt {G_{gr}}}{\frac {e^{-j\Delta \phi}}{x+x'}}\right|^{2}\end{wyrównane}}}$

gdzie ${\ Displaystyle P_ {t} = E \ {| s (t) | ^ {2} \}}$ to przesyłana moc.

Gdy odległość między antenami jest bardzo duża w stosunku $do$ wysokości anteny, możemy rozszerzyć $x'-l}$ ,

${\ Displaystyle {\ rozpocząć {wyrównane} \ Delta re =x+x'-l=d{\Bigg (}{\sqrt {{\frac {(h_{t}+h_{r})^{2}}{d^{2}}}+1}} -{\sqrt {{\frac {(h_{t}-h_{r})^{2}}{d^{2}}}+1}}{\Bigg )}\end{wyrównane}}}$

używając szeregu Taylora ${\ Displaystyle {\ sqrt {1 + x}}}$ :

${\ Displaystyle {\ sqrt {1 + x}} = 1 + \ textstyle {\ Frac {1} {2}} x - {\ Frac { 1}{8}}x^{2}+\kropki ,}$

i biorąc tylko pierwsze dwa wyrazy,

${\ Displaystyle x + x'-l \ około {\frac {d}{2}}\times \left({\frac {(h_{t}+h_{r})^{2}}{d^{2}}}-{\frac {( h_{t}-h_{r})^{2}}{d^{2}}}\right)={\frac {2h_{t}h_{r}}{d}}}$

Różnicę faz można następnie przybliżyć jako

${\ Displaystyle \ Delta \ phi \ około {\ Frac {4 \ pi h_ {t} h_ {r}} {\ lambda d}}}$

re ${\ Displaystyle d}$ jest duży, ${\ Displaystyle d \ gg (h_ {t} + h_ {r}$ }

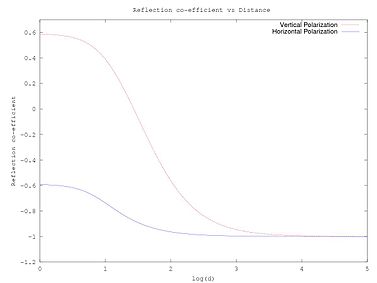
Współczynnik odbicia ma tendencję do -1 dla dużych d.

$\ Displaystyle {\ rozpocząć {wyrównane} d & \ około l \ około x + x ', \ \ Gamma (\theta )\około -1,\ G_{los}\około G_{gr}=G\end{wyrównane}}}$

i stąd

${\ Displaystyle P_ {r} \ około P_ {t} \ lewo ({\ Frac {\ lambda {\ sqrt {G}}} {4 \ pi d}} \ prawej) ^ {2} \ razy | 1- e^{-j\Delta \phi }|^{2}}$

${\ Displaystyle e ^ {- j \ Delta \ phi}}$ jot pomocą szeregu Taylora

${\ Displaystyle e ^ {x} = \ suma _ {n = 0} ^ {\ infty} {\ Frac {x ^ {n}} {n!} }=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots }$

i zachowując tylko dwa pierwsze terminy

${\ Displaystyle e ^ {-j \ Delta \ phi} \ około 1 + ({- j \ Delta \ phi}) + \cdots =1-j\Delta \phi }$

wynika, że

${\ Displaystyle {\ rozpocząć {wyrównane} P_ {r} i \ około P_ {t} \ lewo ({\ Frac {\ lambda {\ sqrt {G}}} {4 \ pi d}} \ prawej) ^ {2 }\times |1-(1-j\Delta \phi )|^{2}\\&=P_{t}\left({\frac {\lambda {\sqrt {G}}}{4\pi d }}\right)^{2}\times \Delta \phi ^{2}\\&=P_{t}\left({\frac {\lambda {\sqrt {G}}}{4\pi d} }\right)^{2}\times \left({\frac {4\pi h_{t}h_{r}}{\lambda d}}\right)^{2}\\&=P_{t} {\frac {Gh_{t}^{2}h_{r}^{2}}{d^{4}}}\end{wyrównane}}}$

aby

${\ Displaystyle P_ {r} \ około P_ {t} {\ Frac {Gh_ {t} ^ {2} h_ {r} ^ {2}} {d ^{4}}}}$

$jest$ dokładne w obszarze dalekiego pola, tj. gdy stopniach) lub równoważnie,

${\ Displaystyle d \ gg {\ Frac {4 \ pi h_ {t} h_ {r}} {\ lambda}}}$

a gdzie łączny zysk anteny jest iloczynem zysków anteny nadawczej i odbiorczej, ${\ Displaystyle G = G_ {t} G_ {r}}$ . Formułę tę po raz pierwszy uzyskał BA Vvedenskij.

Zauważ, że moc maleje wraz z odwrotnością czwartej potęgi odległości w polu dalekim, co można wytłumaczyć destrukcyjną kombinacją ścieżek bezpośrednich i odbitych, które mają mniej więcej taką samą wielkość i różnią się fazą o 180 stopni. nazywana jest „ $nadawcza$ izotropową mocą promieniowania” (EIRP), czyli mocą nadawania wymaganą do wytworzenia takiej samej odbieranej mocy, gdyby antena

W jednostkach logarytmicznych

W jednostkach logarytmicznych : ${\ Displaystyle P_ {r _ {\ tekst {dBm}}} = P_ { t_{\text{dBm}}}+10\log _{10}(Gh_{t}^{2}h_{r}^{2})-40\log _{10}(d)}$

Tłumienie ścieżki : ${\ Displaystyle PL \; = P_ {t_ {\ tekst {dBm }}}-P_{r_{\text{dBm}}}\;=40\log _{10}(d)-10\log _{10}(Gh_{t}^{2}h_{r}^ {2})}$

Charakterystyka mocy a odległości

Kiedy odległość między $.$ jest mniejsza niż wysokość anteny nadawczej, dwie fale są konstruktywnie dodawane, aby uzyskać większą moc Wraz ze wzrostem odległości fale te sumują się konstruktywnie i destrukcyjnie, tworząc regiony zanikania w górę i w dół. Gdy odległość wzrasta poza odległość krytyczną ${$ strefę Fresnela, moc spada proporcjonalnie do odwrotności czwartej potęgi d do $displaystyle d}$ . Przybliżenie odległości krytycznej można uzyskać, ustawiając Δφ na π jako odległość krytyczną do lokalnego maksimum.

Przedłużenie anteny o dużej wysokości

Powyższe przybliżenia są ważne pod warunkiem, że $co$ wielu scenariuszach, np. Gdy niewiele mniejsze w porównaniu z odległością lub gdy podłoża nie da się wymodelować jako płaszczyzny idealnej. $W$ takim przypadku nie można użyć i wymagana bardziej dokładna analiza,

Modelowanie propagacji dla platform wysokościowych , UAV , dronów itp.

Powyższe duże przedłużenie wysokości anteny można wykorzystać do modelowania kanału propagacji ziemia-powietrze, tak jak w przypadku powietrznego węzła komunikacyjnego, np. UAV, drona, platformy wysokościowej. Gdy $w$ powietrzu jest średnia do dużej, zależność już nie iw konsekwencji ${\ Displaystyle \ Gamma \ ok -1}$ też nie trzyma. Ma to ogromny wpływ na utratę ścieżki propagacji i typową głębokość zaniku oraz margines zaniku wymagany do niezawodnej komunikacji (niskie prawdopodobieństwo przestoju).

Jako przypadek logarytmicznego modelu utraty ścieżki na odległość

Standardowym wyrażeniem modelu tłumienia ścieżki logarytmicznej w [dB] jest

${\ Displaystyle PL \; = P_ {T_ {dBm}} -P_ {R_ {dBm} }\;=\;PL_{0}\;+\;10\nu \;\log _{10}{\frac {d}{d_{0}}}\;+\;X_{g},}$

gdzie jest zanikaniem na $jest$ (logarytm normalny), odległością odniesienia, przy której utrata ścieżki wynosi $}$$}}$$\ Displaystyle PL_ {0}$ , jest wykładnikiem utraty $ścieżki$ zazwyczaj ${\ Displaystyle \ nu = 2...4}$ . Model $szczególnie$ dobrze nadaje się do pomiarów, dzięki którym ν $\ displaystyle \ nu}$ są określane eksperymentalnie; $jest$ ze względu na wygodę pomiarów i dobrą widoczność. Ten model jest również wiodącym kandydatem do systemów 5G i 6G, a także jest używany do komunikacji w pomieszczeniach, patrz np. i odniesienia tam zawarte.

Tłumienie ścieżki [dB] modelu 2-promieniowego jest formalnie przypadkiem szczególnym z: ${\ displaystyle \ nu = 4}$ :

${\ Displaystyle PL \; = P_ {t_ {dBm}} -P_{r_{dBm}}\;=40\log_{10}(d)-10\log_{10}(Gh_{t}^{2}h_{r}^{2})}$

gdzie ${\ Displaystyle d_ {0} = 1}$ , ${\ Displaystyle X_ {g} = 0}$ i

${\ Displaystyle PL_ {0} = -10 \ log _ {10} (Gh_ {t} ^ {2} h_ {r} ^ {2} )}$ ,

co jest ważne dla dalekiego pola, ${\ Displaystyle d> d_ {c} = 4 \ pi h_ {r} h_ {t}/\ lambda}$ = odległość krytyczna.

W przypadku modelu wielospadowego

Model 2-promieniowego odbitego od podłoża można traktować jako przypadek modelu wielokierunkowego z punktem załamania w odległości krytycznej o nachyleniu 20 dB/dekadę przed odległością krytyczną i nachyleniu 40 dB/dekadę po odległości krytycznej. Korzystając z powyższego modelu wolnej przestrzeni i modelu dwupromieniowego, utratę ścieżki propagacji można wyrazić jako

${\ Displaystyle L = \ max \ {G, L_ {min}, L_ {FS}, L_ {2-ray} \ }}$

gdzie ${\ Displaystyle L_ {FS} = (4 \ pi d / \ lambda) ^ {2}}$ i ${\ Displaystyle L_ {2-promień} = d ^ {4}/(h_ {t} h_ {r}) ^ {2}}$ to straty w wolnej przestrzeni i na ścieżce 2 promieni; ${\ Displaystyle L_ {min.}}$ to minimalna utrata ścieżki (przy najmniejszej odległości), zwykle w praktyce; ${\ Displaystyle L_ {min} \ około 20}$ dB lub więcej. Zauważ, że $geq G},$$\$ a także wynikają prawa zachowania energii (ponieważ moc Rx nie może przekroczyć mocy Tx), tak ${\ Displaystyle L_ {FS} = (4 \ pi d / \ lambda) ^ {2}}$ i ${r}) ^ {2}}$${\ Displaystyle L_ {2-ray} = d ^ {4} / (h_ {t}$$mały$ rozkłada się, gdy jest wystarczająco . Należy o tym pamiętać, stosując te przybliżenia na małych odległościach (ignorowanie tego ograniczenia czasami daje absurdalne wyniki).

Zobacz też

• Model propagacji radiowej
• Utrata ścieżki w wolnej przestrzeni
• Równanie transmisji Friisa
• ITU-R P.525
• Budżet łącza
• Śledzenie promieni (fizyka)
• Odbicie (fizyka)
• Lustrzane odbicie
• Model sześciu promieni
• Model dziesięciu promieni

Dalsza lektura

• S. Salous, Pomiar propagacji radiowej i modelowanie kanałów, Wiley, 2013.
• JS Seybold, Wprowadzenie do propagacji RF, Wiley, 2005.
• K. Siwiak, Propagacja fal radiowych i anteny do komunikacji osobistej, Artech House, 1998.
• MP Doluhanov, Propagacja fal radiowych, Moskwa: Sviaz, 1972.
• VV Nikolskij, TI Nikolskaja, Elektrodynamika i propagacja fal radiowych, Moskwa: Nauka, 1989.
• 3GPP TR 38.901, Badanie modelu kanału dla częstotliwości od 0,5 do 100 GHz (wydanie 16), Sophia Antipolis, Francja, 2019 [2]
• Zalecenie ITU-R P.1238-8: Dane propagacyjne i metody predykcyjne do planowania wewnętrznych systemów radiokomunikacyjnych i lokalnych sieci radiowych w zakresie częstotliwości od 300 MHz do 100 GHz [3]
• S. Loyka, ELG4179: Podstawy komunikacji bezprzewodowej, notatki z wykładów (wykład 2-4), University of Ottawa, Kanada, 2021 [4]