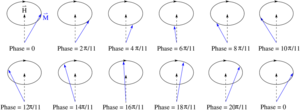
Fala wirowania

Fala spinowa to rozchodzące się zaburzenie uporządkowania materiału magnetycznego. Te nisko położone zbiorowe wzbudzenia występują w sieciach magnetycznych o ciągłej symetrii . Z równoważnego punktu widzenia kwazicząstek fale spinowe są znane jako magnony , które są modami bozonowymi sieci spinowej, które odpowiadają z grubsza wzbudzeniom fononowym sieci jądrowej. Wraz ze wzrostem temperatury wzbudzenie termiczne fal spinowych zmniejsza spontaniczne namagnesowanie ferromagnesu . Energie fal spinowych wynoszą zwykle tylko $μeV$ , zgodnie z typowymi punktami Curie w temperaturze pokojowej i niższej.

Teoria

Ilustracja precesji fali spinowej o długości fali, która jest jedenaście razy większa od stałej sieci wokół przyłożonego pola magnetycznego.

Rzut namagnesowania tej samej fali spinowej wzdłuż kierunku łańcucha w funkcji odległości wzdłuż łańcucha spinowego.

Najprostszym sposobem zrozumienia fal spinowych jest rozważenie hamiltonianu dla ferromagnesu Heisenberga: H. $\ displaystyle {\ mathcal {H}}}$

{\ Displaystyle {\ mathcal {H}} = - {\ Frac {1} {2}} J \ suma _{i,j}\mathbf {S} _{i}\cdot \mathbf {S} _{j}-g\mu _{\rm {B}}\sum _{i}\mathbf {H} \ cdot \mathbf {S} _{i}}

gdzie $J$ to energia wymiany , operatory $S$ reprezentują spiny w punktach sieci Bravais , $g$ to współczynnik Landé $g$ , $μ B$ to magneton Bohra , a $H$ to pole wewnętrzne, które obejmuje pole zewnętrzne oraz dowolne pole „molekularne”. Zauważ, że w klasycznym przypadku continuum iw wymiarach $1 + 1 równanie$ ferromagnesu Heisenberga ma postać

{\ Displaystyle \ mathbf {S} _ {t} = \ mathbf {S} \ razy \ mathbf {S} _ {xx}.}

W wymiarach $1 + 1, 2 + 1$ i $3 + 1$ to równanie dopuszcza kilka całkowalnych i niecałkowalnych rozszerzeń, takich jak równanie Landaua-Lifshitza , równanie Ishimoriego i tak dalej. Dla ferromagnesu $J > 0$ i stanu podstawowego hamiltonianu ${\ Displaystyle | 0 \ rangle}$ to taki, w którym wszystkie spiny są wyrównane równolegle do pola $H$ . To ${\ Displaystyle | 0 \ rangle}$ jest stanem własnym ${\ displaystyle {\ mathcal {H}}}$ można zweryfikować, przepisując go pod względem operatorów podnoszących i obniżających wirowanie podanych przez:

{\ Displaystyle S ^ {\ pm} = S ^ {x} \ pm iS ^ {y}}

w wyniku

{\ Displaystyle {\ mathcal {H}} = - {\ Frac {1} {2}} J \ suma _ {i, j} S_ {i} ^ {z} S_ {j} ^ {z} -g \ mu _{\rm {B}}H\suma _{i}S_{i}^{z}-{\frac {1}{4}}J\suma _{i,j}(S_{i}^ {+}S_{j}^{-}+S_{i}^{-}S_{j}^{+})}

gdzie $z$ przyjęto kierunek pola magnetycznego. Operator obniżający spin $S -$ anihiluje stan z minimalnym rzutem spinu wzdłuż osi $z$ , podczas gdy operator podnoszący spin $S +$ anihiluje stan podstawowy z maksymalnym rzutem spinu wzdłuż osi $z$ . Od

{\ Displaystyle S_ {i} ^ {z} | 0 \ rangle = s | 0 \ rangle}

dla maksymalnie wyrównanego stanu znajdujemy

{\ Displaystyle {\ mathcal {H}} | 0 \ rangle = \ lewo (-Js ^ {2} - g \ mu _ {\ rm {B}} Hs \ prawej) N | 0 \ rangle}

gdzie N to całkowita liczba miejsc sieci Bravais. Twierdzenie, że stan podstawowy jest stanem własnym hamiltonianu, zostało potwierdzone.

Można by się domyślić, że pierwszy stan wzbudzony hamiltonianu ma jeden losowo wybrany spin w pozycji $i$ obrócony tak, że

{\ Displaystyle S_ {i} ^ {z} | 1 \ rangle = (s-1) | 1 \ rangle,}

ale w rzeczywistości ten układ spinów nie jest stanem własnym. Powodem jest to, że taki stan jest przekształcany przez operatory podnoszenia i opuszczania spinu. Operator zwiększy projekcję $z$ wirowania w pozycji $i z powrotem$ $}$ orientacji niskoenergetycznej, ale operator $^{-}}$ ${\ displaystyle S_ {i} ^ {$ obniży projekcję $z$ wirowania w pozycji $j$ . Połączony efekt dwóch operatorów polega zatem na propagacji obróconego spinu do nowej pozycji, co jest wskazówką, że prawidłowym stanem własnym jest fala spinowa , a mianowicie superpozycja stanów z jednym zredukowanym spinem. Kara za wymianę energii związana ze zmianą orientacji jednego spinu jest zmniejszana przez rozłożenie zakłócenia na dużej długości fali. Stopień dezorientacji dowolnych dwóch sąsiednich spinów jest w ten sposób zminimalizowany. Z tego wyjaśnienia można zrozumieć, dlaczego modelu Isinga ma dyskretną symetrię nie ma fal spinowych: pojęcie rozprzestrzeniania się zaburzenia w sieci spinowej na dużej długości fali nie ma sensu, gdy spiny mają tylko dwie możliwe orientacje. Istnienie wzbudzeń niskoenergetycznych jest związane z faktem, że przy braku pola zewnętrznego układ spinowy ma nieskończoną liczbę zdegenerowanych stanów podstawowych z nieskończenie różnymi orientacjami spinu. Istnienie tych stanów podstawowych widać z faktu, że stan ${\ Displaystyle | 0 \ rangle}$ nie ma pełnej symetrii obrotowej hamiltonianu ${\ Displaystyle {\ mathcal {H}}}$ , zjawisko zwane spontanicznym łamaniem symetrii .

Namagnesowanie

Wzbudzenie w środku siatki spinów rozchodzi się poprzez wymianę momentu obrotowego (a tym samym momentu pędu) z sąsiadami.

W tym modelu namagnesowanie

{\ Displaystyle M = {\ Frac {N \ mu _ {\ rm {B}} gs} {V}}}

gdzie $V$ jest objętością. Rozchodzenie się fal spinowych opisuje równanie ruchu Landaua-Lifshitza:

{\ Displaystyle {\ Frac {d \ mathbf {M}} {dt}} = - \ gamma \ mathbf {M} \ razy \mathbf {H} -{\frac {\lambda \mathbf {M} \times (\mathbf {M} \times \mathbf {H} )}{M^{2}}}}

gdzie $γ$ to współczynnik żyromagnetyczny, a $λ$ to stała tłumienia. Iloczyny krzyżowe w tym nieprzyzwoicie wyglądającym równaniu pokazują, że rozchodzeniem się fal spinowych rządzą momenty generowane przez pola wewnętrzne i zewnętrzne. (Równoważną postacią jest równanie Landaua-Lifshitza-Gilberta , które zastępuje ostatni wyraz bardziej „prosto wyglądającym” równoważnikiem).

Pierwszy człon po prawej stronie równania opisuje precesję namagnesowania pod wpływem przyłożonego pola, podczas gdy wspomniany wyżej człon końcowy opisuje, jak wektor magnetyzacji „skręca się” w kierunku pola w miarę upływu czasu. W metalach siły tłumienia opisane stałą $λ$ są w wielu przypadkach zdominowane przez prądy wirowe.

Jedna ważna różnica między fononami i magnonami polega na ich relacjach dyspersji . Zależność dyspersji dla fononów jest liniowa pierwszego rzędu w wektorze falowym $k$ , a mianowicie $ώ = ck$ , gdzie $ω$ to częstotliwość, a $c$ to prędkość dźwięku. Magnony mają paraboliczną zależność dyspersji: $ώ = Ak 2$ , gdzie parametr $A$ reprezentuje „ sztywność wirowania ”. k $2_$ forma jest trzecim członem rozwinięcia Taylora członu cosinusowego w wyrażeniu na energię pochodzącym z iloczynu skalarnego $S i \cdot S j$ . Podstawową przyczyną różnicy w relacji dyspersyjnej jest to, że parametr porządku (magnesowanie) stanu podstawowego w ferromagnesach narusza symetrię odwrócenia czasu . Dwa sąsiednie spiny w bryle o stałej sieci $a$ , które uczestniczą w modzie z wektorem falowym $k$ , mają między sobą kąt równy $ka$ .

Obserwacja eksperymentalna

Fale spinowe obserwuje się za pomocą czterech metod eksperymentalnych: nieelastycznego rozpraszania neutronów , nieelastycznego rozpraszania światła ( rozpraszanie Brillouina , rozpraszanie Ramana i nieelastyczne rozpraszanie promieniowania rentgenowskiego ), nieelastycznego rozpraszania elektronów ( spektroskopia strat energii elektronów z rozdzielczością spinową ) i rezonans fali spinowej ( ferromagnetyczne rezonans ). W pierwszej metodzie mierzy się utratę energii wiązki neutronów, które wzbudzają magnon, zwykle jako funkcję wektora rozpraszania (lub równoważnie przeniesienia pędu), temperatury i zewnętrznego pola magnetycznego. Pomiary nieelastycznego rozpraszania neutronów mogą określić krzywą dyspersji dla magnonów, tak samo jak dla fononów . Ważne urządzenia do rozpraszania neutronów nieelastycznych znajdują się w źródle neutronów ISIS w Oxfordshire w Wielkiej Brytanii, Institut Laue-Langevin w Grenoble we Francji, High Flux Isotope Reactor w Oak Ridge National Laboratory w Tennessee w USA oraz w National Institute of Standards and Technology w Maryland w USA. Rozpraszanie Brillouina w podobny sposób mierzy utratę energii fotonów (zwykle o dogodnej widzialnej długości fali) odbijanych lub transmitowanych przez materiał magnetyczny. Spektroskopia Brillouina jest podobna do szerzej znanego rozpraszania Ramana , ale bada niższą energię i ma lepszą rozdzielczość energii, aby móc wykryć energię meV magnonów. Zamiast tego rezonans ferromagnetyczny (lub antyferromagnetyczny) mierzy absorpcję mikrofal , padające na materiał magnetyczny, przez fale spinowe, zwykle jako funkcja kąta, temperatury i przyłożonego pola. Rezonans ferromagnetyczny jest wygodną laboratoryjną metodą określania wpływu anizotropii magnetokrystalicznej na dyspersję fal spinowych. Jedna grupa z Instytutu Fizyki Mikrostruktur im. Maxa Plancka w Halle w Niemczech udowodniła, że za pomocą spektroskopii strat energii elektronów spolaryzowanych spinowo (SPEELS), bardzo wysokoenergetyczne magnony powierzchniowe mogą być wzbudzane. Ta technika pozwala badać dyspersję magnonów w ultracienkich warstwach ferromagnetycznych. Pierwszy eksperyment przeprowadzono dla 5 ml filmu Fe. Z rozdzielczością pędu zbadano dyspersję magnon odpowiednio dla filmu 8 ML fcc Co na Cu (001) i 8 ML hcp Co na W (110). Maksymalna energia magnona na granicy powierzchniowej strefy Brillouina wyniosła 240 meV.

Praktyczne znaczenie

Kiedy urządzenia magnetoelektroniczne działają z wysokimi częstotliwościami, generowanie fal spinowych może być ważnym mechanizmem utraty energii. Generowanie fal spinowych ogranicza szerokości linii, a tym samym współczynniki jakości Q elementów ferrytowych stosowanych w urządzeniach mikrofalowych . Odwrotność najniższej częstotliwości charakterystycznych fal spinowych materiału magnetycznego daje skalę czasową przełączania urządzenia opartego na tym materiale.

Zobacz też

Anderson, Philip W. (1997). Pojęcia w ciałach stałych: wykłady z teorii ciał stałych (red. Repr.). Singapur: świat naukowy. ISBN 981-02-3231-4 .
Anderson, Philip W. (1997). Podstawowe pojęcia fizyki materii skondensowanej . Cambridge, Massachusetts: Perseus Publishing. ISBN 0-201-32830-5 .
Ashcroft, Neil W.; Mermin, N. David (1977). Fizyka ciała stałego (27. repr. red.). Nowy Jork: Holt, Rinehart i Winston. ISBN 0-03-083993-9 .
Chikazumi, Soshin (1997). Fizyka ferromagnetyzmu (wyd. 2). Oksford: Oxford University Press. ISBN 0191569852 .

Linki zewnętrzne

Spin Waves Biennial International Symposium w celu omówienia najnowszych postępów w podstawowych badaniach właściwości dynamicznych różnych magnetycznie uporządkowanych materiałów.
Lista laboratoriów wykonujących pomiary rozpraszania Brillouina.