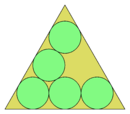
Koło upakowania w trójkącie równobocznym

Upakowanie okręgów w trójkącie równobocznym to problem upakowania w matematyce dyskretnej , w którym celem jest upakowanie $n$ jednostkowych okręgów w najmniejszy możliwy trójkąt równoboczny . Znane są rozwiązania optymalne dla $n <13$ i dowolnej trójkątnej liczby kół, a przypuszczenia są dostępne dla $n <28$ .

Przypuszczenie Paula Erdősa i Normana Olera stwierdza, że jeśli $n$ jest liczbą trójkątną, to optymalne upakowania $n - 1$ i $n$ okręgów mają tę samą długość boku: to znaczy, zgodnie z przypuszczeniem, optymalne upakowanie dla $n - 1$ koła można znaleźć, usuwając dowolne pojedyncze koło z optymalnego sześciokątnego upakowania $n$ kół. Obecnie wiadomo, że to przypuszczenie jest prawdziwe dla $n \leq 15$ .

Rozwiązania minimalne dla długości boku trójkąta:

Liczba kręgów	Jest trójkątny	Długość	Obszar
1	PRAWDA	${\ Displaystyle 2 {\ sqrt {3}}}$ = 3,464 ...	5.196...
2	FAŁSZ	${\ Displaystyle 2 + 2 {\ sqrt {3}}}$ = 5,464...	12.928...
3	PRAWDA	${\ Displaystyle 2 + 2 {\ sqrt {3}}}$ = 5,464...	12.928...
4	FAŁSZ	${\ Displaystyle 4 {\ sqrt {3}}}$ = 6,928...	20.784...
5	FAŁSZ	${\ Displaystyle 4 + 2 {\ sqrt {3}}}$ = 7,464...	24.124...
6	PRAWDA	${\ Displaystyle 4 + 2 {\ sqrt {3}}}$ = 7,464...	24.124...
7	FAŁSZ	${\ Displaystyle 2 + 4 {\ sqrt {3}}}$ = 8,928...	34.516...
8	FAŁSZ	${\ Displaystyle 2 + 2 {\ sqrt {3}} + {\ dfrac {2} {3}} {\ sqrt {33}}}$ = 9,293...	37.401...
9	FAŁSZ	${\ Displaystyle 6 + 2 {\ sqrt {3}}}$ = 9,464...	38.784...
10	PRAWDA	${\ Displaystyle 6 + 2 {\ sqrt {3}}}$ = 9,464...	38.784...
11	FAŁSZ	${\ Displaystyle 4 + 2 {\ sqrt {3}} + {\ dfrac {4} {3}} {\ sqrt {6}}}$ = 10,730...	49.854...
12	FAŁSZ	${\ Displaystyle 4 + 4 {\ sqrt {3}}}$ = 10,928...	51.712...
13	FAŁSZ	${\ Displaystyle 4 + {\ dfrac {10} {3}} {\ sqrt {3}} + {\ dfrac {2} {3}} {\ sqrt {6}}}$ = 11,406...	56.338...
14	FAŁSZ	${\ Displaystyle 8 + 2 {\ sqrt {3}}}$ = 11,464...	56.908...
15	PRAWDA	${\ Displaystyle 8 + 2 {\ sqrt {3}}}$ = 11,464...	56.908...

Ściśle powiązanym problemem jest pokrycie trójkąta równobocznego ustaloną liczbą równych okręgów o jak najmniejszym promieniu.

Zobacz też

Koło upakowane w trójkącie prostokątnym równoramiennym
Koła Malfattiego , konstrukcja dająca optymalne rozwiązanie dla trzech kół w trójkącie równobocznym

^ ^{ab Melissen, Hans (1993),}^„ Najgęstsze upakowania przystających kręgów w trójkącie równobocznym”, The American Mathematical Monthly , 100 (10): 916–925, doi : 10.2307/2324212 , JSTOR 2324212 , MR 1252928 .
Bibliografia _ Schuur, PC (1995), „Pakowanie 16, 17 lub 18 okręgów w trójkącie równobocznym” , Discrete Mathematics , 145 (1–3): 333–342, doi : 10,1016 / 0012-365X (95) 90139-C , MR 1356610 .
Bibliografia _ _ Lubachevsky, BD (1995), „Gęste upakowania równych dysków w trójkącie równobocznym: od 22 do 34 i dalej” , Electronic Journal of Combinatorics , 2 : Artykuł 1, ok. 39 s. (elektroniczny), MR 1309122 .
Bibliografia _ _ _ _ _ _ _ _ _ _ _ _
Bibliografia _ _ _ _ _ _ S0012-365X(96)00201-4 , MR 1439300 .
Bibliografia _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 45127090 .

[Melissen-1] {ab Melissen, Hans (1993),}^„ Najgęstsze upakowania przystających kręgów w trójkącie równobocznym”, The American Mathematical Monthly , 100 (10): 916–925, doi : 10.2307/2324212 , JSTOR 2324212 , MR 1252928 .

[2] Bibliografia _ Schuur, PC (1995), „Pakowanie 16, 17 lub 18 okręgów w trójkącie równobocznym” , Discrete Mathematics , 145 (1–3): 333–342, doi : 10,1016 / 0012-365X (95) 90139-C , MR 1356610 .

[3] Bibliografia _ _ Lubachevsky, BD (1995), „Gęste upakowania równych dysków w trójkącie równobocznym: od 22 do 34 i dalej” , Electronic Journal of Combinatorics , 2 : Artykuł 1, ok. 39 s. (elektroniczny), MR 1309122 .

[4] Bibliografia _ _ _ _ _ _ _ _ _ _ _ _

[5] Bibliografia _ _ _ _ _ _ S0012-365X(96)00201-4 , MR 1439300 .

[6] Bibliografia _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 45127090 .

Problemy z pakowaniem
Pakowanie abstrakcyjne	Kosz Ustawić
Pakowanie w kółko	W kole / trójkącie równobocznym / trójkącie prostokątnym równoramiennym / kwadracie uszczelka apollińska Twierdzenie o pakowaniu okręgu Problem Tammesa (na kuli)
Pakowanie kulek	apolliński Skończone W kuli w sześcianie W cylindrze Zamknięte opakowanie Całowanie numeru Pakowanie sferyczne (Hamming) związane
Inne opakowanie 2-D	Kwadratowe opakowanie w kwadracie
Inne opakowanie 3D	Czworościan Elipsoida
Puzzle	Conway Slothouber-Graatsma