Kwadratowe opakowanie w kwadracie

Nierozwiązany problem z matematyki :

Jaka jest asymptotyczna stopa wzrostu zmarnowanej przestrzeni dla kwadratowego upakowania w kwadracie półcałkowitym?

(więcej nierozwiązanych problemów z matematyki)

Kwadratowe upakowanie w kwadracie to problem z pakowaniem , w którym celem jest określenie, ile kwadratów o boku pierwszym ( kwadraty jednostkowe ) można upakować w kwadrat o boku za $\ displaystyle a}$ . Jeśli jest $,$ całkowitą odpowiedzią jest , ${\$ dokładna, a nawet asymptotyczna ilość zmarnowanego miejsca na $displaystyle a}$ niecałkowitą to za pytanie otwarte.

Mała liczba kwadratów

5 jednostkowych kwadratów w kwadracie o długości boku ${\ Displaystyle 2 + 1 / {\ sqrt {2}} \ około 2,707}$

10 jednostkowych kwadratów w kwadracie o długości boku ${\ Displaystyle 3 + 1 / {\ sqrt {2}} \ około 3,707}$

11 kwadratów jednostkowych w kwadracie o długości boku ${\ Displaystyle a \ około 3,877084}$

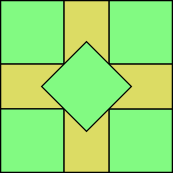
Najmniejsza wartość $n$ która pozwala na upakowanie kwadratów jednostkowych, jest znana, gdy jest ${\ displaystyle {\ sqrt$ idealny kwadrat (w takim przypadku jest to n ${}$$n}}}$$\ displaystyle n$ ), jak również dla ${\ displaystyle n = {}}$ 2, 3, 5, 6, 7, 8, 10, 13, 14, 15, 24, 34, 35, 46, 47, i 48. W przypadku większości z tych liczb (z wyjątkiem tylko 5 i 10) upakowanie jest naturalne z kwadratami wyrównanymi do osi i jest ${\ displaystyle a}$${\ Displaystyle \ lceil {\ sqrt {n}} \ \ rceil}$ , gdzie ${\ Displaystyle \ lceil \, \ \ rceil}$ jest funkcją sufitu (zaokrąglającą w górę). Rysunek przedstawia optymalne upakowanie dla 5 i 10 kwadratów, czyli dwie najmniejsze liczby kwadratów, dla których optymalne upakowanie obejmuje nachylone kwadraty.

Najmniejszy nierozwiązany przypadek obejmuje upakowanie 11 kwadratów jednostkowych w większy kwadrat. 11 jednostkowych kwadratów ${\ Displaystyle \ textstyle 2 + 2 {\ sqrt {4/5}} \ około 3,789}$ upakować w kwadracie o boku mniejszym niż . Z kolei najciaśniejsze znane upakowanie 11 kwadratów znajduje się wewnątrz kwadratu o długości boku około 3,877084, nieco poprawiając podobne upakowanie znalezione wcześniej przez Waltera Trumpa .

Wyniki asymptotyczne

$W przypadku większych$ długości boku $pozostaje$ liczba jednostkowych kwadratów, które mogą spakować nieznana. Zawsze jest możliwe spakowanie $osi kwadratów$ jednostkowych, ale może około ${\ Displaystyle 2a (a-\ lfloor a \ rfloor)}$ , odkryte i zmarnowane. Zamiast tego Paul Erdős i Ronald Graham wykazali $, że$ można znacznie zmniejszyć do napisane w małej notacji o ). Później Graham i Fan Chung jeszcze bardziej zredukowali zmarnowaną przestrzeń do ${\ Displaystyle O (a ^ {3/5})}$ . $_ -\lfloor a\rfloor ){\bigr )}}$ jak udowodnili Klaus i Bob co . W szczególności, gdy jest to $,$ liczby całkowitej zmarnowana przestrzeń jest co najmniej proporcjonalna do jej pierwiastka kwadratowego . dokładne asymptotyczne tempo wzrostu zmarnowanej przestrzeni, nawet dla półcałkowitych długości boków, pozostaje problemem otwartym .

Niektóre liczby kwadratów jednostkowych nigdy nie są optymalną liczbą w opakowaniu. W $,$ jeśli kwadrat o rozmiarze $że$ upakowanie tak, ${\ displaystyle a \ geq n}$$kwadratów$ opakowanie jednostkowych .

Kwadratowe opakowanie w kole

Podobnym problemem jest upakowanie n jednostkowych kwadratów w okrąg o jak najmniejszym promieniu. Znane są dobre rozwiązania tego problemu dla n do 35. Oto minimalne rozwiązania dla n do 12:

Liczba kwadratów	Promień okręgu
1	0,707...
2	1.118...
3	1.288...
4	1.414...
5	1.581...
6	1.688...
7	1.802...
8	1.978...
9	2.077...
10	2.121...
11	2.214...
12	2.236...

Zobacz też

• Okrągłe opakowanie w kwadracie
• Kwadratura kwadratu
• Pakowanie prostokątne
• Problem z przesuwaniem sofy

Linki zewnętrzne

• Friedman, Erich , „Kwadraty w kwadratach” , Github , Centrum pakowania Ericha