Kształtowanie impulsu

W elektronice i telekomunikacji kształtowanie impulsów to proces zmiany kształtu fali przesyłanych impulsów w celu optymalizacji sygnału pod kątem zamierzonego celu lub kanału komunikacyjnego . Odbywa się to często poprzez ograniczenie szerokości pasma transmisji i filtrowanie impulsów w celu kontrolowania interferencji międzysymbolowej . Kształtowanie impulsu jest szczególnie ważne w komunikacji RF w celu dopasowania sygnału do określonego pasma częstotliwości i jest zwykle stosowane po kodowaniu linii i modulacji .

Potrzeba kształtowania pulsu

Transmisja sygnału z dużą częstotliwością modulacji przez kanał o ograniczonym paśmie może powodować zakłócenia międzysymbolowe . Powodem tego są korespondencje Fouriera (patrz transformacja Fouriera ). Sygnał o ograniczonym paśmie odpowiada nieskończonemu sygnałowi czasowemu, który powoduje nakładanie się sąsiednich impulsów. Wraz ze wzrostem szybkości modulacji zwiększa się szerokość pasma sygnału. Gdy tylko widmo sygnału jest ostrym prostokątem, prowadzi to do kształtu sinc w dziedzinie czasu. Dzieje się tak, gdy szerokość pasma sygnału jest większa niż szerokość pasma kanału, co prowadzi do zniekształceń. To zniekształcenie zwykle objawia się jako interferencja międzysymbolowa (ISI). Teoretycznie dla impulsów o kształcie sinc nie ma ISI, jeśli sąsiednie impulsy są idealnie wyrównane, tj. w swoich przejściach przez zero. Wymaga to jednak bardzo dobrej synchronizacji i precyzyjnego/stabilnego samplowania bez jittera. Jako praktyczne narzędzie do określania ISI wykorzystuje się tzw Wzór oczu , który wizualizuje typowe efekty kanału i stabilność synchronizacji/częstotliwości.

Widmo sygnału jest określone przez schemat modulacji i szybkość transmisji danych używaną przez nadajnik, ale można je modyfikować za pomocą filtra kształtującego impulsy. To kształtowanie impulsu sprawi, że widmo będzie gładkie, prowadząc ponownie do sygnału ograniczonego w czasie. Zwykle przesyłane symbole są reprezentowane jako sekwencja czasowa diraca delta pomnożona przez symbol. Jest to formalne przejście z domeny cyfrowej do analogowej. W tym momencie przepustowość sygnału jest nieograniczona. Ten teoretyczny sygnał jest następnie filtrowany za pomocą filtra kształtującego impulsy, wytwarzając przesyłany sygnał. Jeśli filtr kształtujący impulsy jest prostokątny w dziedzinie czasu (jak to się zwykle robi podczas rysowania), prowadziłoby to do nieograniczonego widma.

W wielu systemach komunikacyjnych pasma podstawowego filtr kształtujący impulsy jest pośrednio filtrem typu boxcar . Jego transformata Fouriera ma postać sin(x)/x i ma znaczną moc sygnału przy częstotliwościach wyższych niż szybkość symboli. To nie jest duży problem, gdy światłowód lub nawet skrętka jest używana jako kanał komunikacyjny. Jednak w komunikacji RF spowodowałoby to marnowanie przepustowości, a do pojedynczych transmisji wykorzystywane są tylko ściśle określone pasma częstotliwości. Innymi słowy, kanał dla sygnału jest ograniczony pasmem. Dlatego opracowano lepsze filtry, które próbują zminimalizować przepustowość potrzebną dla określonej szybkości symboli.

Przykładem w innych obszarach elektroniki jest generowanie impulsów, w których czas narastania musi być krótki; jednym ze sposobów na to jest rozpoczęcie od wolniej narastającego impulsu i zmniejszenie czasu narastania, na przykład za pomocą diody odzyskiwania stopniowego .

Te opisy tutaj zapewniają praktyczną wiedzę, która obejmuje większość skutków, ale nie obejmuje przyczynowości, która prowadziłaby do funkcji/sygnałów analitycznych. Aby to w pełni zrozumieć, potrzebna jest transformata Hilberta , który indukuje kierunek przez splot z jądrem Cauchy'ego. To łączy rzeczywistą i urojoną część opisu pasma podstawowego, dodając w ten sposób strukturę. To natychmiast implikuje, że albo część rzeczywista, albo część urojona są wystarczające do opisania sygnału analitycznego. Mierząc oba w hałaśliwym otoczeniu, uzyskuje się redundancję, którą można wykorzystać do lepszej rekonstrukcji oryginalnego sygnału. Fizyczna realizacja jest zawsze przyczynowa, ponieważ sygnał analityczny przenosi informację.

Filtry kształtujące impuls

Typowy sygnał zakodowany w NRZ jest niejawnie filtrowany za pomocą filtra sinc.

Nie każdy filtr może być użyty jako filtr kształtujący impuls. Sam filtr nie może wprowadzać interferencji międzysymbolowej — musi spełniać określone kryteria. Kryterium ISI Nyquista jest powszechnie stosowanym kryterium oceny, ponieważ wiąże widmo częstotliwości sygnału nadajnika z interferencją międzysymbolową.

Przykładami filtrów kształtujących impulsy, które są powszechnie spotykane w systemach komunikacyjnych, są:

dopasowanym filtrem po stronie odbiornika, aby osiągnąć optymalną tolerancję na szum w systemie. W tym przypadku kształtowanie impulsu jest równomiernie rozłożone między filtrami nadawczymi i odbiorczymi. Odpowiedzi amplitudowe filtrów są zatem punktowymi pierwiastkami kwadratowymi filtrów systemowych.

Wynaleziono inne podejścia, które eliminują złożone filtry kształtujące impulsy. W OFDM nośne są modulowane tak wolno, że na każdą nośną praktycznie nie ma wpływu ograniczenie szerokości pasma kanału.

Filtr Sinc

Odpowiedź amplitudowa filtra podniesionego cosinusa z różnymi współczynnikami roll-off

Jest również nazywany filtrem Boxcar, ponieważ jego odpowiednikiem w dziedzinie częstotliwości jest prostokątny kształt. Teoretycznie najlepszym filtrem kształtującym impuls byłby filtr sinc, ale nie można go dokładnie zaimplementować. Jest to filtr bezprzyczynowy ze stosunkowo wolno rozkładającymi się ogonami. Jest to również problematyczne z punktu widzenia synchronizacji, ponieważ każdy błąd fazy powoduje gwałtowny wzrost interferencji międzysymbolowej.

Filtr z podniesionym cosinusem

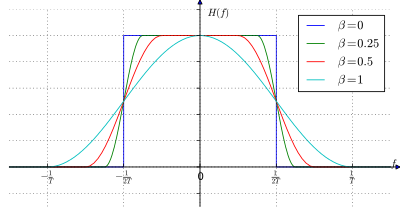
Podniesiony cosinus jest podobny do sinc, z kompromisem mniejszych listków bocznych dla nieco większej szerokości widmowej. Filtry z podniesionym cosinusem są praktyczne w implementacji i są szeroko stosowane. Mają konfigurowalną nadwyżkę pasma, więc systemy komunikacyjne mogą wybrać kompromis między prostszym filtrem a wydajnością widmową.

Filtr Gaussa

Daje to impuls wyjściowy w kształcie funkcji Gaussa .

Zobacz też

John G. Proakis , „ Komunikacja cyfrowa, wydanie 3 ”, rozdział 9, McGraw-Hill Book Co., 1995 . ISBN 0-07-113814-5
Samouczek dotyczący generatora sygnału National Instruments, kształtowanie impulsów w celu poprawy wydajności widmowej
Samouczek dotyczący podstaw pomiarów National Instruments, filtrowanie kształtu impulsu w systemach komunikacyjnych
Root Raised Cosinus Filters & Pulse Shaping in Communication Systems autorstwa Erkina Cubukcu (ntrs.nasa.gov).