Lista drugich momentów powierzchni

Poniżej znajduje się lista drugich momentów powierzchni niektórych kształtów. Drugi moment powierzchni , znany również jako moment bezwładności powierzchni, jest właściwością geometryczną powierzchni, która odzwierciedla rozkład jej punktów względem dowolnej osi. Jednostką wymiaru drugiego momentu powierzchni jest długość do czwartej potęgi, L ⁴ , i nie należy jej mylić z masowym momentem bezwładności . Jeśli jednak kawałek jest cienki, moment bezwładności masy jest równy gęstości powierzchni pomnożonej przez moment bezwładności powierzchni.

Drugie momenty obszaru

Proszę zwrócić uwagę, że dla drugiego momentu równań powierzchni w poniższej tabeli:

\ Displaystyle I_ {x} = \ iint _ {A} y ^ {2} \, dx \, dy}

I

{\ Displaystyle I_ {y} = \ iint _ {A} x ^ {2} \, dx \, dy.}

Opis	Drugi moment obszaru	Komentarz
Wypełniony okrągły obszar o promieniu r	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {\ pi} {4}} r ^ { 4}\\[3pt]I_{y}&={\frac {\pi }{4}}r^{4}\\[3pt]I_{z}&={\frac {\pi }{2} }r^{4}\end{wyrównane}}}$	${\ displaystyle I_ {z}}$ to drugi biegunowy moment obszaru .
Pierścień o promieniu wewnętrznym r 1 _i promieniu zewnętrznym r ₂	${\ Displaystyle {\ rozpocząć {wyrównane }I_{x}&={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)\\[3pt] I_{y}&={\frac {\pi}{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)\\[3pt]I_ {z}&={\frac {\pi}{2}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)\end{wyrównane}}}$	W przypadku cienkich rur ${\ Displaystyle r \ równoważnik r_ {1} \ około r_ {2}}$ i ${\ Displaystyle r_ {2} \ równoważnik r_ {1} + t}$ . Tak więc dla cienkiej rurki ${\ Displaystyle I_ {x} = I_ {y} \ około \ pi r ^ {3} t}$ . ${\ displaystyle I_ {z}}$ jest drugim biegunowym momentem obszaru .
Wypełniony okrągły sektor o kącie θ w radianach i promieniu r względem osi przechodzącej przez środek ciężkości sektora i środek okręgu	${\ Displaystyle I_ {x} = \ lewo (\ teta - \ sin \ teta \ prawo) {\ Frac {r ^ {4}} {8}}}$	Ta formuła jest ważna tylko dla 0 ≤ ${\ textstyle \ theta}$ ≤ ${\ textstyle 2 \ pi}$
Wypełnione półkole o promieniu r względem poziomej linii przechodzącej przez środek ciężkości obszaru	$\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} i = \ lewo ({\ Frac {\ pi}} 8}}-{\frac {8}{9\pi}}\right)r^{4}\około 0,1098r^{4}\\[3pt]I_{y}&={\frac {\pi r ^{4}}{8}}\end{wyrównane}}}$
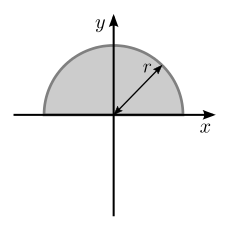
Wypełnione półkole jak wyżej, ale względem osi współliniowej z podstawą	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {\ pi r ^ {4}} {8}} \\ [3pt] I_{y}&={\frac {\pi r^{4}}{8}}\end{wyrównane}}}$	${\ displaystyle I_ {x}}$ : Jest to konsekwencja twierdzenia o osi równoległej i faktu, że odległość między osiami x poprzedniej i tej wynosi ${\ textstyle {\ frac {4r }{3\pi }}}$
Wypełniona ćwiartka koła o promieniu r z osiami przechodzącymi przez podstawy	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {\ pi r ^ {4}} {16}} \\ [3pt] I_{y}&={\frac {\pi r^{4}}{16}}\end{wyrównane}}}$
Wypełniona ćwiartka koła o promieniu r z osiami przechodzącymi przez środek ciężkości	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = \ left({\frac {\pi }{16}}-{\frac {4}{9\pi}}\right)r^{4}\około 0,0549r^{4}\\[3pt]I_{y }&=\left({\frac {\pi }{16}}-{\frac {4}{9\pi }}\right)r^{4}\około 0,0549r^{4}\end{wyrównane }}}$	Jest to konsekwencją twierdzenia o równoległych osiach i faktu, że odległość między tymi dwiema osiami wynosi ${\ textstyle {\ frac {4r} {3 \ pi}}}$
Wypełniona elipsa , której promień wzdłuż osi x wynosi a , a promień wzdłuż osi y wynosi b	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {\ pi} {4}} ab ^ {3} \\[ 3pt]I_{y}&={\frac {\pi }{4}}a^{3}b\end{wyrównane}}}$
Wypełniony prostokątny obszar o szerokości podstawy b i wysokości h	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {bh ^ {3}} {12}} \\ [3pt] I_ { y}&={\frac {b^{3}h}{12}}\end{wyrównane}}}$
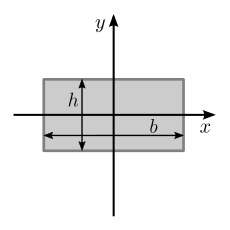
Wypełniony prostokątny obszar jak powyżej, ale względem osi współliniowej z podstawą	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {bh ^ {3}} {3}} \\ [3pt] I_ { y}&={\frac {b^{3}h}{3}}\end{wyrównane}}}$	Wynika to z twierdzenia o osiach równoległych
Wydrążony prostokąt z wewnętrznym prostokątem o szerokości b ₁ i wysokości h ₁	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} i = {\ Frac {bh ^ {3} -b_{1}{h_{1}}^{3}}{12}}\\[3pt]I_{y}&={\frac {b^{3}h-{b_{1}}^{ 3}h_{1}}{12}}\end{wyrównane}}}$
Wypełniony trójkątny obszar o szerokości podstawy b , wysokości h i przemieszczeniu górnego wierzchołka a , względem osi przechodzącej przez środek ciężkości	$\ Displaystyle {\ rozpocząć {wyrównane} I_ { x}&={\frac {bh^{3}}{36}}\\[3pt]I_{y}&={\frac {b^{3}hb^{2}ha+bha^{2} }{36}}\\[3pt]I_{xy}&=-{\frac {bh^{2}}{72}}(b-2a)\end{wyrównane}}}$
Wypełniony trójkątny obszar jak powyżej, ale względem osi współliniowej z podstawą	${\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {bh ^ {3}}} 12}}\\[3pt]I_{y}&={\frac {b^{3}h+b^{2}ha+bha^{2}}{12}}\end{wyrównane}}}$	Jest to konsekwencja twierdzenia o osiach równoległych
Równomierny kąt, powszechnie spotykany w zastosowaniach inżynierskich	${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} = I_ {y} & = {\ Frac {t (5L ^ {2} -5Lt + t ^ {2}) (L^{2}-Lt+t^{2})}{12(2L-t)}}\\[3pt]I_{(xy)}&={\frac {L^{2}t(Lt )^{2}}{4(t-2L)}}\\[3pt]I_{a}&={\frac {t(2L-t)(2L^{2}-2Lt+t^{2} )}{12}}\\[3pt]I_{b}&={\frac {t(2L^{4}-4L^{3}t+8L^{2}t^{2}-6Lt^{ 3}+t^{4})}{12(2L-t)}}\end{wyrównane}}}$	${\ Displaystyle I_ {(xy)}}$ jest często nieużywanym „drugim momentem powierzchni iloczynu”, używanym do definiowania głównych osi

Regularne wielokąty
Opis	Postać	Drugi moment obszaru	Komentarz
Wypełniony regularny (równoliterowy) trójkąt o długości boku a		${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} i = {\ Frac {a ^ {4}} {32 {32 { \sqrt {3}}}}\około 0,01804a^{4}\\[3pt]I_{y}&={\frac {a^{4}}{32{\sqrt {3}}}}\około 0,01804a^{4}\end{wyrównane}}}$	Wynik jest ważny zarówno dla osi poziomej, jak i pionowej przechodzącej przez środek ciężkości, a zatem jest również ważny dla osi o dowolnym kierunku, która przechodzi przez początek układu współrzędnych. Dotyczy to wszystkich regularnych wielokątów .
Wypełniony kwadrat o boku długości a		${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} & = {\ Frac {a ^ {4}} {12}} \\ [3pt] I_ {y} &={\frac {a^{4}}{12}}\end{wyrównane}}}$	Wynik jest ważny zarówno dla osi poziomej, jak i pionowej przechodzącej przez środek ciężkości, a zatem jest również ważny dla osi o dowolnym kierunku, która przechodzi przez początek układu współrzędnych. Dotyczy to wszystkich regularnych wielokątów .
Wypełniony sześciokąt foremny o boku długości a		${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} i = {\ Frac {5 {\ sqrt {3} }}{16}}a^{4}\około 0,54126a^{4}\\[3pt]I_{y}&={\frac {5{\sqrt {3}}}{16}}a^{ 4}\około 0,54126a^{4}\end{wyrównane}}}$	Wynik jest ważny zarówno dla osi poziomej, jak i pionowej przechodzącej przez środek ciężkości, a zatem jest również ważny dla osi o dowolnym kierunku, która przechodzi przez początek układu współrzędnych. Dotyczy to wszystkich regularnych wielokątów .
Wypełniony ośmiokąt foremny o boku długości a		${\ Displaystyle {\ rozpocząć {wyrównane} I_ {x} i = {\ Frac {11 + 8 {\sqrt {2}}}{12}}a^{4}\około 1,85947a^{4}\\[3pt]I_{y}&={\frac {11+8{\sqrt {2}} }{12}}a^{4}\około 1,85947a^{4}\end{wyrównane}}}$	Wynik jest ważny zarówno dla osi poziomej, jak i pionowej przechodzącej przez środek ciężkości, a zatem jest również ważny dla osi o dowolnym kierunku, która przechodzi przez początek układu współrzędnych. Dotyczy to wszystkich regularnych wielokątów .

Twierdzenie o równoległych osiach

Twierdzenie o równoległych osiach można wykorzystać do określenia drugiego momentu pola powierzchni ciała sztywnego wokół dowolnej osi, biorąc pod uwagę drugi moment pola pola ciała wokół osi równoległej przechodzącej przez środek ciężkości ciała, pole przekroju poprzecznego i odległość prostopadłą ( d ) między osiami.

{\ Displaystyle I_ {x '} = I_ {x} + reklama ^ {2}}

Zobacz też