Lista kształtów ze znaną stałą upakowania

Stała upakowania bryły geometrycznej jest największą średnią gęstością osiągniętą przez układy upakowania przystających kopii bryły. Dla większości ciał wartość stałej upakowania jest nieznana. Poniżej znajduje się lista ciał w przestrzeniach euklidesowych, których stała upakowania jest znana. Fejes Tóth udowodnił, że na płaszczyźnie punktowo symetryczne ciało ma stałą upakowania równą jego translacyjnej stałej upakowania i jego kraty stała pakowania. Dlatego każde takie ciało, dla którego wcześniej znana była stała upakowania sieci, na przykład dowolna elipsa , ma w konsekwencji znaną stałą upakowania. Oprócz tych ciał prawie dokładnie znane są stałe upakowania hipersfer w 8 i 24 wymiarach.

Obraz	Opis	Wymiar	Stała pakowania	Uwagi
	Wszystkie kształty, które wypełniają przestrzeń	Wszystko	1	Zgodnie z definicją
	Koło , elipsa	2	π / √ 12 ≈ 0,906900	Dowód przypisywany Thue
	Zwykły pięciokąt	2	${\ Displaystyle {\ Frac {5- {\ sqrt {5}}} {3}} \ około 0,92131}$	Thomasa Halesa i Wödena Kusnera
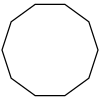
	Wygładzony ośmiokąt	2	${\ Displaystyle \ eta _ {więc} = {\ Frac {8-4 {\ sqrt {2}} - \ ln {2}} 2{\sqrt {2}}-1}}\około 0,902414}$	Reinhardta
	Wszystkie 2-krotnie symetryczne wypukłe wielokąty	2		Algorytm czasu liniowego (w liczbie wierzchołków) podany przez Mounta i Ruth Silvermanów
	Kula	3	π / √ 18 ≈ 0,7404805	Zobacz hipotezę Keplera
	Bi-nieskończony cylinder	3	π / √ 12 ≈ 0,906900	Bezdka i Kuperberga
	Pół-nieskończony cylinder	3	π / √ 12 ≈ 0,906900	Wöden Kusner
	Wszystkie kształty zawarte w rombowym dwunastościanie , którego wpisana kula jest zawarta w kształcie	3	Ułamek objętości dwunastościanu rombowego wypełniony tym kształtem	Następstwo hipotezy Keplera . Przykłady na ilustracji: ośmiościan rombowy i enneakontahedr rombowy .
	hipersfera	8	${\ Displaystyle {\ Frac {({\ Frac {\ pi}} {2}}) ^ {4}} {4!}} \ około 0,2536695}$	Zobacz pakowanie Hypersphere
	hipersfera	24	${\ Displaystyle {\ Frac {({\ Frac {\ pi}} {2}}) ^ {12}} {12!}} \ około 0,000000471087}$	Zobacz pakowanie Hypersphere