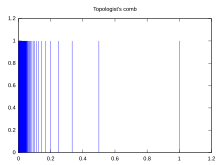
Miejsce na grzebień

W $,$ zwłaszcza w topologii , przestrzeń grzebieniowa szczególna podprzestrzeń przypominająca grzebień . Przestrzeń grzebieniowa ma właściwości, które służą jako szereg kontrprzykładów . Krzywa sinusoidalna topologa ma podobne właściwości do przestrzeni grzebieniowej. Usunięta przestrzeń grzebieniowa jest odmianą przestrzeni grzebieniowej.

Grzebień topologa

Skomplikowany podwójny grzebień dla r=3/4.

Definicja formalna

Rozważmy jego standardową $topologię$ i K będzie zbiorem ${\ Displaystyle \ {1/n ~ | ~ n \ w \ mathbb {N} \}}$ . Zbiór C zdefiniowany przez:

{\ Displaystyle (\ {0 \} \ razy [0,1]) \ kubek (K \ razy [0,1])\szklanka ([0,1]\razy \{0\})}

rozpatrywana jako podprzestrzeń wyposażona w $topologię$ podprzestrzeni jest znana przestrzeń grzebieniowa Usunięta przestrzeń grzebieniowa D jest zdefiniowana przez:

{\ Displaystyle \ {(0,1) \} \ kubek (K \ razy [0,1]) \ kubek ([0,1]\razy \{0\})}

.

usuniętym odcinkiem linii ${\ Displaystyle \ {0 \} \ razy [0,1)} .$

Właściwości topologiczne

Przestrzeń grzebieniowa i usunięta przestrzeń grzebieniowa mają pewne interesujące właściwości topologiczne, głównie związane z pojęciem łączności .

1. Przestrzeń grzebieniowa C jest połączona ścieżkami i kurczliwa , ale nie jest lokalnie kurczliwa, lokalnie połączona ścieżkami ani lokalnie spójna.

2. Usunięta przestrzeń grzebieniowa D jest połączona:

Niech E będzie przestrzenią grzebieniową bez

E

jest również połączoną ścieżką, a

}

przestrzenią

grzebieniową Ponieważ

subset

zamknięcie E, gdzie jest połączone, usunięta przestrzeń grzebieniowa jest również połączona.

3. Usunięta przestrzeń grzebieniowa nie jest połączona ścieżką, ponieważ nie ma ścieżki od (0,1) do (0,0):

Załóżmy, że istnieje ścieżka od p = (0, 1) do punktu (0, 0) w D . Niech ƒ : [0, 1] → D będzie tą ścieżką. Udowodnimy, że ƒ ⁻¹ { p } jest zarówno otwarte , jak i domknięte w [0, 1], zaprzeczając spójności tego zbioru. Oczywiście mamy ƒ ⁻¹ { p } jest domknięte w [0, 1 ] ciągłością ƒ . Aby udowodnić, że ƒ ⁻¹ { p } jest otwarte, postępujemy w następujący sposób: Wybierz otoczenie V (otwarte w R ² ) wokół p , które nie przecina osi x . Załóżmy, że x jest dowolnym punktem w ƒ ⁻¹ { p }. Oczywiście fa ( x ) = p . Wtedy, ponieważ f ⁻¹ ( V ) jest otwarty, istnieje element bazowy U zawierający x taki, że ƒ ( U ) jest podzbiorem V . Zakładamy, że ƒ ( U ) = { p } co będzie oznaczać, że U jest otwartym podzbiorem ƒ ⁻¹ { p } zawierającym x . Ponieważ x było dowolne, ƒ ⁻¹ { p } będzie wtedy otwarte. Wiemy, że U jest spójny, ponieważ jest elementem bazowym topologii porządku na [0, 1]. Dlatego ƒ ( U ) jest spójny. Załóżmy, że ƒ ( U ) zawiera punkt s inny niż p . Wtedy s = (1/ n , z ) musi należeć do D . Wybierz r takie, że 1/( n + 1) < r < 1/ n . Ponieważ ƒ ( U ) nie przecina osi x , zbiory ZA = (−∞, r ) ×

{\ Displaystyle \ mathbb {R}}

i b = ( r , + ∞) ×

{\ displaystyle \ mathbb {R} }

utworzy separację na f ( U ); sprzeczne z powiązaniem f ( U ). Dlatego f ⁻¹ { p } jest zarówno otwarte, jak i domknięte w [0, 1]. To jest sprzeczność.

4. Przestrzeń grzebieniowa jest homotopijna do punktu, ale nie dopuszcza odkształcenia cofania się do punktu dla każdego wybranego punktu bazowego.

Zobacz też

Jamesa Munkresa (1999). Topologia (wyd. 2). Sala Prentice'a . ISBN 0-13-181629-2 .

Kiyosi Itô (red.). „Połączenie”. Encyklopedyczny słownik matematyki . Towarzystwo Matematyczne Japonii. {{ cite journal }} : Cite journal wymaga |journal= ( pomoc )