Nieskończona grupa dwuścienna

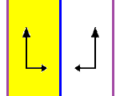
p1m1, ( *∞∞ )	p2, (22∞)	p2mg, (2*∞)
W 2 wymiarach trzy grupy fryzowe p1m1, p2 i p2mg są izomorficzne z grupą Dih ∞ . Wszystkie mają 2 generatory. Pierwsza ma dwie równoległe linie odbicia, druga dwa podwójne zawirowania, a ostatnia ma jedno zwierciadło i jedno podwójne zawirowanie.

W jednym wymiarze nieskończona grupa dwuścienna jest widoczna w symetrii apeirogonu na przemian o dwóch długościach krawędzi, zawierającego punkty odbicia w środku każdej krawędzi.

W matematyce nieskończona grupa dwuścienna Dih _∞ jest grupą nieskończoną o właściwościach analogicznych do właściwości skończonych grup dwuściennych .

W geometrii dwuwymiarowej nieskończona grupa dwuścienna reprezentuje symetrię grupy fryzów , p1m1 , widzianą jako nieskończony zbiór równoległych odbić wzdłuż osi.

Definicja

Każda grupa dwuścienna jest generowana przez obrót r i odbicie; jeśli obrót jest wymierną wielokrotnością pełnego obrotu, to istnieje pewna liczba całkowita n taka, że ​​r ⁿ jest tożsamością, i mamy skończoną grupę dwuścienną rzędu 2 n . Jeśli obrót nie jest wymierną wielokrotnością pełnego obrotu, to nie ma takiego n , a wynikowa grupa ma nieskończenie wiele elementów i nazywa się Dih _∞ . Posiada prezentacje

${\ Displaystyle \ langle r, s \ mid s ^ {2} = 1, srs = r ^ {- 1} \ rangle \, \! }$

${\ Displaystyle \ langle x, y \ mid x ^ {2} = y ^ {2} = 1 \ rangle \, \!}$

i jest izomorficzny z iloczynem półprostym Z i Z /2 oraz z iloczynem swobodnym Z /2 * Z /2. Jest to grupa automorfizmów grafu składającego się ze ścieżki nieskończonej po obu stronach. Odpowiednio, jest to grupa izometrii Z ( patrz także grupy symetrii w jednym wymiarze ), grupa permutacji α: Z → Z spełniająca | ja - j | = |α( ja ) - α( j )|, dla wszystkich ja, j w Z .

Nieskończoną grupę dwuścienną można również zdefiniować jako holomorf nieskończonej grupy cyklicznej .

Aliasowanie

Podczas okresowego próbkowania funkcji sinusoidalnej z szybkością f _s odcięta powyżej reprezentuje jej częstotliwość, a rzędna reprezentuje inną sinusoidę, która może dać ten sam zestaw próbek. Nieskończona liczba odciętych ma tę samą rzędną (klasę równoważności z dziedziną podstawową [0, f _s /2] ) i wykazuje symetrię dwuścienną. Zjawisko „wiele do jednego” jest znane jako aliasing .

Dalsze informacje: Aliasing

Przykładem nieskończonej symetrii dwuściennej jest alias sygnałów o wartościach rzeczywistych.

Podczas próbkowania funkcji z częstotliwością f _s (przedziały 1/ f _s ), następujące funkcje dają identyczne zestawy próbek: {sin(2π( f+Nf _s ) t + φ), N = 0, ±1, ±2, ±3,... }. Zatem wykryta wartość częstotliwości f jest okresowa , r = fs _co daje element translacji . Mówi się, że funkcje i ich częstotliwości są aliasami od siebie. Zauważając tożsamość trygonometryczną:

${\ Displaystyle \ sin (2 \ pi (f + Nf_ {s}) t + \ phi) = \ lewo \ {{\ rozpocząć {tablica} {ll} + \ sin ( 2\pi (f+Nf_{s})t+\phi ),&f+Nf_{s}\geq 0\\-\sin(2\pi |f+Nf_{s}|t-\phi ),&f+ Nf_{s}<0\\\end{tablica}}\right.}$

  możemy zapisać wszystkie częstotliwości aliasów jako wartości dodatnie: | fa + N fa _s | . Daje to element odbicia ( f ), a mianowicie f ↦ − f . Na przykład dla f 0,6 f _s = i N = −1 , f+Nf _s = −0,4 f _s odpowiada 0,4 f _s , w wyniku czego na rysunku znajdują się dwie czarne kropki po lewej stronie. Pozostałe dwie kropki odpowiadają N = −2 i N = 1 . Jak pokazano na rysunku, istnieją symetrie odbicia przy 0,5 f _s , f _s , 1,5 f _s itd. Formalnie iloraz pod aliasingiem to orbifold [0, 0,5 f _s ], z działaniem Z / 2 w punktach końcowych (punkty orbifoldu), odpowiadające odbiciu.

Zobacz też

• Grupa ortogonalna O (2), kolejne nieskończone uogólnienie skończonych grup dwuściennych
• Afiniczna grupa symetryczna , rodzina grup obejmująca nieskończoną grupę dwuścienną