Nomogram

Typowy nomogram w skali równoległej. Ten przykład oblicza wartość T, gdy S = 7,30 i R = 1,17 są podstawiane do równania. Izopleta przecina skalę dla T na poziomie nieco poniżej 4,65.

Nomogram (z greckiego nomos νόμος , „ prawo” i grammē γραμμή , „linia”), zwany także nomografem , wykresem wyrównania lub abac , jest graficznym urządzeniem liczącym , dwuwymiarowym diagramem zaprojektowanym w celu umożliwienia przybliżonego graficznego obliczenia funkcja matematyczna . Dziedzina nomografii została wynaleziona w 1884 roku przez francuskiego inżyniera Philberta Maurice'a d'Ocagne (1862–1938) i był szeroko stosowany przez wiele lat, aby zapewnić inżynierom szybkie obliczenia graficzne skomplikowanych wzorów z praktyczną precyzją. Nomogramy wykorzystują równoległy układ współrzędnych wymyślony przez d'Ocagne zamiast standardowych współrzędnych kartezjańskich .

Nomogram składa się z zestawu n skal, po jednej dla każdej zmiennej w równaniu. Znając wartości n-1 zmiennych można znaleźć wartość nieznanej zmiennej lub ustalając wartości niektórych zmiennych można zbadać związek między nieustalonymi. Wynik uzyskuje się, kładąc linijkę w poprzek znanych wartości na skalach i odczytując nieznaną wartość z miejsca, w którym przecina ona skalę dla tej zmiennej. Wirtualna lub narysowana linia utworzona przez liniał nazywana jest linią indeksu lub izopletą .

Nomogramy kwitły w wielu różnych kontekstach przez około 75 lat, ponieważ umożliwiały szybkie i dokładne obliczenia przed erą kalkulatorów kieszonkowych. Wyniki z nomogramu uzyskuje się bardzo szybko i niezawodnie, po prostu rysując jedną lub więcej linii. Użytkownik nie musi wiedzieć, jak rozwiązywać równania algebraiczne, wyszukiwać dane w tabelach, korzystać z suwaka logarytmicznego lub zastępować liczby w równaniach, aby uzyskać wyniki. Użytkownik nie musi nawet znać podstawowego równania, które reprezentuje nomogram. Ponadto nomogramy w naturalny sposób zawierają ukrytą lub jawną wiedzę dziedzinową w ich projekt. Na przykład, aby utworzyć większe nomogramy w celu uzyskania większej dokładności, nomograf zwykle obejmuje tylko zakresy skali, które są rozsądne i interesujące dla problemu. Wiele nomogramów zawiera inne przydatne oznaczenia, takie jak etykiety referencyjne i kolorowe obszary. Wszystkie one dostarczają użytecznych drogowskazów dla użytkownika.

Wykres Smitha do obliczania impedancji elektrycznej bez wykreślania wartości; chociaż nie jest nomogramem, opiera się na podobnych zasadach

Podobnie jak suwak logarytmiczny, nomogram jest graficznym analogowym urządzeniem obliczeniowym. Podobnie jak suwak logarytmiczny, jego dokładność jest ograniczona precyzją, z jaką można rysować, odtwarzać, przeglądać i wyrównywać fizyczne oznaczenia. skale urządzenia . Nomogramy są zwykle używane w aplikacjach, dla których zapewniany przez nie poziom dokładności jest wystarczający i użyteczny. Alternatywnie można użyć nomogramu do sprawdzenia odpowiedzi uzyskanej za pomocą dokładniejszego, ale podatnego na błędy obliczenia.

Inne typy kalkulatorów graficznych — takie jak wykresy przechwytywane , diagramy trójliniowe i wykresy heksagonalne — są czasami nazywane nomogramami. Urządzenia te nie spełniają definicji nomogramu jako kalkulatora graficznego, którego rozwiązanie znajduje się za pomocą jednej lub więcej izoplet liniowych.

Opis

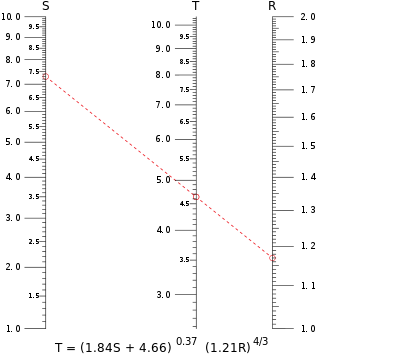
Składniki nomogramu w skali równoległej

Nomogram dla równania z trzema zmiennymi ma zazwyczaj trzy skale, chociaż istnieją nomogramy, w których dwie lub nawet wszystkie trzy skale są wspólne. Tutaj dwie skale reprezentują znane wartości, a trzecia to skala, na której odczytywany jest wynik. Najprostszym takim równaniem jest u ₁ + u ₂ + u ₃ = 0 dla trzech zmiennych u ₁ , u ₂ i u ₃ . Przykład tego typu nomogramu pokazano po prawej stronie, opatrzony terminami używanymi do opisania części nomogramu.

Bardziej skomplikowane równania można czasem wyrazić jako sumę funkcji trzech zmiennych. Na przykład nomogram na górze tego artykułu można skonstruować jako nomogram w skali równoległej, ponieważ można go wyrazić jako taką sumę po zrobieniu logarytmów z obu stron równania.

Skala dla nieznanej zmiennej może leżeć pomiędzy dwoma pozostałymi skalami lub poza nimi. Znane wartości obliczeń zaznacza się na skalach dla tych zmiennych, a pomiędzy tymi znakami rysuje się linię. Wynik jest odczytywany z nieznanej skali w punkcie, w którym linia przecina tę skalę. Skale zawierają „znaczniki”, które wskazują dokładne położenie liczb, a także mogą zawierać oznaczone wartości odniesienia. Skale te mogą być liniowe , logarytmiczne lub mieć bardziej złożone zależności.

Przykładowa izopleta pokazana na czerwono na nomogramie u góry tego artykułu oblicza wartość T , gdy S = 7,30 i R = 1,17. Izopleta przecina skalę dla T na poziomie nieco poniżej 4,65; większa liczba wydrukowana w wysokiej rozdzielczości na papierze dawałaby T = 4,64 z dokładnością do trzech cyfr. Należy zauważyć, że dowolną zmienną można obliczyć na podstawie wartości pozostałych dwóch, co jest cechą nomogramów, która jest szczególnie przydatna w przypadku równań, w których zmienna nie może być algebraicznie odizolowana od innych zmiennych.

Skale proste są przydatne do stosunkowo prostych obliczeń, ale w przypadku bardziej złożonych obliczeń może być wymagane użycie prostych lub skomplikowanych skal zakrzywionych. Nomogramy dla więcej niż trzech zmiennych można konstruować, włączając siatkę skal dla dwóch zmiennych lub łącząc poszczególne nomogramy mniejszej liczby zmiennych w nomogram złożony.

Aplikacje

Nomogramy były używane w szerokiej gamie zastosowań. Próbka zawiera:

Oryginalna aplikacja d'Ocagne, automatyzacja skomplikowanych obliczeń wykopów i nasypów dla usuwania ziemi podczas budowy francuskiego systemu kolei krajowych. Był to ważny dowód słuszności koncepcji, ponieważ obliczenia nie są trywialne, a wyniki przekładają się na znaczne oszczędności czasu, wysiłku i pieniędzy.
Projektowanie kanałów, rur i przewodów do regulacji przepływu wody.
Praca Lawrence'a Hendersona , w której wykorzystano nomogramy do skorelowania wielu różnych aspektów fizjologii krwi. Było to pierwsze poważne zastosowanie nomogramów w Stanach Zjednoczonych, a także pierwsze nomogramy medyczne w dowolnym miejscu. ^{[ potrzebne źródło ]}
Dziedziny medyczne, takie jak farmacja i onkologia.
Obliczenia balistyczne przed systemami kierowania ogniem, gdzie czas obliczeń był krytyczny.
Obliczenia w warsztacie mechanicznym, aby przekonwertować wymiary planu i wykonać obliczenia na podstawie wymiarów i właściwości materiału. Te nomogramy często zawierały oznaczenia standardowych wymiarów i dostępnych produkowanych części.
Statystyki, do skomplikowanych obliczeń właściwości rozkładów oraz do badań operacyjnych, w tym projektowania testów akceptacyjnych do kontroli jakości.
Operations Research, aby uzyskać wyniki w różnych problemach optymalizacyjnych.
Chemia i inżynieria chemiczna, obejmująca zarówno ogólne zależności fizyczne, jak i dane empiryczne dotyczące określonych związków.
Aeronautyka, w której nomogramy były używane przez dziesięciolecia w kokpitach samolotów wszelkiego rodzaju. Jako pomoc w nawigacji i sterowaniu lotem nomogramy były szybkimi, kompaktowymi i łatwymi w użyciu kalkulatorami.
Sputnika 1 po wystrzeleniu przez PE Elyasberga.
Prace inżynierskie wszelkiego rodzaju: projektowanie elektryczne filtrów i linii transmisyjnych, obliczenia mechaniczne naprężeń i obciążeń, obliczenia optyczne i tak dalej.
Wojskowych, gdzie skomplikowane obliczenia muszą być wykonane w terenie szybko iz niezawodnością niezależną od urządzeń elektrycznych.
Sejsmologia , gdzie opracowano nomogramy w celu oszacowania wielkości trzęsienia ziemi i przedstawienia wyników probabilistycznych analiz zagrożenia sejsmicznego

Przykłady

Rezystancja równoległa / cienka soczewka

Równoległy nomogram rezystancji elektrycznej

Poniższy nomogram wykonuje obliczenia:

{\ Displaystyle f (A, B) = {\ Frac {1} {1/A + 1/B}} = {\ ułamek {AB}{A+B}}}

Ten nomogram jest interesujący, ponieważ wykonuje przydatne nieliniowe obliczenia przy użyciu tylko prostych, równomiernie stopniowanych skal. Chociaż linia ukośna ma skalę ${\ displaystyle {\ sqrt {2}}}$ razy większą niż skale osi, liczby na niej dokładnie odpowiadają liczbom bezpośrednio poniżej lub po jej lewej stronie, dzięki czemu można ją łatwo utworzyć, rysując linia prosta po przekątnej na kartce papieru milimetrowego .

A i B , a wynik odczytuje się ze skali diagonalnej. Będąc proporcjonalnym do średniej harmonicznej A i B , ten wzór ma kilka zastosowań. Na przykład jest to wzór na rezystancję równoległą w elektronice i równanie cienkiej soczewki w optyce .

W przykładzie czerwona linia pokazuje, że równoległe rezystory 56 i 42 omów mają łączną rezystancję 24 omów. Pokazuje również, że przedmiot w odległości 56 cm od soczewki o ogniskowej 24 cm tworzy obraz rzeczywisty w odległości 42 cm.

Obliczenia testu chi-kwadrat

Nomogram rozkładu chi-kwadrat

Poniższy nomogram może być użyty do wykonania przybliżonych obliczeń niektórych wartości potrzebnych podczas przeprowadzania znanego testu statystycznego, testu chi-kwadrat Pearsona . Ten nomogram pokazuje użycie zakrzywionych skal z nierównomiernie rozmieszczonymi podziałkami.

Odpowiednie wyrażenie to:

{\ Displaystyle {\ Frac {(OBS-EXP) ^ {2}} {EXP}}}

Skala na górze jest podzielona na pięć różnych zakresów obserwowanych wartości: A, B, C, D i E. Zaobserwowana wartość znajduje się w jednym z tych zakresów, a znacznik użyty na tej skali znajduje się bezpośrednio nad nim. Następnie na podstawie zakresu wybierana jest zakrzywiona skala używana dla wartości oczekiwanej. Na przykład zaobserwowana wartość 9 użyłaby znacznika powyżej 9 w zakresie A, a zakrzywiona skala A byłaby użyta dla wartości oczekiwanej. Zaobserwowana wartość 81 użyłaby znacznika powyżej 81 w zakresie E, a zakrzywiona skala E zostałaby użyta dla wartości oczekiwanej. Pozwala to na włączenie pięciu różnych nomogramów do jednego wykresu.

W ten sposób niebieska linia pokazuje obliczenie:

(9 - 5) ² / 5 = 3,2

a czerwona linia pokazuje obliczenie:

(81 - 70) ² / 70 = 1,7

Podczas przeprowadzania testu często stosuje się poprawkę Yatesa na ciągłość , która polega po prostu na odjęciu 0,5 od obserwowanych wartości. Nomogram do wykonania testu z poprawką Yatesa można skonstruować po prostu przesuwając każdą „obserwowaną” skalę o pół jednostki w lewo, tak aby podziałki 1,0, 2,0, 3,0, ... były umieszczone tam, gdzie wartości 0,5, 1,5, 2,5 , ... pojawiają się na obecnym wykresie.

Ocena ryzyka żywnościowego

Nomogram oceny ryzyka żywności

Chociaż nomogramy reprezentują zależności matematyczne, nie wszystkie są wyprowadzone matematycznie. Poniższy został opracowany graficznie, aby osiągnąć odpowiednie wyniki końcowe, które można łatwo określić na podstawie iloczynu ich relacji w jednostkach subiektywnych, a nie liczbowych. Zastosowanie osi nierównoległych umożliwiło włączenie do modelu zależności nieliniowych.

Liczby w kwadratach oznaczają osie wymagające wprowadzenia po odpowiedniej ocenie.

Para nomogramów na górze obrazu określa prawdopodobieństwo wystąpienia i dostępność, które są następnie włączane do dolnego nomogramu wieloetapowego.

Linie 8 i 10 to „linie wiążące” lub „linie obrotowe” i służą do przejścia między etapami nomogramu złożonego.

Ostatnia para równoległych skal logarytmicznych (12) to nie nomogramy jako takie, ale skale odczytujące, które przekładają wynik ryzyka (11, od odległego do bardzo wysokiego) na częstotliwość próbkowania odpowiednio w celu uwzględnienia aspektów bezpieczeństwa i innych aspektów „ochrony konsumentów” . Ten etap wymaga politycznego „zakupu” w celu zrównoważenia kosztów z ryzykiem. W przykładzie wykorzystano trzyletnią minimalną częstotliwość dla każdego z tych aspektów, przy czym wysokie ryzyko skali jest różne dla obu aspektów, co daje różne częstotliwości dla tych dwóch aspektów, ale oba podlegają ogólnemu minimalnemu pobraniu próbek każdej żywności dla wszystkich aspektów co najmniej raz na trzy lata.

Ten nomogram oceny ryzyka został opracowany przez brytyjską Public Analyst Service przy wsparciu finansowym brytyjskiej Agencji ds. Standardów Żywności do stosowania jako narzędzie do określania odpowiedniej częstotliwości pobierania próbek i analizowania żywności do celów urzędowej kontroli żywności, przeznaczone do oceny wszystkich potencjalnych problemów ze wszystkimi rodzajami żywności, chociaż jeszcze nie przyjęto.

Inne szybkie nomogramy

Za pomocą linijki można łatwo odczytać brakujący wyraz twierdzenia sinusów lub pierwiastki równania kwadratowego i sześciennego .

Nomogram twierdzenia sinusów
Nomogram do rozwiązywania równania kwadratowego x^2+px+q=0
Nomogram do rozwiązywania sześciennego x^3+px+q=0

Zobacz też

Dalsza lektura

DP Adams, Nomografia: teoria i zastosowanie (Archon Books) 1964.
HJ Allcock, J. Reginald Jones i JGL Michel, Nomogram. Teoria i praktyczna konstrukcja wykresów obliczeniowych , wyd. 5, (Londyn: Sir Isaac Pitman & Sons, Ltd.) 1963.
S. Brodestsky, A First Course in Nomography (Londyn, G. Bell and Sons) 1920.
DS Davis, Równania empiryczne i nomografia (Nowy Jork: McGraw-Hill Book Co.) 1943.
M. d'Ocagne: Traité de Nomographie , (Gauthier-Villars, Paryż) 1899.
M. d'Ocagne: (1900) Sur la résolution nomographique de l'équation du septième degré . Comptes rendus (Paryż), 131, 522–524.
RD Douglass i DP Adams, Elementy nomografii (Nowy Jork: McGraw-Hill) 1947.
RP Hoelscher i in., Pomoce graficzne w obliczeniach inżynierskich , (Nowy Jork: McGraw-Hill) 1952.
L. Ivan Epstein, Nomografia , (New York: Interscience Publishers) 1958.
LH Johnson, Nomografia i równania empiryczne , (New York: John Wiley and Sons) 1952.
M. Kattan i J. Marasco. (2010) Co to jest prawdziwy nomogram? , Seminaria z onkologii, 37(1), 23–26.
AS Levens, Nomografia , wyd. 2, (Nowy Jork: John Wiley & Sons, Inc.) 1959.
FT Mavis, The Construction of Nomographic Charts (Scranton, International Textbook) 1939.
E. Otto, Nomografia , (New York: The Macmillan Company) 1963.
HA Evesham Historia i rozwój nomografii (Boston: Docent Press) 2010. ISBN 9781456479626
TH Gronwall, R. Doerfler, A. Gluchoff i S. Guthery, Obliczanie krzywych: matematyka, historia i estetyczny wygląd pracy nomograficznej TH Gronwalla , (Boston: Docent Press) 2012. ISBN 9780983700432

Linki zewnętrzne

Weisstein, Eric W. „Nomogram” . MathWorld .
The Art of Nomography opisuje projektowanie nomogramów przy użyciu geometrii, wyznaczników i przekształceń.
The Lost Art of Nomography to artykuł w czasopiśmie matematycznym poświęcony dziedzinie nomografii.
Nomogramy dla Gier Wojennych , ale także w interesie ogólnym.
PyNomo – oprogramowanie typu open source do konstruowania nomogramów.
Aplet Java do konstruowania prostych nomogramów.
Nomogramy do wizualizacji relacji między trzema zmiennymi - wideo i slajdy z zaproszonej rozmowy Jonathana Rougiera do użytkuR!2011.