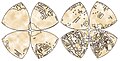
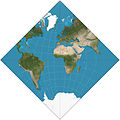
Projekcja mapy wielościennej
Odwzorowanie mapy wielościennej to odwzorowanie mapy oparte na wielościanie kulistym . Zazwyczaj wielościan jest nakładany na kulę ziemską, a każda ściana wielościanu jest przekształcana w wielokąt lub inny kształt na płaszczyźnie. Najbardziej znaną projekcją mapy wielościennej jest mapa Dymaxion Buckminstera Fullera . Kiedy kuliste ściany wielościanu zostaną przekształcone w ściany zwykłego wielościanu, a nie ułożone płasko na płaszczyźnie, efektem będzie wielościenna kula .
Często używanym wielościanem jest bryła platońska lub bryła Archimedesa . Można jednak zastosować inne wielościany: projekcja AuthaGraph wykorzystuje wielościan o 96 ścianach, a projekcja miriaedryczna pozwala na dowolną dużą liczbę ścian. Chociaż przerwy między twarzami są powszechne i coraz częstsze w przypadku rosnącej liczby twarzy, na niektórych mapach ich unika się: projekcja konformalna Lee ma przerwy tylko na granicy, a projekcja AuthaGraph skaluje swoje ściany w taki sposób, że mapa wypełnia prostokąt bez wewnętrznych przerw. Niektóre rzuty można mozaikować w celu wypełnienia płaszczyzny, a wśród nich jest projekcja konforemna Lee.
Do pewnego stopnia wielościan i rzut użyte do przekształcenia każdej ściany wielościanu można rozpatrywać osobno, a niektóre rzuty można zastosować do ścian o różnych kształtach. Rzut gnomoniczny przekształca krawędzie wielościanów sferycznych w linie proste, zachowując wszystkie wielościany zawarte w półkuli, dlatego jest to powszechny wybór. Rzut równopowierzchniowy Snydera można zastosować do dowolnego wielościanu o regularnych ścianach. Rzut zastosowany w późniejszych wersjach mapy Dymaxion można uogólnić na inne ściany trójkąta równobocznego, a nawet na pewne czworoboki.
Projekcje map wielościennych są przydatne do tworzenia dyskretnych globalnych siatek , tak jak w przypadku czworobocznego sześcianu sferycznego i ikozaedrycznej siatki Snydera o równej powierzchni (ISEA).
Historia
Najwcześniejszym znanym rzutem wielościennym jest projekcja oktanowa opracowana przez Leonarda da Vinci lub jego współpracownika około 1514 roku, która przekształca ściany ośmiościanu w trójkąty Reuleaux .
Christian Gottlieb Reichard stworzył wielościenny globus oparty na sześcianie w 1803 r. Dwudziestościenny globus pojawił się w 1851 r. Wielościenne globusy wykonane tanio z tektury były przez pewien czas popularne w Europie.
Projekcje oparte na dwuścianach zaczęły pojawiać się wraz z projekcją pięciokątną Peirce'a w 1879 r., projekcją półkuli w kwadracie Guyou w 1887 r. i projekcją półkuli Adamsa w 1925 r. Chociaż dwuściany nie są tradycyjnymi wielościanami , są to wielościany kuliste , a metody stosowane w tych rzutach są również stosowane w innych rzutach wielościennych. W tej samej pracy, co projekcja półkuli w kwadracie, Adams stworzył mapy przedstawiające cały glob w postaci rombu , sześciokąta i heksagramu .
Bernard JS Cahill wynalazł „mapę motyli” opartą na ośmiościanie w 1909 r. Zostało to uogólnione na projekcję Cahilla – Keyesa w 1975 r. i projekcję motyla Watermana w 1996 r. Praca Cahilla wywarła również wpływ na mapy Dymaxion Fullera: pierwsza wersja Fullera , oparty na sześcianie , został opublikowany w 1943 r., a drugi, oparty na dwudziestościanie, został opublikowany w 1954 r.
W 1965 roku Wellman Chamberlin (znany również ze swojej projekcji trymetrycznej Chamberlina ) i Howard E. Paine z Towarzystwa National Geographic zaprojektowali mapę wielościenną opartą na 12 równych pięciokątnych ścianach dwunastościanu . 20 lat później Chamberlin i Paine wykorzystali tę wielościenną mapę w „Global Pursuit”, grze planszowej przeznaczonej do nauczania dzieci geografii.
Czterostronny sześcian sferyczny został opracowany w 1975 roku na potrzeby projektu Cosmic Tło Explorer .
Galeria
Zobacz też
- HEALPix , który nie jest ściśle odwzorowaniem mapy wielościennej
- Lista odwzorowań map
- ^ a b c d Pędzich, Paweł (2016-12-01). „Obraz świata na mapach wielościennych i globusach” . Polski Przegląd Kartograficzny . 48 (4): 197–210. doi : 10.1515/pcr-2016-0014 . ISSN 2450-6966 . S2CID 133013421 .
- ^ van Wijk, Jarke J. (2008). „Odkrywanie Ziemi: projekcje miriaedryczne” . Dziennik Kartograficzny . 45 (1): 32–42. doi : 10.1179/000870408X276594 . ISSN 0008-7041 . S2CID 218692689 .
- ^ Snyder, John P. (01.03.1992). „Rzutowanie mapy o równym obszarze dla globusów wielościennych” . Cartographica: Międzynarodowe czasopismo informacji geograficznej i geowizualizacji . 29 (1): 10–21. doi : 10.3138/27H7-8K88-4882-1752 . ISSN 0317-7173 .
- ^ Crider, John E. (01.03.2008). „Dokładne równania dla odwzorowania i odwrotności mapy Fullera” . Cartographica: Międzynarodowe czasopismo informacji geograficznej i geowizualizacji . 43 (1): 67–72. doi : 10.3138/carto.43.1.67 . ISSN 0317-7173 .
- ^ Crider, John E. (01.01.2009). „Projekcja mapy geodezyjnej dla czworoboków” . Kartografia i nauka o informacji geograficznej . 36 (2): 131–147. doi : 10.1559/152304009788188781 . ISSN 1523-0406 . S2CID 128390865 .
- ^ Sahr, Kevin; Biały, Denis; Kimerling, AJ (2003). „Geodezyjne dyskretne globalne systemy sieciowe” (PDF) . Kartografia i nauka o informacji geograficznej . 30 (2): 121–134. doi : 10.1559/152304003100011090 . S2CID 16549179 .
- ^ Adams, Oscar S. (1925). Funkcje eliptyczne stosowane na konforemnych mapach świata . Wydanie 297 numeru seryjnego United States Coast and Geodetic Survey. Drukarnia rządu USA.
- ^ LP Lee (1976). „Projekcje konforemne oparte na funkcjach eliptycznych” . Kartografia . 13 (Monografia 16, dodatek nr 1 do kanadyjskiego kartografa).
- ^ Scheel, Eugene (19 maja 2002). „Dzięki intelektowi i artyzmowi Wellman Chamberlin stworzył własny świat” . „Washington Post” .
- ^ „Globalny pościg (1987)” . BoardGameGeek . Źródło 2022-08-30 .
- ^ Chan, FK; O'Neill, EM (1975). Studium wykonalności czterostronnej bazy danych o Ziemi w postaci sferycznej kostki (CSC – Computer Sciences Corporation, raport techniczny EPRF 2-75) (raport techniczny). Monterey, Kalifornia: Ośrodek badawczy zajmujący się prognozami środowiskowymi.
- ^ O'Neill, EM (1976). Rozszerzone badania czterostronnej bazy danych Ziemi w postaci sferycznej kostki (PDF) (raport techniczny). Monterey, Kalifornia: Ośrodek badawczy zajmujący się prognozami środowiskowymi. Zarchiwizowane (PDF) od oryginału w dniu 7 maja 2019 r.