Olog

Aby zapoznać się z tradycyjnymi żeńskimi wspólnymi akademikami ludu Bontoc na Filipinach, zobacz Dap-ay .

Teoria logów jest próbą dostarczenia rygorystycznych ram matematycznych do reprezentacji wiedzy, budowy modeli naukowych i przechowywania danych przy użyciu teorii kategorii , narzędzi lingwistycznych i graficznych. Ologi zostały wprowadzone w 2010 roku przez Davida Spivaka , naukowca z Wydziału Matematyki MIT .

Etymologia

Termin „log” jest skrótem od „ log ontologii ”. „Ontologia” wywodzi się od on- , z greckiego ὤν , ὄντος „byt; to, co jest”, imiesłów teraźniejszy czasownika εἰμί „być” i -λογία , -logia : nauka , badanie , teoria .

Formalizm matematyczny

Log dla danej domeny to $kategoria$ , której obiektami są pola oznaczone frazami dokładniej rzeczownikami nieokreślonymi w liczbie pojedynczej) odpowiednimi dla domeny i których morfizmy są skierowanymi strzałkami między pola, oznaczone frazami czasownikowymi, które również odnoszą się do domeny. Te wyrażenia rzeczownikowe i czasownikowe łączą się, tworząc zdania, które wyrażają relacje między obiektami w domenie.

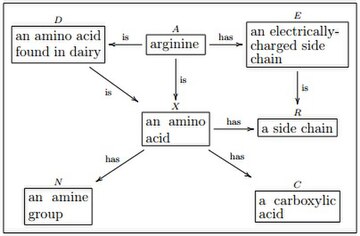
W każdym dzienniku obiekty istnieją w kategorii docelowej . O ile nie określono inaczej, przyjmuje się, że kategorią docelową jest ${\ displaystyle {\ textbf {Zbiór}}}$ , kategoria zestawów i funkcji . Pola na powyższym diagramie reprezentują obiekty ${\ displaystyle {\ textbf {zestaw}}}$ . Na przykład ramka zawierająca frazę „aminokwas” reprezentuje zestaw wszystkich aminokwasów, a ramka zawierająca frazę „łańcuch boczny” reprezentuje zestaw wszystkich łańcuchów bocznych. Strzałka oznaczona „ma”, która wskazuje od „aminokwasu” do „łańcucha bocznego”, przedstawia funkcję, która odwzorowuje każdy aminokwas na jego unikalny łańcuch boczny.

$kategoria$ można użyć, Kleisliego potęgi monady . Za $\ Displaystyle A \ w Ob ({\ textbf {Zestaw}})}$${\ Displaystyle \ mathbb {P} (A)}$ , jest więc zbiorem mocy A Naturalna transformacja odwzorowuje ${\ displaystyle \ eta}$ $\$$Displaystyle$$a \ in A}$ , a naturalna transformacja zbiór zestawów na jego związek Kategoria Kleisli jest kategorią z obiektami pasującymi do tych w , oraz morfizmami, które ustanawiają relacje binarne do ${\ Displaystyle$${\ mathcal {C}} _ ​​{\ mathbb {P}$ . Biorąc pod uwagę morfizm ${\ Displaystyle f: A \ do B}$ i biorąc pod uwagę $\ in B}$${\ Displaystyle b$ , definiujemy morfizm, , że za ∈ ${\ Displaystyle a \ w A$${\ Displaystyle (a, b) \ w R}$ ilekroć ${\ Displaystyle b \ w f (a)}$ . Wyrażenia czasownikowe użyte w tej kategorii docelowej musiałyby mieć sens w przypadku obiektów, które są podzbiorami: na przykład „jest powiązany z” lub „jest większy niż”.

Inną możliwą kategorią docelową jest kategoria rozkładów prawdopodobieństwa Kleisliego, zwana monadą Giry'ego. Zapewnia to uogólnienie procesów decyzyjnych Markowa .

Ologi i bazy danych

Dziennik $danych$ również postrzegać jako schemat bazy . Każde pole (obiekt $)$ w dzienniku jest tabelą, a $strzałki$ (morfizmy) wychodzące z pudełka to kolumny w do ${C}}}$$displaystyle {\ mathcal$ . Przypisanie określonej instancji do obiektu odbywa się $za$ funktora ${\ Displaystyle I: {\ mathcal {C}} \ do {\ textbf {zestaw}}}$ . W powyższym przykładzie ramka „aminokwas” będzie reprezentowana jako tabela, której liczba wierszy jest równa liczbie typów aminokwasów i której liczba kolumn wynosi trzy, po jednej kolumnie dla każdej strzałki wychodzącej z tej ramki.

Relacje między dziennikami

„Komunikacja” między różnymi logami, która w praktyce może być komunikacją między różnymi modelami lub światopoglądami, odbywa się za pomocą funktorów . Spivak tworzy pojęcia „znaczących” i „silnie znaczących” funktorów. Niech $do$ będą dwoma dziennikami, ja $\textbf {Zbiór}}}$${\ displaystyle$$: {\ mathcal {C}} \$ , ${\ Displaystyle J: {\ mathcal {D}} \ do {\ textbf {zestaw}}}$ funktorów (zobacz sekcję dotyczącą dzienników i baz danych) i ${\ displaystyle F: {\ mathcal {C}} \do {\mathcal {D}}}$ funktora. ${\ displaystyle F}$ nazywa się mapowaniem schematu . Mówimy, że ma znaczenie , jeśli istnieje naturalna transformacja $I \ do F ^ {*} J}$$:$ tzw. wycofanie J przez F).

Biorąc za przykład i jako dwa różne modele $displaystyle {$ , funktor ma znaczenie, jeśli „przewidywania”, do ${\$$mathcal {C}}$ które są obiektami w $}$ , wykonanymi przez pierwszy model, można przetłumaczyć na drugi model do ${\ displaystyle {\ mathcal$${$$}}}$ .

Mówimy, że ma duże znaczenie , jeśli dany obiekt ma $X \ w {\ mathcal {C}}}$$displaystyle ja(X)=J(F(X))}$$ja$ X . Ta równość jest równoważna wymaganiu, $.$ był naturalnym izomorfizmem

Czasami trudno będzie znaleźć sensowny funktor od do $C}$$}$$}$ . W takim przypadku możemy ${\ mathcal {B}$ zdefiniować nowy log , który reprezentuje wspólną płaszczyznę i i do ${D}}}$$displaystyle$$}$ i znajdź sensowne funktory $\ mathcal {B}}\do {\mathcal {D}}}$$\ mathcal {B}} \ do {\ mathcal {C}}} i fa re: b → re {\ displaystyle F _ {\ mathcal$ { .

Jeśli komunikacja między logami jest ograniczona do komunikacji dwukierunkowej, jak opisano powyżej, to zbiór logów możemy traktować jako węzły grafu, a krawędzie jako funktory łączące logarytmy. Jeśli dozwolona jest jednoczesna komunikacja między więcej niż dwoma dziennikami, wówczas graf staje się symetrycznym złożonym uproszczeniem .

Zasady dobrych praktyk

Spivak podaje pewne zasady dobrej praktyki pisania dziennika, którego morfizmy mają charakter funkcjonalny (patrz pierwszy przykład w sekcji Formalizm matematyczny). Tekst w ramce powinien być zgodny z następującymi zasadami:

1. zaczynać się od słowa „a” lub „an”. (Przykład: „aminokwas”).
2. odnoszą się do rozróżnienia dokonanego i rozpoznawalnego przez autora logu.
3. odnoszą się do rozróżnienia, dla którego istnieje dobrze zdefiniowany funktor, którego zakres to ${\ displaystyle {\ textbf {Set}}}$ , tj. można udokumentować instancję. (Przykład: istnieje zestaw wszystkich aminokwasów).
4. zadeklarować wszystkie zmienne w strukturze złożonej. $}$ Przykład: zamiast pisać w ramce „mężczyzna i kobieta” napisz „mężczyzna $”$ kobieta $w$ „para ${\ displaystyle (m}$$)$ gdzie $jest$ i jest kobietą").

Pierwsze trzy reguły zapewniają, że obiekty (pola) zdefiniowane przez autora dziennika są dobrze zdefiniowanymi zbiorami. Czwarta zasada poprawia oznakowanie strzałek w dzienniku.

Aplikacje

Koncepcja ta została wykorzystana w artykule opublikowanym w wydaniu BioNanoScience z grudnia 2011 roku przez Davida Spivaka i innych w celu ustalenia naukowej analogii między pajęczym jedwabiem a kompozycją muzyczną.

Zobacz też

• Hipergraf
• Język modelowania
• język ontologii
• Teoria operowa
• Orgologia
• Algebra uniwersalna
• Uniwersalna logika

Linki zewnętrzne

• Spivak, David I. „Informatyka kategoryczna” . math.mit.edu . Źródło 2 maja 2017 r .
•    Spivak, David I. (2014). Teoria kategorii dla nauk . Cambridge, MA: MIT Press . ISBN 9780262028134 . OCLC 876833252 .