Mapa argumentów

Schematyczna mapa argumentów przedstawiająca twierdzenie (lub wniosek), wspierające argumenty i zastrzeżenia oraz zarzut dotyczący wnioskowania
detail of a Tree of Knowledge after Diderot & d'Alembert's Encyclopédie, by Chrétien Frédéric Guillaume Roth
Mapowanie informacji
Tematy i pola
Podejścia łączące węzły
Zobacz też

Mapa argumentów lub diagram argumentów to wizualna reprezentacja struktury argumentu . Mapa argumentów zwykle zawiera kluczowe elementy argumentu, tradycyjnie nazywane wnioskiem i przesłankami , zwanymi także argumentacją i uzasadnieniem . Mapy argumentów mogą również pokazywać współprzesłanki , zarzuty , kontrargumenty , obalenia i lematy . Istnieją różne style mapy argumentów, ale często są one funkcjonalnie równoważne i reprezentują poszczególne twierdzenia argumentu oraz relacje między nimi.

Mapy argumentów są powszechnie używane w kontekście nauczania i stosowania krytycznego myślenia . Celem mapowania jest odkrycie logicznej struktury argumentów, zidentyfikowanie niewypowiedzianych założeń, ocena poparcia, jakie argument oferuje dla konkluzji, oraz pomoc w zrozumieniu debat. Mapy argumentów są często zaprojektowane, aby wspierać rozważania problemów, pomysłów i argumentów w niegodziwych problemach .

Mapy argumentów nie należy mylić z mapą koncepcji lub mapą myśli , dwoma innymi rodzajami diagramów węzeł-połączenie , które mają różne ograniczenia dotyczące węzłów i łączy.

Kluczowe cechy

Zaproponowano wiele różnych rodzajów map argumentów, ale najbardziej powszechny, który Chris Reed i Glenn Rowe nazwali diagramem standardowym , składa się ze struktury drzewiastej z każdym z powodów prowadzących do wniosku. Nie ma zgody co do tego, czy wniosek powinien znajdować się na szczycie drzewa z powodami prowadzącymi do niego, czy też powinien znajdować się na dole z powodami prowadzącymi do niego. Inna odmiana przedstawia argument od lewej do prawej.

Według Douglasa N. Waltona i współpracowników mapa argumentów składa się z dwóch podstawowych elementów: „Jeden element to zestaw liczb w kółku ułożonych w postaci punktów. Każda liczba reprezentuje propozycję (przesłankę lub wniosek) w przedstawianym na diagramie sporze. zestaw linii lub strzałek łączących punkty. Każda linia (strzałka) reprezentuje wnioskowanie. Cała sieć punktów i linii reprezentuje rodzaj przeglądu rozumowania w danym argumencie…” Wraz z wprowadzeniem oprogramowania do tworzenia argumentów map, stało się powszechne, że mapy argumentów składają się z ramek zawierających rzeczywiste twierdzenia, a nie liczb odnoszących się do tych twierdzeń.

Nie ma zgody co do terminologii używanej przy opisywaniu map argumentów, ale standardowy diagram zawiera następujące struktury:

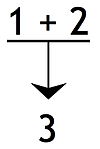
Zależne przesłanki lub współprzesłanki , gdzie co najmniej jedna z połączonych przesłanek wymaga innej przesłanki, zanim będzie mogła uzasadnić wniosek: Argument o tej strukturze został nazwany argumentem połączonym .

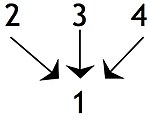
Oświadczenia 1 i 2 to lokale lub współlokale zależne.

Niezależne przesłanki , w przypadku których przesłanka może sama wspierać wniosek: Chociaż niezależne przesłanki łącznie mogą sprawić, że wniosek będzie bardziej przekonujący, należy to odróżnić od sytuacji, w których przesłanka nie daje żadnego poparcia, chyba że jest połączona z inną przesłanką. Tam, gdzie kilka przesłanek lub grup przesłanek prowadzi do ostatecznego wniosku, argument można określić jako zbieżny . Różni się to od rozbieżnego argumentu, w którym pojedyncza przesłanka może być wykorzystana do poparcia dwóch oddzielnych wniosków.

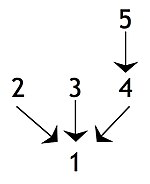
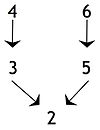
Twierdzenia 2, 3, 4 są niezależnymi przesłankami.

Wnioski pośrednie lub wnioski cząstkowe , gdy twierdzenie jest poparte innym twierdzeniem, które z kolei jest wykorzystywane do poparcia jakiegoś dalszego twierdzenia, tj. wniosku końcowego lub innego wniosku pośredniego: Na poniższym diagramie stwierdzenie 4 jest wnioskiem pośrednim, ponieważ jest konkluzją w stosunku do stwierdzenia 5 , ale jest przesłanką w stosunku do wniosku końcowego, czyli stwierdzenia 1 . Argument o takiej strukturze jest czasem nazywany złożonym . Jeśli istnieje pojedynczy łańcuch twierdzeń zawierający co najmniej jeden wniosek pośredni, argument jest czasami opisywany jako szeregowy lub argument łańcuchowy .

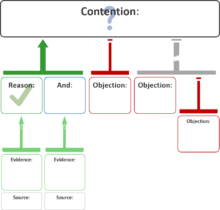
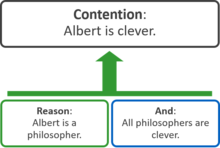
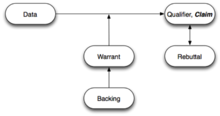
Stwierdzenie 4 jest wnioskiem pośrednim lub wnioskiem cząstkowym.

Każda z tych struktur może być reprezentowana przez równoważne podejście „ramki i linii” do map argumentów. Na poniższym diagramie spór jest pokazany u góry, a połączone z nim ramki przedstawiają powody wspierające , które obejmują jedną lub więcej przesłanek . Zielona strzałka wskazuje, że dwa powody wspierają twierdzenie :

Schemat pudełkowy i liniowy

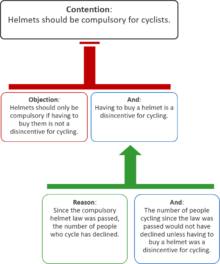
Mapy argumentów mogą również przedstawiać kontrargumenty. Na poniższym diagramie oba zarzuty osłabiają twierdzenie , podczas gdy powody wspierają przesłankę sprzeciwu:

Przykładowy argument wykorzystujący zastrzeżenia

Reprezentowanie argumentu jako mapy argumentów

Diagramowanie tekstu pisanego

Napisany tekst można przekształcić w mapę argumentów, wykonując sekwencję kroków. Książka Monroe Beardsleya z 1950 roku Practical Logic zaleca następującą procedurę:

  1. Oddziel zdania nawiasami i ponumeruj je.
  2. Umieść kółka wokół wskaźników logicznych.
  3. Podaj w nawiasach wszelkie wskaźniki logiczne, które zostały pominięte.
  4. Przedstaw zdania na schemacie, na którym strzałki pokazują zależności między stwierdzeniami.
Schemat przykładu z praktycznej logiki Beardsleya

Beardsley podał pierwszy przykład analizy tekstu w ten sposób:

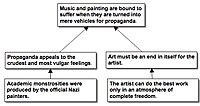
Chociaż ① [ ludzie, którzy mówią o „społecznym znaczeniu” sztuki, nie lubią się do tego przyznawać ] , ② [ muzyka i malarstwo muszą ucierpieć, gdy zamienia się je w zwykłe narzędzia propagandy ] . Za ③ [ propaganda odwołuje się do najbardziej prymitywnych i wulgarnych uczuć ] : (za) ④ [ spójrzcie na akademickie potworności stworzone przez oficjalnych nazistowskich malarzy ] . Co ważniejsze, ⑤ [ sztuka musi być dla artysty celem samym w sobie ] , ponieważ ⑥ [ artysta może wykonywać najlepsze prace tylko w atmosferze pełnej wolności ] .

Beardsley powiedział, że konkluzją w tym przykładzie jest stwierdzenie ②. Oświadczenie ④ należy przepisać jako zdanie oznajmujące, np. „Potworności akademickie [zostały] stworzone przez oficjalnych malarzy nazistowskich”. Stwierdzenie ① wskazuje, że wniosek nie jest akceptowany przez wszystkich, ale stwierdzenie ① zostało pominięte na diagramie, ponieważ nie potwierdza wniosku. Beardsley powiedział, że związek logiczny między stwierdzeniem ③ a stwierdzeniem ④ jest niejasny, ale zaproponował przedstawienie na diagramie stwierdzenia ④ jako stwierdzenia potwierdzającego ③.

Diagram pudełkowy i liniowy przykładu Beardsleya, utworzony przy użyciu procedury Harrella

Niedawno profesor filozofii Maralee Harrell zalecił następującą procedurę:

  1. Zidentyfikuj wszystkie twierdzenia wysuwane przez autora.
  2. Przepisz je jako niezależne stwierdzenia, eliminując nieistotne słowa.
  3. Wskaż, które stwierdzenia są przesłankami, wnioskami cząstkowymi i wnioskiem głównym.
  4. Podaj brakujące, domniemane wnioski i domniemane przesłanki. (Jest to opcjonalne w zależności od celu mapy argumentów).
  5. Umieść stwierdzenia w ramkach i narysuj linię między polami, które są ze sobą połączone.
  6. Wskaż strzałkami wsparcie od przesłanek do (pod)konkluzji.

Diagramowanie jako myślenie

Mapy argumentów są przydatne nie tylko do przedstawiania i analizowania istniejących pism, ale także do przemyślenia problemów w ramach procesu strukturyzowania problemu lub procesu pisania . Wykorzystanie takiej analizy argumentów do przemyślenia problemów nazwano „argumentacją refleksyjną”.

Mapa argumentów, w przeciwieństwie do drzewa decyzyjnego , nie mówi, jak podjąć decyzję, ale proces wyboru spójnej pozycji (lub równowagi refleksyjnej ) w oparciu o strukturę mapy argumentów można przedstawić jako drzewo decyzyjne.

Historia

Filozoficzne korzenie i tradycja mapowania argumentów

Z Whately's Elements of Logic, str. 467, wydanie z 1852 r

W Elements of Logic , opublikowanym w 1826 roku i wydanym w wielu kolejnych wydaniach, arcybiskup Richard Whately podał prawdopodobnie pierwszą formę mapy argumentów, wprowadzając ją z sugestią, że „dla wielu studentów prawdopodobnie uzna to za bardzo jasny i wygodny sposób przedstawiania logiczna analiza toku rozumowania, aby narysować go w postaci drzewa lub podziału logicznego”.

Jednak technika ta nie stała się szeroko stosowana, prawdopodobnie dlatego, że w przypadku złożonych argumentów wymagała dużo pisania i przepisywania przesłanek.

Wykres dowodowy Wigmore'a z 1905 roku

Filozof i teoretyk prawa, John Henry Wigmore, stworzył mapy argumentów prawnych przy użyciu numerowanych przesłanek na początku XX wieku, częściowo opierając się na ideach XIX-wiecznego filozofa Henry'ego Sidgwicka , który użył linii do wskazania relacji między terminami.

Diagramy argumentów anglojęzycznych w XX wieku

Radząc sobie z niepowodzeniem formalnej redukcji nieformalnej argumentacji, anglojęzyczna teoria argumentacji rozwinęła schematyczne podejścia do nieformalnego rozumowania przez okres pięćdziesięciu lat.

Monroe Beardsley zaproponował formę diagramu argumentów w 1950 roku. Jego metoda oznaczania argumentu i przedstawiania jego składowych za pomocą połączonych liczb stała się standardem i jest nadal szeroko stosowana. Wprowadził także wciąż aktualną terminologię opisującą argumenty zbieżne , rozbieżne i szeregowe .

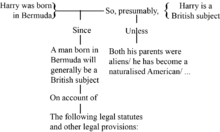
Diagram argumentacji Toulmina , przerysowany na podstawie jego użycia argumentu z 1959 roku
Uogólniony diagram Toulmina

Stephen Toulmin w swojej przełomowej i wpływowej książce The Uses of Argument z 1958 roku zidentyfikował kilka elementów argumentu, które zostały uogólnione. Diagram Toulmina jest szeroko stosowany w krytycznym nauczaniu edukacyjnym. Chociaż Toulmin ostatecznie wywarł znaczący wpływ na rozwój logiki nieformalnej, miał niewielki początkowy wpływ, a podejście Beardsleya do tworzenia diagramów argumentów wraz z jego późniejszym rozwojem stało się standardowym podejściem w tej dziedzinie. Toulmin wprowadził coś, czego brakowało w podejściu Beardsleya. W Beardsley „strzałki łączą powody i wnioski (ale) nie ma żadnego wsparcia dla samej implikacji między nimi. Innymi słowy, nie ma teorii wnioskowania odróżniającej się od logicznej dedukcji, fragment jest zawsze uważany za niekontrowersyjny i nie podlega wsparcie i ocena”. Toulmin wprowadził koncepcję nakazu , który „można uznać za reprezentujący powody wnioskowania, poparcie, które upoważnia do powiązania”.

Podejście Beardsleya zostało udoskonalone przez Stephena N. Thomasa, którego książka z 1973 r. Practical Reasoning In Natural Language wprowadziła termin powiązany z opisem argumentów, w których przesłanki koniecznie współgrały ze sobą, aby poprzeć wniosek. Jednak faktyczne rozróżnienie między zależnymi i niezależnymi przesłankami zostało dokonane wcześniej. Wprowadzenie połączonej struktury umożliwiło mapom argumentów reprezentowanie brakujących lub „ukrytych” przesłanek. Ponadto Thomas zasugerował pokazanie powodów zarówno za , jak i przeciw konkluzji, za pomocą kropkowanych strzałek. Thomas wprowadził termin diagram argumentów i zdefiniował podstawowe racje jako te, które nie zostały poparte przez innych w argumencie, a ostateczny wniosek jako ten, który nie został wykorzystany do poparcia żadnego dalszego wniosku.

Diagram argumentacji Scrivena. Wyraźna przesłanka 1 jest połączona z dodatkowymi nieokreślonymi przesłankami aib, aby implikować 2.

Michael Scriven rozwinął podejście Beardsleya-Thomasa w swojej książce Reasoning z 1976 roku . Podczas gdy Beardsley powiedział: „Najpierw zapisz stwierdzenia… po krótkiej praktyce odnieś się do stwierdzeń tylko według liczb”, Scriven opowiadał się za wyjaśnieniem znaczenia stwierdzeń, wyliczeniem ich, a następnie użyciem diagramu drzewa z liczbami, aby wyświetlić Struktura. Brakujące przesłanki (niesprecyzowane założenia) miały być uwzględnione i oznaczone literą alfabetu zamiast cyfry, aby wyróżnić je ze stwierdzeń jednoznacznych. Scriven przedstawił kontrargumenty w swoich diagramach, które Toulmin zdefiniował jako obalenie. Umożliwiło to również sporządzenie diagramu argumentów dotyczących „równowagi rozważań”.

W 1998 roku seria wielkoskalowych map argumentów wydanych przez Roberta E. Horna wzbudziła powszechne zainteresowanie mapowaniem argumentów.

Opracowanie wspomaganej komputerowo wizualizacji argumentów

Pionier interakcji człowiek-komputer , Douglas Engelbart , w słynnym raporcie technicznym z 1962 r. na temat zwiększania inteligencji szczegółowo przewidywał coś w rodzaju oprogramowania do mapowania argumentów jako integralnej części przyszłych interfejsów komputerowych zwiększających inteligencję:

Zwykle myślisz o sporze jako o sekwencji kolejnych kroków rozumowania, rozpoczynających się od znanych faktów, założeń itp., i zmierzających do konkluzji. Cóż, musimy przemyśleć te kroki w sposób szeregowy i zwykle wymieniamy je w kolejności, kiedy je piszemy, ponieważ tak mniej więcej muszą być przedstawiane w naszych artykułach i książkach — są one dość ograniczające w strukturze symboli, które pozwalają nam korzystać. ... Aby pomóc nam lepiej zrozumieć strukturę argumentu, możemy również wywołać schematyczny lub graficzny wyświetlacz. Po ustaleniu powiązań poprzednik-następnik komputer może automatycznie skonstruować dla nas taki obraz.

- Douglas Engelbart, „Rozwijanie ludzkiego intelektu: ramy koncepcyjne” (1962)

Od połowy do późnych lat 80. opracowano aplikacje oprogramowania hipertekstowego obsługujące wizualizację argumentów, w tym NoteCards i gIBIS ; ten ostatni wygenerował na ekranie graficzną hipertekstową mapę systemu informacyjnego opartego na problemach , model argumentacji opracowany przez Wernera Kunza i Horsta Rittela w latach 70. W latach 90. Tim van Gelder i współpracownicy opracowali szereg aplikacji, które umożliwiały pełne przedstawienie i edycję przesłanek mapy argumentów na diagramie, a nie w legendzie. Pierwszy program Van Geldera, Reason!Able, został zastąpiony dwoma kolejnymi programami, bCisive i Rationale.

W latach 90. i 2000. opracowano wiele innych aplikacji do wizualizacji argumentów. Do 2013 roku istniało ponad 60 takich systemów oprogramowania. W ankiecie przeprowadzonej w 2010 roku na temat argumentacji wspomaganej komputerowo Oliver Scheuer i współpracownicy zauważyli, że jedną z różnic między tymi systemami oprogramowania jest to, czy wspierana jest współpraca. W ich ankiecie systemy argumentacji dla jednego użytkownika obejmowały Convince Me, iLogos, LARGO, Athena, Araucaria i Carneades; systemy argumentacji w małych grupach obejmowały Digalo, QuestMap, Compendium , Belvedere i AcademicTalk; systemy argumentacji społeczności obejmowały Debategraph i Collaboratorium .

Aplikacje

Mapy argumentacyjne zostały zastosowane w wielu obszarach, ale przede wszystkim w środowisku edukacyjnym, akademickim i biznesowym, w tym w uzasadnieniu projektu . Mapy argumentów są również wykorzystywane w kryminalistyce , prawie i sztucznej inteligencji . Zaproponowano również, że mapowanie argumentów ma ogromny potencjał, aby poprawić sposób, w jaki rozumiemy i realizujemy demokrację, w odniesieniu do ciągłej ewolucji e-demokracji .

Trudności z tradycją filozoficzną

Tradycyjnie trudno było oddzielić nauczanie krytycznego myślenia od filozoficznej tradycji nauczania logiki i metody, a większość podręczników krytycznego myślenia została napisana przez filozofów. Nieformalne podręczniki do logiki są pełne przykładów filozoficznych, ale nie jest jasne, czy podejście w takich podręcznikach przenosi się na studentów niefilozoficznych. Wydaje się, że po takich zajęciach efekt statystyczny jest niewielki. Mapowanie argumentów ma jednak wymierny efekt według wielu badań. Na przykład wykazano, że instrukcje dotyczące mapowania argumentów poprawiają umiejętności krytycznego myślenia studentów kierunków biznesowych.

Dowód na to, że mapowanie argumentów poprawia zdolność krytycznego myślenia

Istnieją empiryczne dowody na to, że umiejętności rozwijane na kursach krytycznego myślenia opartych na mapowaniu argumentów w znacznym stopniu przekładają się na krytyczne myślenie bez map argumentów. Metaanaliza Alvareza wykazała, że ​​takie kursy krytycznego myślenia przyniosły korzyści o około 0,70 SD , czyli około dwa razy więcej niż standardowe kursy krytycznego myślenia. Testy użyte w recenzowanych badaniach były standardowymi testami krytycznego myślenia.

Ograniczenia

W przypadku uczniów w szkole mapy argumentów mają ograniczenia. Mogą „wyglądać na zbyt skomplikowanych” i mogą zwiększać obciążenie poznawcze poza to, co jest optymalne do opanowania treści kursu. Tworzenie map wymaga intensywnego coachingu i informacji zwrotnych od doświadczonego twórcy map argumentów. W zależności od celów nauczania, czas poświęcony na szkolenie uczniów w zakresie tworzenia dobrych map może być lepiej wykorzystany na zapoznanie się z treścią kursu zamiast na naukę tworzenia diagramów. Kiedy celem jest zachęcenie uczniów do rozważenia innych perspektyw i kontrargumentów, cel ten można łatwiej osiągnąć za pomocą innych metod, takich jak dyskusja, rubryki i prosta struktura argumentacji lub prosty organizator graficzny , taki jak diagram V. Aby zmaksymalizować mocne strony mapowania argumentów i zminimalizować jego ograniczenia w klasie, należy zastanowić się, na jakim etapie procesu uczenia się potencjalne korzyści z mapowania argumentów przeważą nad jego potencjalnymi wadami.

Normy

Format wymiany argumentów

Główny artykuł: Format wymiany argumentów

Argument Interchange Format, AIF, to międzynarodowy wysiłek mający na celu opracowanie reprezentacyjnego mechanizmu wymiany zasobów argumentacyjnych między grupami badawczymi, narzędziami i domenami przy użyciu bogatego semantycznie języka. AIF-RDF to rozszerzona ontologia reprezentowana w opisu zasobów (RDFS). Chociaż AIF wciąż jest czymś w rodzaju ruchomego celu, to się uspokaja.

Format wymiany wiedzy prawniczej

Główny artykuł: Format wymiany wiedzy prawniczej

Format wymiany wiedzy prawniczej (LKIF) został opracowany w ramach europejskiego projektu ESTRELLA i zaprojektowany w celu stania się standardem przedstawiania i wymiany polityki, prawodawstwa i spraw, w tym ich argumentów uzasadniających, w dziedzinie prawa. LKIF opiera się na języku ontologii sieciowej (OWL) i używa go do reprezentowania pojęć oraz zawiera podstawową ontologię pojęć prawnych wielokrotnego użytku.

Argdown

Argdown to inspirowany Markdownem lekki język znaczników do złożonej argumentacji. Jest przeznaczony do wymiany argumentów i rekonstrukcji argumentów w powszechnie dostępny i czytelny dla człowieka sposób. Składni Argdown towarzyszą narzędzia ułatwiające kodowanie i przekształcanie dokumentów Argdown w mapy argumentów.

Zobacz też

Notatki

Dalsza lektura

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Argument_map&oldid=1134933803 ”