Próbkowanie wielowymiarowe

W cyfrowym przetwarzaniu sygnału próbkowanie wielowymiarowe to proces przekształcania funkcji zmiennej wielowymiarowej w dyskretny zbiór wartości funkcji mierzonych na dyskretnym zbiorze punktów. W artykule przedstawiono podstawowy wynik Petersena i Middletona dotyczący warunków idealnej rekonstrukcji liczbą falową z jej pomiarów na dyskretnej siatce punktów. Wynik ten, znany również jako twierdzenie Petersena – Middletona , jest uogólnieniem twierdzenia o próbkowaniu Nyquista – Shannona do próbkowania jednowymiarowych funkcji o ograniczonym paśmie do wielowymiarowych przestrzeni euklidesowych .

Zasadniczo twierdzenie Petersena-Middletona pokazuje, że funkcję ograniczoną liczbą falową można doskonale zrekonstruować na podstawie jej wartości na nieskończonej siatce punktów, pod warunkiem, że siatka jest wystarczająco drobna. Twierdzenie zapewnia warunki na sieci, w których możliwa jest doskonała rekonstrukcja.

Podobnie jak w przypadku twierdzenia o próbkowaniu Nyquista-Shannona, twierdzenie to zakłada również idealizację dowolnej sytuacji w świecie rzeczywistym, ponieważ ma zastosowanie tylko do funkcji próbkowanych z nieskończonej liczby punktów. Idealna rekonstrukcja jest matematycznie możliwa dla wyidealizowanego modelu, ale jest to tylko przybliżenie dla rzeczywistych funkcji i technik próbkowania, chociaż w praktyce często bardzo dobre.

Czynności wstępne

Ryc. 1: Sześciokątna siatka próbkowania i jej wektory bazowe v ₁ i v ₂ ${\ Displaystyle \ Lambda}$

Ryc. 2: Sieć odwrotna $zachowania$$siatce$ z ryc. 1 i jej wektorom bazowym _{u 1 i u 2} ( _rysunek bez skali )

Pojęcie funkcji o ograniczonym paśmie w jednym wymiarze można uogólnić na pojęcie funkcji o ograniczonej liczbie falowej w wyższych wymiarach. Przypomnijmy, że transformata Fouriera funkcji całkowalnej na n -wymiarowej przestrzeni euklidesowej jest zdefiniowana jako: ${\ Displaystyle f (\ cdot)}$

${\ Displaystyle {\ kapelusz {f}} (\ xi) = {\ mathcal {F}}(f)(\xi )=\int _{\Re ^{n}}f(x)e^{-2\pi i\langle x,\xi \rangle }\,dx}$

gdzie x i ξ to n - $_$ wektory i iloczynem _ _ Mówi się, że funkcja jest ograniczona liczbą falową do zbioru, ${\ Displaystyle f (\$$cdot$ Fouriera spełnia ${\ Displaystyle {\ kapelusz {f}} (\ xi) = 0}$ dla ${\ Displaystyle \ xi \ notin \ Omega}$ .

Podobnie konfigurację równomiernie rozmieszczonych punktów próbkowania w jednym wymiarze można uogólnić na siatkę o wyższych wymiarach. $ja$ zbiorem ${\ Displaystyle \ Lambda = \ lewo \ {\ suma _ {i = 1} ^ {n} a_ {i} v_ {i} \; | \; a_ {i} \ w \ mathbb {Z } \right\}}$ postaci gdzie { v ₁ , ..., v _n } jest podstawą dla ${\ Displaystyle \ Re ^ {n}}$ . Odwrotna krata odpowiadająca jest zdefiniowana przez $displaystyle$$\ Lambda}$

${\ Displaystyle \ Gamma = \ lewo \ {\ suma _ {i = 1} ^ {n} a_ {i} u_ {i} \; | \; a_ {i} \ w \ mathbb {Z } \Prawidłowy\}}$

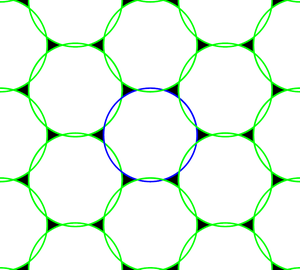
gdzie wektory ${\ Displaystyle \ langle u_ {i}, v_ {j} \ rangle = \ delta _$ wybierane tak, aby spełniały $jot$ . To $jeśli$ wektory tworzą kolumny macierzy i $Displaystyle$ macierzy $są$$}$ następnie ${\ Displaystyle A = B ^ {- T}}$ . Przykładem sieci próbkowania w przestrzeni dwuwymiarowej jest siatka heksagonalna przedstawiona na rysunku 1. Odpowiednia sieć odwrotna jest pokazana na rysunku 2. Odwrotność sieci kwadratowej w dwóch wymiarach jest inną siecią kwadratową. W przestrzeni trójwymiarowej odwrotna siatka sieci sześciennej centrowanej na twarz (FCC) jest siatką sześcienną centrowaną na ciele (BCC).

Twierdzenie

Niech oznacza siatkę w $displaystyle \ Re$$}}$$.$ i odpowiednią siatkę odwrotną Twierdzenie Petersena i Middletona stwierdza, że ​​funkcja $}$ zbioru, może fa $) {\ Displaystyle f (\$ być dokładnie zrekonstruowany na podstawie jego pomiarów na ${\ Displaystyle \ Lambda}$ , że zbiór nie pokrywa się z żadną z jego przesuniętych wersji, $gdzie$ przesunięcie $}$ sieci odwrotności $\ displaystyle \$ . Innymi słowy, $Lambda$ dokładnie zrekonstruować z jego pomiarów na $} pod$ że ${\ Displaystyle \ Omega \ cap \ {x + y: y \ in \ Omega \} = \ pusty zbiór}$ dla wszystkich ${\ Displaystyle x \ in \ Gamma \ setminus \{0\}}$ .

Rekonstrukcja

Ryc. 3: Wsparcie próbkowanego widma $heksagonalne$ funkcji ograniczonej liczbą falową dysk. Niebieskie kółko reprezentuje wsparcie pierwotnego pola ograniczonego liczbą $falową , a zielone kółka reprezentują powtórzenia$ W tym przykładzie powtórzenia widmowe nie nakładają się, a zatem nie występuje aliasing. Oryginalne widmo można dokładnie odzyskać z próbkowanego widma.

Uogólnienie wzoru $z$ Poissona ​​próbki funkcja $Displaystyle f (\ cdot)}$$\$ na siatce wystarczające do stworzenia okresowego sumowania funkcji ${\ Displaystyle {\ kapelusz {f}} (\ cdot)}$ . Wynik to:

${\ Displaystyle {\ kapelusz {f}} _ {s} (\ xi) \ {\ stackrel {\ operatorname {def}}}} \ suma _{y\in \Gamma }{\hat {f}}\left(\xi -y\right)=\sum _{x\in \Lambda }|\Lambda |f(x)\ e^{-i2 \pi \langle x,\xi \rangle },}$

 

 

 

 

()

gdzie ${\ Displaystyle | \ Lambda |}$ reprezentuje objętość równoległościanu utworzonego przez wektory { v ₁ , ..., v _n }. Ta funkcja okresowa jest często określana jako próbkowane widmo i może być interpretowana jako analogia dyskretnej transformaty Fouriera (DTFT) w wyższych wymiarach. Jeśli oryginalne widmo ograniczone liczbą falową jest obsługiwane w zestawie ${\ Displaystyle {\ hat {f}} (\ cdot)}$${\ Displaystyle \ Omega}$ wtedy funkcja jest obsługiwana na okresowych powtórzeniach przesuniętych o punkty ${\ Displaystyle {\ hat {f}} _ {s} (\ cdot$$}$ na odwrotnej siatce ${\ Displaystyle \ Gamma}$ . Jeśli spełnione , to funkcja jest równa ${\ hat {f}} _ {s} (\ xi)}$$)}$$xi$ dla wszystkich dokładnie zrekonstruować z próbek. W tym przypadku zrekonstruowane pole odpowiada pierwotnemu polu i może być wyrażone w kategoriach próbek jako

${\ Displaystyle f (x) = \ suma _ {y \ w \ Lambda} | \ Lambda | f (y) {\ sprawdź {\ chi}} _ {\ Omega }(yx)}$ ,

 

 

 

 

()

gdzie jest $}$ transformatą Fouriera charakterystycznej funkcji zbioru $\ Displaystyle {\ check {\ chi}} _ {\ Omega} (\ cdot)$ { Ten wzór interpolacji jest wielowymiarowym odpowiednikiem wzoru interpolacji Whittakera – Shannona .

Jako przykład załóżmy, że $okrągły$ dysk. $gdy spełnione$ ilustruje wsparcie, warunki twierdzenia Petersena Widzimy, że powtórzenia widmowe nie nakładają się, a zatem oryginalne widmo można dokładnie odzyskać.

Implikacje

Aliasowanie

Główny artykuł: Aliasing

$heksagonalne$ : Wsparcie próbkowanego widma próbkowanie dwuwymiarowej funkcji liczby falowej dysk. W tym przykładzie siatka próbkowania nie jest wystarczająco cienka i dlatego dyski nakładają się na próbkowane widmo. Zatem widma w obrębie $niebieskiego$ nie można dokładnie odzyskać z powodu nakładania się powtórzeń (pokazanych na zielono), co prowadzi do aliasingu.

Ryc. 5: Aliasing przestrzenny w postaci wzoru mory .

Ryc. 6: Prawidłowo pobrany obraz ściany z cegły.

Twierdzenie podaje warunki na siatkach próbkowania dla idealnej rekonstrukcji próbkowanego. Jeśli sieci nie są wystarczająco dokładne, aby spełnić warunek Petersena-Middletona, to ogólnie pola nie można dokładnie zrekonstruować z próbek. W tym przypadku mówimy, że próbki mogą być aliasowane . Ponownie rozważmy przykład, w którym $okrągłym$ dyskiem. Jeśli warunki Petersena-Middletona nie są spełnione, wsparcie próbkowanego widma będzie takie, jak pokazano na rysunku 4. W tym przypadku powtórzenia widma nakładają się, co prowadzi do aliasingu w rekonstrukcji.

Prostą ilustrację aliasingu można uzyskać, badając obrazy o niskiej rozdzielczości. Obraz w skali szarości można interpretować jako funkcję w przestrzeni dwuwymiarowej. Przykład aliasingu pokazano na obrazach wzorów cegieł na rysunku 5. Obraz pokazuje efekty aliasingu, gdy warunek twierdzenia o próbkowaniu nie jest spełniony. Jeśli siatka pikseli nie jest wystarczająco drobna dla danej sceny, pojawia się aliasing, o czym świadczy pojawienie się wzoru mory w otrzymanym obrazie. Obraz na rysunku 6 uzyskuje się, gdy wygładzona wersja sceny jest próbkowana z tą samą siatką. W tym przypadku warunki twierdzenia są spełnione i nie występuje aliasing.

Optymalne sieci próbkowania

Jednym z obiektów zainteresowania przy projektowaniu schematu próbkowania dla pól o ograniczonej liczbie falowej jest identyfikacja konfiguracji punktów, która prowadzi do minimalnej gęstości próbkowania, tj. Gęstości punktów próbkowania na jednostkę objętości przestrzennej w ℜ n {\ $Re ^{n}}$ . Zwykle koszt wykonania i przechowywania pomiarów jest proporcjonalny do zastosowanej gęstości próbkowania. Często w praktyce naturalnym podejściem do próbkowania dwuwymiarowych pól jest próbkowanie ich w punktach na prostokątnej siatce . Jednak nie zawsze jest to idealny wybór pod względem gęstości próbkowania. Twierdzenie Petersena i Middletona można wykorzystać do zidentyfikowania optymalnej sieci dla pól próbkowania, które są ograniczone $zbioru$ . Na przykład można wykazać, że krata $^{2}}$ minimalną gęstością przestrzenną punktów, która pozwala na doskonałe rekonstrukcje pól ograniczonych liczbą falową do okrągłego dysku w $^ {2}}$$displaystyle \ Re$ jest siatką sześciokątną. W konsekwencji sieci sześciokątne są preferowane do próbkowania pól izotropowych w ${\ displaystyle \ Re ^ {2}}$ .

Optymalne sieci próbkowania badano w wyższych wymiarach. Ogólnie rzecz biorąc, optymalne z upakowaniem sfer są idealne do próbkowania gładkich procesów stochastycznych, podczas gdy optymalne sieci pokrywające sfery są idealne do próbkowania zgrubnych procesów stochastycznych.

Ponieważ sieci optymalne są na ogół nierozdzielne, projektowanie filtrów interpolacyjnych i rekonstrukcyjnych wymaga mechanizmów projektowania filtrów niebędących iloczynem tensorowym (tj. nierozdzielnych). Splajny skrzynkowe zapewniają elastyczne ramy do projektowania takich nierozłącznych filtrów FIR do rekonstrukcji , które można geometrycznie dopasować do każdej sieci. Hex-splajny to uogólnienie B-splajnów dla dwuwymiarowych sieci heksagonalnych. Podobnie, w wymiarach 3-D i wyższych, splajny Woronoja zapewniają uogólnienie B-splajnów które można wykorzystać do zaprojektowania nierozdzielnych filtrów FIR, które są geometrycznie dopasowane do dowolnej sieci, w tym sieci optymalnych.

Jawna konstrukcja idealnych filtrów dolnoprzepustowych (tj. funkcji sinc ) uogólnionych na optymalne sieci jest możliwa dzięki zbadaniu właściwości geometrycznych stref Brillouina (tj $powyżej$ ) tych sieci (które są zonotopami ). To podejście zapewnia jawną reprezentację w formie zamkniętej ${\ Displaystyle {\ check {\ chi}} _ {\ Omega} (\ cdot)}$ dla siatek ogólnych, w tym siatek optymalnych do próbkowania. Ta konstrukcja zapewnia uogólnienie filtra Lanczosa w 1-D do ustawienia wielowymiarowego dla optymalnych sieci.

Aplikacje

Twierdzenie Petersena-Middletona jest przydatne w projektowaniu skutecznych strategii rozmieszczania czujników w zastosowaniach obejmujących pomiary zjawisk przestrzennych, takich jak badania sejsmiczne, monitorowanie środowiska i przestrzenne pomiary pola audio.