Próg błędu (ewolucja)

W biologii ewolucyjnej i genetyce populacji próg błędu (lub krytyczny współczynnik mutacji ) jest ograniczeniem liczby par zasad , jakie może mieć samoreplikująca się cząsteczka, zanim mutacja zniszczy informacje w kolejnych generacjach cząsteczki. Próg błędu ma kluczowe znaczenie dla zrozumienia „paradoksu Eigena”.

Próg błędu jest pojęciem dotyczącym początków życia ( abiogenezy ), w szczególności bardzo wczesnego życia, przed pojawieniem się DNA . Postuluje się, że pierwszymi samoreplikującymi się cząsteczkami mogły być małe cząsteczki RNA podobne do rybozymu . Cząsteczki te składają się z ciągów par zasad lub „cyfr”, a ich kolejność jest kodem, który kieruje tym, jak cząsteczka oddziałuje z otoczeniem. Każda replikacja jest obarczona błędem mutacji. Podczas procesu replikacji każda cyfra ma pewne prawdopodobieństwo, że zostanie zastąpiona inną cyfrą, co zmienia sposób, w jaki cząsteczka oddziałuje z otoczeniem i może zwiększać lub zmniejszać jej przydatność lub zdolność do reprodukcji w tym środowisku.

Krajobraz fitness

Główny artykuł: Krajobraz fitness

Manfred Eigen zauważył w swoim artykule z 1971 r. (Eigen 1971), że ten proces mutacji ogranicza liczbę cyfr, jakie może mieć cząsteczka. Jeśli cząsteczka przekroczy ten krytyczny rozmiar, efekt mutacji staje się przytłaczający, a niekontrolowany proces mutacji zniszczy informację w kolejnych generacjach cząsteczki. Próg błędu jest również kontrolowany przez „krajobraz sprawności” cząsteczek. Krajobraz fitness charakteryzuje się dwiema koncepcjami wzrostu (=sprawność) i odległości (=liczba mutacji). Podobne cząsteczki są „blisko” siebie, a cząsteczki, które są lepiej przystosowane niż inne i mają większe szanse na reprodukcję, znajdują się „wyżej” w krajobrazie.

Jeśli określona sekwencja i jej sąsiedzi mają wysokie dopasowanie, utworzą quasigatunek i będą w stanie obsłużyć dłuższe sekwencje niż pasująca sekwencja z kilkoma pasującymi sąsiadami lub mniej dopasowanym sąsiedztwem sekwencji. Ponadto Wilke (Wilke 2005) zauważył, że koncepcja progu błędu nie ma zastosowania w częściach krajobrazu, w których występują śmiertelne mutacje, w których indukowana mutacja daje zerową sprawność i uniemożliwia reprodukcję cząsteczki.

paradoks Eigena

Paradoks Eigena jest jedną z najtrudniejszych zagadek w badaniu pochodzenia życia. Uważa się, że opisana powyżej koncepcja progu błędu ogranicza rozmiar samoreplikujących się cząsteczek do być może kilkuset cyfr, jednak prawie całe życie na Ziemi wymaga znacznie dłuższych cząsteczek do zakodowania informacji genetycznej. Ten problem jest rozwiązywany w żywych komórkach przez enzymy, które naprawiają mutacje, umożliwiając cząsteczkom kodującym osiągnięcie rozmiarów rzędu milionów par zasad. Te duże cząsteczki muszą oczywiście kodować enzymy, które je naprawiają, i na tym polega paradoks Eigena, po raz pierwszy przedstawiony przez Manfreda Eigena w jego artykule z 1971 r. (Eigen 1971). Mówiąc najprościej, paradoks Eigena sprowadza się do:

• Bez enzymów korekcji błędów maksymalny rozmiar replikującej się cząsteczki wynosi około 100 par zasad.
• Aby replikująca się cząsteczka mogła kodować enzymy korygujące błędy, musi być znacznie większa niż 100 zasad.

To paradoks typu kura lub jajko , z jeszcze trudniejszym rozwiązaniem. Co było pierwsze, duży genom czy enzymy korekcji błędów? Zaproponowano szereg rozwiązań tego paradoksu:

• Model korektora stochastycznego (Szathmáry i Maynard Smith, 1995). W tym proponowanym rozwiązaniu pewna liczba prymitywnych cząsteczek, powiedzmy dwóch różnych typów, jest w jakiś sposób związana ze sobą, na przykład przez kapsułkę lub „ścianę komórkową”. Jeśli ich sukces reprodukcyjny zostanie wzmocniony przez, powiedzmy, równą liczbę komórek w każdej komórce, a rozmnażanie zachodzi przez podział, w którym każdy z różnych typów cząsteczek jest losowo rozdzielony między „dzieci”, proces selekcji będzie promował taką równą reprezentację w komórek, nawet jeśli jedna z cząsteczek może mieć selektywną przewagę nad drugą.
• Zrelaksowany próg błędu (Kun i in., 2005) — Badania rzeczywistych rybozymów wskazują, że tempo mutacji może być znacznie mniejsze niż początkowo oczekiwano — rzędu 0,001 na parę zasad na replikację. Może to pozwolić na długość sekwencji rzędu 7-8 tysięcy par zasad, wystarczającą do włączenia podstawowych enzymów korekcji błędów.

Prosty model matematyczny

Rozważmy 3-cyfrową cząsteczkę [A,B,C], gdzie A, B i C mogą przyjmować wartości 0 i 1. Istnieje osiem takich sekwencji ([000], [001], [010], [011] , [100], [101], [110] i [111]). Powiedzmy, że cząsteczka [000] jest najbardziej dopasowana; przy każdej replikacji tworzy średnio $.$ , gdzie $displaystyle a> 1}$ \ Cząsteczka ta nazywana jest „sekwencją główną”. Pozostałe siedem sekwencji jest mniej dopasowanych; każdy z nich wytwarza tylko 1 kopię na replikację. Replikacja każdej z trzech cyfr odbywa się z szybkością mutacji μ. Innymi słowy, przy każdej replikacji cyfry sekwencji istnieje prawdopodobieństwo, $;$ będzie błędna 0 zostanie zastąpione przez 1 lub odwrotnie. Pomińmy podwójne mutacje i śmierć cząsteczek (populacja będzie rosła w nieskończoność) i podzielmy osiem cząsteczek na trzy klasy w zależności od ich odległości Hamminga od sekwencji głównej:

Odległość Hamminga	Sekwencje
0	[000]
1	[001] [010] [100]
2	[110] [101] [011]
3	[111]

$,$ że liczba sekwencji dla odległości d jest po prostu dwumianowym dla wierzchołek L =3 wymiarowy sześcian, gdzie każda krawędź sześcianu określa ścieżkę mutacji, w której zmiana odległości Hamminga wynosi zero lub ±1. Można zauważyć, że na przykład jedna trzecia mutacji cząsteczek [001] wytworzy cząsteczki [000], podczas gdy pozostałe dwie trzecie wytworzą cząsteczki klasy 2 [011] i [101]. Możemy teraz napisać wyrażenie dla populacji potomnych ${$ w kategoriach populacji nadrzędnych $n'_ {i}}$ displaystyle .

${\ Displaystyle n'_ {i} = \ suma _ {j = 0} ^ {3} w_ {ij} n_ {j}}$

gdzie macierz „ w ”, obejmująca dobór naturalny i mutacje, zgodnie z modelem quasi-gatunkowym , jest dana wzorem:

${\ Displaystyle \ mathbf {w} = {\ rozpocząć {bmatrix} a \ cdot Q & 3a \ cdot \ mu & 0 i 0 \\\ mu &Q&2\mu &0\\0&2\mu &Q&\mu \\0&0&3\mu &Q\end{bmacierz}}}$

gdzie $.$ cała Wektory własne macierzy w dadzą liczby populacji równowagi dla każdej klasy. Na przykład, jeśli tempo mutacji μ wynosi zero, będziemy mieli Q=1, a stężenia równowagi będą wynosić ${\ Displaystyle [n_ {0 },n_{1},n_{2},n_{3}]=[1,0,0,0]}$ . Sekwencja główna, która jest najlepiej przystosowana, jako jedyna przetrwa. Jeśli mamy wierność replikacji Q = 0,95 i przewagę genetyczną a = 1,05, to stężenia równowagi będą w przybliżeniu wynosić ${\ Displaystyle [0,33,0,38,0,24,0,06]}$ . Można zauważyć, że sekwencja główna nie jest tak dominująca; niemniej jednak sekwencje o małej odległości Hamminga stanowią większość. Jeśli mamy wierność replikacji Q zbliżającą się do 0, to stężenia równowagi będą w przybliżeniu wynosić ${\ Displaystyle [0,125,0,375,0,375,0,125]}$ . Jest to populacja z równą liczbą każdej z 8 sekwencji. (Gdybyśmy mieli idealnie równe populacje wszystkich sekwencji, mielibyśmy populacje [1,3,3,1]/8.)

Jeśli przejdziemy teraz do przypadku, w którym liczba par zasad jest duża, powiedzmy L=100, otrzymamy zachowanie przypominające przejście fazowe . Poniższy wykres po lewej stronie przedstawia serię stężeń równowagowych podzielonych przez współczynnik dwumianowy ${\ Displaystyle {\ tbinom {100} {k}}}$ . (To mnożenie pokaże populację dla pojedynczej sekwencji w tej odległości i da płaską linię dla równego rozkładu.) Selektywna przewaga sekwencji głównej jest ustawiona na a=1,05. Oś pozioma to odległość Hamminga d . Różne krzywe dotyczą różnych całkowitych wskaźników mutacji ${\ Displaystyle (1-Q)}$ . Widać, że dla niskich wartości całkowitego tempa mutacji populacja składa się z quasi-gatunków skupionych w sąsiedztwie sekwencji wzorcowej. Powyżej całkowitego wskaźnika mutacji około 1-Q=0,05 rozkład szybko się rozprzestrzenia, aby równomiernie zaludnić wszystkie sekwencje. Poniższy wykres po prawej stronie pokazuje ułamkową populację sekwencji głównej jako funkcję całkowitej szybkości mutacji. Ponownie widać, że poniżej krytycznego tempa mutacji około 1-Q = 0,05, sekwencja główna zawiera większość populacji, podczas gdy powyżej tego tempa zawiera tylko około 2 - L ≈ 10 - $- L}\około 10^{-30}}$ całej populacji.

Liczebność populacji jako funkcja odległości Hamminga d i tempa mutacji (1-Q). Oś pozioma d to odległość Hamminga sekwencji molekularnych od sekwencji głównej. Oś pionowa to logarytm populacji dla dowolnej przez _sekwencji w tej odległości podzielony przez całkowitą liczbę ludności (a więc podział nd współczynnik dwumianu). Całkowita liczba cyfr na sekwencję wynosi L=100, a sekwencja główna ma selektywną przewagę a=1,05.

Populacja sekwencji głównej jako ułamek całej populacji ( n ) jako funkcja ogólnego tempa mutacji (1-Q). Całkowita liczba cyfr na sekwencję wynosi L=100, a sekwencja główna ma selektywną przewagę a=1,05. Widzi się, że „przemiana fazowa” zachodzi przy około 1-Q = 0,05.

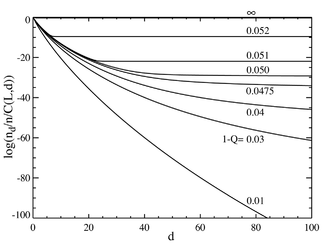
Można zauważyć, że występuje ostre przejście przy wartości 1-Q nieco większej niż 0,05. Dla częstości mutacji powyżej tej wartości populacja sekwencji głównej spada praktycznie do zera. Powyżej tej wartości dominuje.

W granicy, gdy L zbliża się do nieskończoności, system faktycznie ma przejście fazowe przy krytycznej wartości Q: ${\ displaystyle Q_ {c} = 1/a.$ } Można by pomyśleć o ogólnym tempie mutacji (1-Q) jako o rodzaju „temperatury”, która „topi” wierność sekwencji molekularnych powyżej krytycznej „temperatury” 1 - Q do {\ displaystyle $c }}$ . Aby nastąpiła wierna replikacja, informacja musi zostać „zamrożona” w genomie.

Zobacz też

• Katastrofa błędu
• Wir zagłady
• Entropia genetyczna
• Erozja genetyczna
• Zapadka Mullera

•    Eigen, M. (1971). „Samoorganizacja materii i ewolucja makrocząsteczek biologicznych”. Naturwissenschaften . 58 (10): 465–523. Bibcode : 1971NW.....58..465E . doi : 10.1007/BF00623322 . PMID 4942363 . S2CID 38296619 .
• „Teoria quasispecies w kontekście genetyki populacji - Claus O. Wilke” (PDF) . Źródło 12 października 2005 .
•   Campos, PR; Fontanari, JF (1999). „Skalowanie przejścia progu błędu w skończonych rozmiarach w populacjach skończonych” (PDF) . J. Fiz. O: Matematyka. gen . 32 (1): L1–L7. arXiv : cond-mat/9809209 . Bibcode : 1999JPhA...32L...1C . doi : 10.1088/0305-4470/32/1/001 . S2CID 16500591 .
•    Holmes, Edward C. (2005). „O właściwym rozmiarze” . Genetyka przyrody . 37 (9): 923–924. doi : 10.1038/ng0905-923 . PMC 7097767 . PMID 16132047 .
•    Eörs Szathmáry; Johna Maynarda Smitha (1995). „Główne przemiany ewolucyjne”. Natura . 374 (6519): 227–232. Bibcode : 1995Natur.374..227S . doi : 10.1038/374227a0 . PMID 7885442 . S2CID 4315120 .
•    Luisa Villarreala; Guenther Witzany (2013). „Ponowne przemyślenie teorii quasigatunków: od najlepiej przystosowanego typu do współpracujących konsorcjów” . Światowy Dziennik Chemii Biologicznej . 4 (4): 79–90. doi : 10.4331/wjbc.v4.i4.79 . PMC 3856310 . PMID 24340131 .
•    Adam Kun; Mauro Santosa; Eörs Szathmáry (2005). „Prawdziwe rybozymy sugerują złagodzony próg błędu”. Genetyka przyrody . 37 (9): 1008–1011. doi : 10.1038/ng1621 . PMID 16127452 . S2CID 30582475 .