Przesyłki Oceaniczne

OceanParcels , „Prawdopodobnie naprawdę wydajny obliczeniowo symulator Lagrange'a”, to zestaw klas i metod Pythona , który jest używany do śledzenia cząstek takich jak woda, plankton i tworzywa sztuczne. Wykorzystuje dane wyjściowe Ocean General Circulation Models (OGCM) . Głównym celem OceanParcels jest przetwarzanie coraz większych ilości danych zarządzanych przez OGCM. Dynamika przepływu jest symulowana za pomocą modelowania Lagrange'a (obserwator porusza się wraz z cząstką), a geofizyczna dynamika płynów jest symulowana za pomocą modelowania Eulera (obserwator pozostaje nieruchomy) lub dostarczane przez dane eksperymentalne. OceanParcels opiera się na dwóch zasadach, a mianowicie na możliwości odczytu zewnętrznych zestawów danych z różnych formatów oraz konfigurowalnych jądrach w celu zdefiniowania dynamiki cząstek.

Pojęcie

OceanParcels przyjmuje jako dane wejściowe pole przepływu określone metodami Eulera lub dane eksperymentalne (np. uzyskane za pomocą pomiarów naziemnych, zdjęć satelitarnych lub prądów Dopplera). Dane te można podawać na różnych strukturach siatki. Aby uzyskać dane w dowolnym punkcie, stosuje się interpolację . Modelowanie Lagrange'a wykorzystuje dane podane przez pole przepływu i interpolację do symulacji dynamiki obiektu.

Struktura siatki

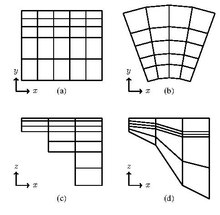
Rysunek 1: Struktury siatki w kierunku poziomym i pionowym.

Rysunek 2: Siatka A (po lewej), siatka B (w środku), siatka C (po prawej)

W płaszczyźnie poziomej, tj. w płaszczyźnie xy, OceanParcels pozwala na prostoliniowe i krzywoliniowe siatki danych (patrz odpowiednio rys. 1 a i b). W płaszczyźnie pionowej, tj. w płaszczyźnie xz, obsługiwane są poziomy z i poziomy s (patrz odpowiednio rys. 1 c i d). Wszystkie cztery kombinacje tych siatek są obsługiwane w przestrzeni trójwymiarowej.

OceanParcels obsługuje również tak zwane schodkowe siatki A, B i C , które są powszechne w modelowaniu oceanów. Uwzględniają one fakt, że różne zmienne mogą być mierzone w różnych punktach siatki. Odpowiednimi zmiennymi w analizie oceanu są prędkość południkowa (v), prędkość strefowa (u) i znaczniki (q). W siatce A wszystkie z nich są oceniane w tych samych punktach siatki. W siatce B u i v są oceniane w punkcie siatki w środku między punktem siatki, w którym oceniana jest T, to znaczy, że istnieją dwie nakładające się siatki. W siatce C wszystkie zmienne są oceniane na własnej siatce, to znaczy, że istnieją trzy nakładające się siatki. Zobacz rysunek 2 dla wizualizacji.

Metody interpolacji

Aby uzyskać dane terenowe w punkcie, który nie znajduje się w węźle siatki, stosuje się metody interpolacji. OceanParcels obsługuje kilka różnych takich metod:

interpolacja liniowa
interpolacja najbliższego sąsiada
interpolacja na siatkach A, B, C.

Modelowanie Lagrange'a

Trajektorię Lagrange'a cząstki można obliczyć, całkując numerycznie po jej położeniu $funkcji$ czasu, określonej przez ${\ Displaystyle X (t_ {2}) = X (t_ {1}) + \ int _ {t_ {1}} ^ {t_ {2}} v (x, \ tau) d \ tau + \ Delta X_ { b}(t_{1})}$ . Tutaj $displaystyle t_ {1}}$ $\$ to czas rozpoczęcia, a czas, w którym oceniana jest pozycja cząstki ${\ Displaystyle v (x, \ tau)}$ jest prędkością cząstki w czasie ${\ Displaystyle \ tau}$ . ${\ Displaystyle \ Delta X_ {b} (t)}$ oddaje ruch cząstki spowodowany jej specyficznymi cechami (np. góra lodowa porusza się inaczej w oceanie niż niezamarznięta masa wody). O ile nie określono inaczej, OceanParcels używa schematu Runge-Kutty czwartego rzędu do integracji tej funkcji. Jako alternatywę, OceanParcels obsługuje integrację Euler-forward lub adaptacyjną integrację Runge-Kutta-Fehlberg .

OceanParcels zapewnia możliwość modelowania indywidualnego zachowania cząstki. Indywidualne zachowanie to zachowanie określone przez cechy cząsteczki, na przykład topnienie gór lodowych i pływanie ryb, co prowadzi do różnej dynamiki. OceanParcels implementuje to za pomocą krótkich fragmentów kodu, które są wykonywane za każdym razem, gdy wykonywany jest ParticleSet (klasa definiująca używane cząstki). Te fragmenty kodu nazywane są jądrami. Niektóre powszechnie używane jądra są predefiniowane w OceanParcels, na przykład jądra modelujące ruchy Browna . Jednak użytkownik może również zdefiniować jądra specyficzne dla problemu. Pozwala to na modelowanie różnych obiektów, których przykłady podano w rozdziale „Aplikacje”. Aby zaimplementować te dostosowane jądra, użytkownik może wybrać między użyciem Pythona z możliwością automatycznego tłumaczenia na C lub użyciem biblioteki C.

Aplikacje

Analiza Lagrange'a może być wykorzystana do symulacji ścieżek wirtualnych cząstek, które mogą reprezentować masy wody, wskaźniki temperatury , wskaźniki zasolenia , wskaźniki składników odżywczych , wodorosty , larwy koralowców, tworzywa sztuczne, ryby , góry lodowe , plankton itp. Ścieżki różnych cząstek mogą być modelowane przy użyciu określonych jąder, na przykład, że ryby mogą pływać i że góry lodowe mogą się topić.

Masy wodne

Ruch mas wody można obliczyć numerycznie za pomocą pól prędkości, które są symulowane przez prymitywny model równań ( model antarktyczny o wysokiej rozdzielczości). Za pomocą tego modelu można oszacować, ile razy masa wody okrążyła Antarktydę i ile czasu spędziła w Oceanie Południowym. Okazało się, że średnio masa wody okrąża Antarktydę sześć razy, zanim po raz pierwszy dotrze do powierzchni.

Wskaźniki temperatury

Temperatury powierzchni można analizować za pomocą wskaźników zastępczych, które mogą zrekonstruować zmiany środowiskowe w ciągu ostatnich 600 lat. Te rekonstrukcje są oparte na alkenonach , lipidach błonowych i stabilnych stosunkach izotopów globigerinoides ruber . Twierdzi się, że prądy oceaniczne przenoszą te proxy daleko od miejsca pochodzenia, tworząc odchylenie w kierunku przybliżeń temperatury.

Ślady zasolenia

Wielkościami używanymi do określenia zasolenia są stosunki między pierwiastkami a wapniem i stabilnymi izotopami tlenu w otwornicach . Te stosunki izotopów można obliczyć za pomocą następującego wzoru: $\ Displaystyle \ delta ^ {X} = { \frac {^{x/y}R_{próbka}}{^{x/y}R_{referencja}}}-1}$ , gdzie y jest powszechnym izotopem, a x rzadszym izotopem. Oba wskaźniki mają dodatnią korelację w Morzu Śródziemnym , które ma silny gradient zasolenia z zachodu na wschód. Wskaźniki zasolenia są ważne dla rekonstrukcji cyrkulacji oceanicznej, ponieważ wraz z temperaturą można określić gęstość, co może zrekonstruować wzorce cyrkulacji na dużą skalę, w tym południkową cyrkulację wywracającą .

Znaczniki składników odżywczych

Wpływ Podprądu Równikowego (EUC), Podprądu Przybrzeżnego Nowej Gwinei (NGCU) i Podprądu Przybrzeżnego Nowej Irlandii zbadano za pomocą modeli w celu wyjaśnienia wysokich stężeń żelaza w Oceanie Spokojnym . Podczas El Niño dwa ostatnie prądy wzmacniają się, co zwiększa stężenie żelaza w Pacyfiku.

Plastikowy

Modele cząstek Lagrange'a pokazały, że około trzy czwarte pływających morskich tworzyw sztucznych uwolnionych z lądu trafia do wód przybrzeżnych, z najwyższym stężeniem w Azji Południowo-Wschodniej. Symulacje te są jednak przeszacowane w odniesieniu do pomiarów terenowych.

Ryba

Transport larw ryb przez prądy oceaniczne jest ważnym mechanizmem rozprzestrzeniania się , ponieważ czas ma duży wpływ na miejsce osiedlenia się larw. Pomatomus saltatrix to gatunek ryby występujący na całym świecie, a jego rozprzestrzenianie się badane jest za pomocą symulacji śledzenia cząstek. Szczególnie Prąd Wschodnioaustralijski jest ważny dla maksymalnego rozprzestrzeniania się larw.

Plankton

Plankton to ważne archiwum do rekonstrukcji przeszłych warunków powierzchni oceanów. Podczas gdy plankton tonie w osadach, może być przenoszony przez turbulentne prądy oceaniczne. Symulacje oceanów można wykorzystać do zdefiniowania obszarów dna oceanów na podstawie lokalizacji pochodzenia cząstek na powierzchni.

góry lodowe

Wpływ gór lodowych na lód morski można modelować i porównywać z obserwacjami. Kiedy topnieją góry lodowe, następuje duży przepływ świeżej wody. Wokół Antarktydy ma miejsce ujemny przepływ słodkiej wody z powodu zamarzania lodu morskiego.

Rozwój

Dostęp do najnowszej wersji OceanParcels można uzyskać za pośrednictwem GitHub . Jest stale udoskonalany, aktualizowany i rozszerzany. Projekt kodu gwarantuje, że można to zrobić bez wpływu na interfejs użytkownika. Poniżej znajduje się lista niektórych możliwych ulepszeń:

Implementacja obsługi wykorzystania siatek Arakawa D i E w interpolacji
Implementacja bardziej zaawansowanych metod interpolacji
Implementacja obsługi wykorzystania siatek nieustrukturyzowanych w procesie interpolacji
Wdrażanie nowych, wydajniejszych metod programowania
Implementacja dalszych metod całkowania numerycznego do modelowania Lagrange'a

Alternatywy dla OceanParcels

Poniższa lista zawiera kilka pakietów kodu z (częściowo) podobnymi funkcjami jak OceanParcels.

OpenDrift : Projekt Norweskiego Instytutu Meteorologicznego mający na celu opracowanie pakietów Pythona typu open source do obliczania dryfu w oceanie i atmosferze.
TRACMASS : kod Fortran 90 obliczający trajektorię cząstek za pomocą analizy oceanu Lagrange'a .
Octopus : kod Fortran obliczający katalogi cząstek Lagrange'a w oceanie na siatce C.
Connectivity-Modeling-System (CMS) : Open source fortran obliczający trajektorie cząstek w oceanie, opracowany przez Rosenstiel School of Marine and Atmospheric Science Uniwersytetu w Miami .